Correct polyhedra. Part 1. Trimerie

Introduction Statement of a question.

In the school curriculum, unfortunately, Lobachevsky’s spherical geometry and geometry are not studied. In the meantime, studying them together with Euclidean geometry allows us to understand more deeply what is happening with objects. For example, understand the connection of regular polyhedra with partitions of a sphere, partitions of the Euclidean plane and partitions of the Lobachevsky plane.
Knowledge of the geometry of spaces of constant curvature helps to rise above three dimensions and to reveal polyhedrons in spaces of dimension 4 and above. The issues of finding polyhedra, finding partitions of spaces of constant curvature, deriving the formula for the dihedral angle of a regular polyhedron in n-dimensional space are so closely intertwined that it was problematic to put all this into the title of the article. Let the center of attention be, everybody understandable, correct polyhedra, although they are not only the result of all conclusions, but also, at the same time, a tool for understanding the spaces of higher dimensions and uniformly curved spaces.

For those who do not know (have forgotten) I inform (I remind) that in the usual three-dimensional Euclidean space we have only five regular polyhedra:

1. Tetrahedron:	2. Cube:	3. Octahedron:	4. Dodecahedron:	5. Icosahedron:

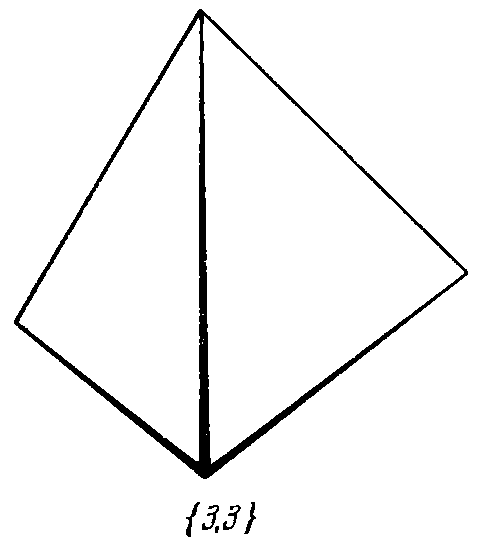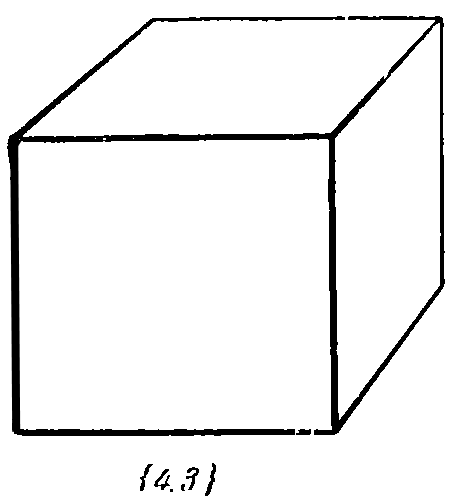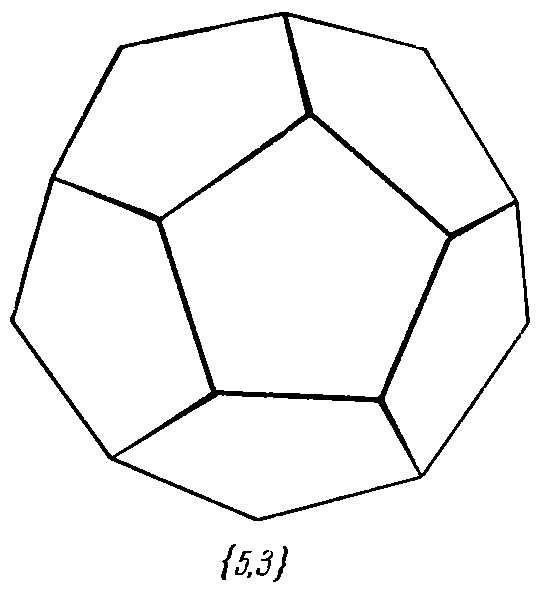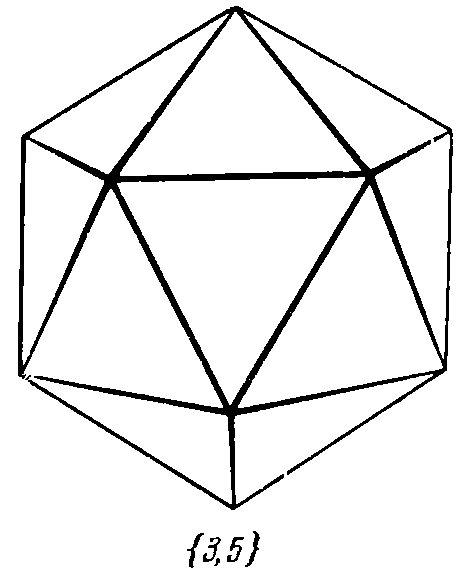In three-dimensional space, a regular polyhedron is called a convex polyhedron, in which all vertices are equal to each other, all edges are equal to each other, all faces are equal to each other and the faces are regular polygons.

A regular polygon is a convex polygon in which all sides are equal to each other and all angles are equal to each other.
')
Vertices are equal to each other means that the number of edges and the number of faces that match each vertex are the same and they fit at the same angles at each vertex.

It turns out that it is convenient to denote regular polyhedra by their Schläfli symbol {p1, p2}, which characterizes their combinatorial structure. Which means that p1 squares, converged on p2 pieces at the top. Those. By definition, p1, p2 are integers greater or equal to 3. For those who are not familiar with the concept Schläfli Symbol wrote a separate article with pictures Schläfli Symbol. Part 2.6

In such a record, our polyhedra will get the following notation:
1. Tetrahedron {3, 3},
2. Cube {4, 3},
3. Octahedron {3, 4},
4. Dodecahedron {5, 3},
5. Icosahedron {3, 5}
For example, {4, 3} - a cube has 4 coal faces, at each vertex 3 such faces converge.
The {3, 4} octahedron, on the contrary, has 3 coal faces, converge 4 at the top.
Thus, the Schläfli symbol completely defines the combinatorial structure of the polyhedron.

Why are regular polyhedra only 5? Maybe more of them?

In order to fully answer this question, you must first get an intuitive idea of ​​the geometry on the sphere and on the Lobachevsky plane. Those who have no such idea yet will try to give the necessary explanations.

Sphere

1. What is a point on a sphere? I think that everyone is intuitive. Mentally it is not difficult to imagine a point on a sphere.



2. What is a segment on a sphere? We take two points and connect them with the shortest distance on the sphere, we get an arc, if we look at the sphere from the side.



3. If we continue this segment in both directions, then it closes and we get a circle. In this case, the plane of the circle contains the center of the sphere, this follows from the fact that we have connected the two starting points with the shortest, and not arbitrary, distance. It is from the outside it looks like a circle, but in terms of spherical geometry it is straight, since it was obtained from a segment, continuing to infinity in both directions.



4. And finally, what is a triangle on a sphere? We take three points on the sphere and connect them with segments.



By analogy with a triangle, you can draw an arbitrary polygon on the sphere. For us, the property of a spherical triangle is fundamentally important, which consists in the fact that the sum of the angles of such a triangle is more than 180 degrees, to which we are accustomed in the Euclidean triangle. Moreover, the sum of the angles of two different spherical triangles is different. The larger the triangle, the more he has the sum of the angles.



Accordingly, the 4th sign of equality of triangles on a sphere appears - at three angles: two spherical triangles are equal to each other if their respective angles are equal.

For simplicity, the sphere itself is easier not to draw, then the triangle will look a bit bloated:



The sphere is also called the space of constant positive curvature. The curvature of space just leads to the fact that the shortest distance is an arc, and not the usual straight-line segment. The segment is bent.

Lobachevsky

Now that we have become acquainted with the geometry on the sphere, it will not be difficult to understand the geometry on the hyperbolic plane, discovered by the great Russian scientist Nikolai Ivanovich Lobachevsky, since everything here is similar to the sphere, only “inside out”, “vice versa”. If we conducted arcs on a sphere in circles, with the center inside the sphere, then now the arcs should be drawn in circles with the center outside the sphere.

Let's get started The Lobachevsky plane will be represented in the interpretation of Poincaré II (Jules Henri Poincare, the great French scientist), this interpretation of Lobachevsky’s geometry is also called the Poincare disc.

1. Point in the Lobachevsky plane. Point - it is in Africa point.



2. A segment on the Lobachevsky plane. We connect two points by a line according to the shortest distance in the sense of the Lobachevsky plane.



The shortest distance is constructed as follows:



It is necessary to draw a circle orthogonal to the Poincaré disk, through the given two points (Z and V in the figure). The center of this circle will always be outside the disk. The arc connecting the original two points will be the shortest distance in the sense of the Lobachevsky plane.

3. Removing the auxiliary arcs, we obtain the straight line E1 - H1 in the Lobachevsky plane.



The points E1, H1 “lie” at infinity of the Lobachevsky plane, in general, the edge of the Poincaré disk is all the infinitely distant points of the Lobachevsky plane.

4. And finally, what is a triangle in the Lobachevsky plane? Take three points and connect them with segments.



By analogy with a triangle, you can draw an arbitrary polygon on the Lobachevsky plane. For us, the property of a hyperbolic triangle is of fundamental importance, which consists in the fact that the sum of the angles of such a triangle is always less than 180 degrees, to which we are accustomed in the Euclidean triangle. Moreover, the sum of the angles of two different hyperbolic triangles is different. The larger the triangle in area, the less it has the sum of the angles.



Accordingly, here too, the 4th sign of equality of hyperbolic triangles takes place - at three angles: two hyperbolic triangles are equal to each other, if their respective angles are equal.

For simplicity, the Poincare disc itself can sometimes not be drawn, then the triangle will look a bit “shrunken”, “deflated”:



The Lobachevsky plane (and generally the Lobachevsky space of any dimension) is also called the space of constant NEGATIVE curvature. The curvature of space just leads to the fact that the shortest distance is an arc, and not the usual straight-line segment. The segment is bent.

Correct partitions of a two-dimensional Sphere and regular three-dimensional polyhedra

Everything said about the sphere and the Lobachevsky plane relates to two-dimensional, i.e. the surface of the sphere is two-dimensional. What does this have to do with the trimeria indicated in the title of the article? It turns out that each three-dimensional regular Euclidean polyhedron is in one-to-one correspondence with its own partition of a two-dimensional sphere. This is best seen in the figure:



To get a partition of a sphere from a regular polyhedron, you need to describe a sphere around a polyhedron. The vertices of the polyhedron will be on the surface of the sphere, connecting these points by segments on the sphere (arcs), we obtain a partition of the two-dimensional sphere into regular spherical polygons. For example, a video demonstration has been made of how an icosahedron corresponds to the division of a sphere into spherical triangles and vice versa, as a division of a sphere into spherical triangles converging five pieces at the top corresponds to an icosahedron.



In order to construct a polyhedron by dividing the sphere, the corresponding arcs of the vertex of the splitting need to be connected by usual, straight-line, Euclidean segments.

Accordingly, the Schläfli symbol of the icosahedron {3, 5} - triangles converging five at the top, defines not only the structure of this polyhedron, but also the structure of the partition of the two-dimensional sphere. Similarly to other polyhedra, their Schläfli symbols define the structure of the corresponding partitions. Moreover, partitions of the Euclidean plane and the Lobachevsky plane into regular polygons can also be defined by the Schläfli symbol. For example, {4, 4} - quadrangles converging in four - this is all the usual notebook in the cell, i.e. it is a partition of the Euclidean plane into squares. Are there any other tilings of the Euclidean plane? We will see further.

Construction of partitions of a two-dimensional sphere, the Euclidean plane and the Lobachevsky plane

To construct partitions of two-dimensional spaces of constant curvature (this is the common name of these three spaces), we need elementary school geometry and the knowledge that the sum of the angles of a spherical triangle is more than 180 degrees (more than Pi), that the sum of the angles of a hyperbolic triangle is less than 180 degrees (less than Pi) and What is the Schläfli symbol? About all this has already been said above.

So, take an arbitrary Schläfli symbol {p1, p2}, it defines a partition of one of the three spaces of constant curvature (for a plane this is true, for spaces of higher dimensions, the situation is more complicated, but nothing prevents us from investigating all combinations of a character).



Consider a regular p1 square, draw the segments connecting its center and its vertices. We obtain p1 pieces of an isosceles triangle (only one such triangle is shown in the figure). We denote the sum of the angles of each of these triangles by t and express t by pi and the coefficient lamda.



Then if lamda = 1, then the Euclidean triangle, i.e. is in the Euclidean plane, if lamda is in the interval (1, 3), then this means that the sum of the angles is greater than pi and that means this triangle is spherical (it’s not hard to imagine that increasing the spherical triangle in the limit yields a circle with three points on it, for each point, the angle of the triangle is obtained equal to pi, and in the sum of 3 * pi. This explains the upper limit of the interval = 3). If lamda is in the interval (0, 1), then the triangle is hyperbolic, since the sum of the angles is less than pi (that is, less than 180 degrees). In short, this can be written as:



It is not difficult to calculate that:



On the other hand, for the convergence at the vertex p2 of the pieces (i.e. an integer) of the same polygons, it is necessary that



Equating the expressions for 2 * betta, found from the convergence condition and from the polygon:



We got an equation that shows which of the three spaces is broken by the figure given by its symbol Schläfli {p1, p2}. To solve this equation, we must remember that p1, p2 are integers greater or equal to 3. This, so to speak, follows from their physical meaning, since these are p1 squares (at least 3 corners) converging in p2 pieces at the vertex (also not less than 3, otherwise it will not be a vertex).

The solution of this equation consists in the enumeration of all possible values ​​for p1, p2 greater or equal to 3 and the calculation of the value of lamda. If it turns out to be equal to 1, then {p1, p2} splits the Euclidean plane, if more than 1 but less than 3, then this is a partition of the Sphere, if from 0 to 1, then this is a partition of the Lobachevsky plane. All these calculations are conveniently tabulated.



Whence it is clear that:
1. The sphere corresponds to only 5 solutions, when the lamda is greater than 1 and less than 3, they are highlighted in green in the table. These are: {3, 3} - tetrahedron, {3, 4} - octahedron, {3, 5} - icosahedron, {4, 3} - cube, {5, 3} - dodecahedron. Their pictures were presented at the beginning of the article.
2. The splitting of the Euclidean plane corresponds to only three solutions, when lamda = 1, they are highlighted in blue in the table. Here’s what these splits look like.





3. Finally, all other combinations {p1, p2} correspond to partitions of the Lobachevsky plane, respectively, such partitions have an infinite (countable) number. It remains only to illustrate some of them, for example.

{3, 7}



{4, 5}



{4, 6}



{4, 7}



{5, 4}



{5, 5}



{5, 6}



{5, 7}



{6, 4}

Results

Thus, there are only 5 regular polyhedra, they correspond to five partitions of a two-dimensional sphere, only 3 Euclidean plane partitions, and Lobachevsky plane partitions are countable.
What application of this knowledge?

There are people who are directly interested in partitions of the sphere: dxdy.ru/topic62800.html ,
There are articles on Habré ( here ), where also interpretations of Lobachevsky’s geometry are considered. This article may help someone better understand and get acquainted with the geometry of Lobachevsky.

The knowledge of polyhedra also helps to answer the question: how many footballs have regular hexagons and how many pentagons. Knowing that a soccer ball is a truncated icosahedron, you can immediately answer this question: there are as many pentagons as the icosahedron vertices, as many hexagons as the icosahedron faces, 12 pentagons, and 20 hexagons.

Yes, I would like to tell you more about the combinatorial formula for calculating the number of vertices, edges and faces of these five regular polyhedra, but this is the next time. And somehow it turned out to be quite complicated, although I was counting on the school level of knowledge of the readers.

Also in the next article, if readers are interested, I plan to show how this approach is generalized to spaces of higher dimensions.

For me personally, knowledge of partitions allows us to understand the structure of these spaces, this is especially true in dimensions above 3.

If you have a little three-dimensional space, you understand this publication and you want to climb higher, in dimension, then “go to the next level” :)
References:
Correct polyhedra. Part 1. Trimerie
Correct polyhedra. Part 2. Foursome
Correct polyhedra. Part 2.5 (auxiliary)
Schläfli symbol. Part 2.6