Factorization and encryption on the elliptic curve
The problem of factoring composite natural numbers (snnch) for many centuries has kept the attention of specialists in various theoretical (scientific) and applied fields such as numerical systems, computational mathematics and technology, number theory, information security, cryptography, and others, and forces them to make considerable efforts. to its positive and successful solution. Nevertheless, the problem today is far from its closure, completion. The author offers for consideration and seeks to give the reader an idea of the existing approaches to solving the problem, which have already become a kind of classic, to bring criticism and express approval of the remarkable finds.
The paper presents one of the well-known approaches to solving the problem of the factorization of large numbers (SFSH), using the mathematics of elliptic curves (EC). About this mathematics, and more precisely about the technique of calculations, I will quote the authors of [1] “The technique currently used in studying EC is one of the most sophisticated in all mathematics. We hope that the elementary approach of the present work will induce the reader to further study this lively and fascinating branch of the theory of numbers. There is a lot that needs to be learned, and a lot of work that still needs to be done. „
It is convenient to build a theoretical presentation of the material, accompanied by a finite numerical example and detailed digressions and comments, which will allow, without jumping over different parts of the work, and successfully delve into the essence of the presented material. It is clear that the task is not simple and requires a certain preliminary preparation from the reader, but such is the specificity of “Habra” - the presence of readers of different levels of training.
First we give several necessary definitions of higher algebra.
An algebraic (finite) group is a set of elements (numbers, polynomials, matrices, etc.) over which one operation is given. Depending on the nature of the elements (matrices, substitutions, deductions modulo N), the operations may differ, but their names, as a rule, are always the same: addition and multiplication. In the case of groups of residues modulo N, the set of elements of a group can be whole or even natural zero-filled numbers from 0 to N - 1. The only operation of the group by purpose can be addition (+), and then the group is called additive, or multiplication (•), and the group is called multiplicative. Both group operations have similar properties (described extensively in educational literature): associativity, closure, the presence of neutral and opposite (inverse) elements, while maintaining the result of the operation in case of changing operands in places - commutativity. We explain the property of closure. The set of elements that make up a finite group, of course and constantly. The results of the operation are always elements from the original set. Among the elements of the group, only one is a neutral element, and each element has its opposite ( a -1 ) (or opposite ( -a )). Operation on elements does not bring the result beyond the limits of the initial set of elements of the group. The fact is that in the groups of residues modulo N, the addition or multiplication operations are not ordinary, but modular, that is, the group is given the number N, called the module of the group, and all the results are divided into it. Such a division, as a rule, is performed with the remainder and it is the remainder that is taken as the final result of the operation.
Mathematician Cayley proposed to characterize the set of results of such operations by tables that received his name (Cayley's tables), an addition table for an additive group, and a multiplication table for a multiplicative one.
The order of a group is the number of its elements. Each individual element in the group is also characterized by its order.
The order (period) of an element in a group is the smallest positive number (the multiplicity k of the element) in the operation, in which the result of the operation turns into a neutral element.
a + a + ... + a = ka = 0 or a ∙ a ∙ a ∙ ... ∙ a = a k = 1 .
The element period is a multiple of the group order, i.e. divides the order of the group entirely.
An algebraic finite simple field of residues modulo a simple N is the set (k, GF (p), Fp) of elements (numbers from 0 to N - 1), over which two addition operations (+) and multiplication (•) are given. Module N, according to which field elements are formed, must necessarily be a prime number. Among the elements there are necessarily opposite (-a) to each element and one neutral (0) in addition, inverse ( a -1 ) to each element and one neutral (1) in multiplication. The field is formed in accordance with the operations allowed in it (+) and (•) by two corresponding groups.
In addition to finite number simple fields in various theories (coding, cryptography, algebra, geometry, etc.), the fields of polynomials are used.
Such fields GF (p n ) appear as the result of extending a certain degree of n simple fields GF (p).
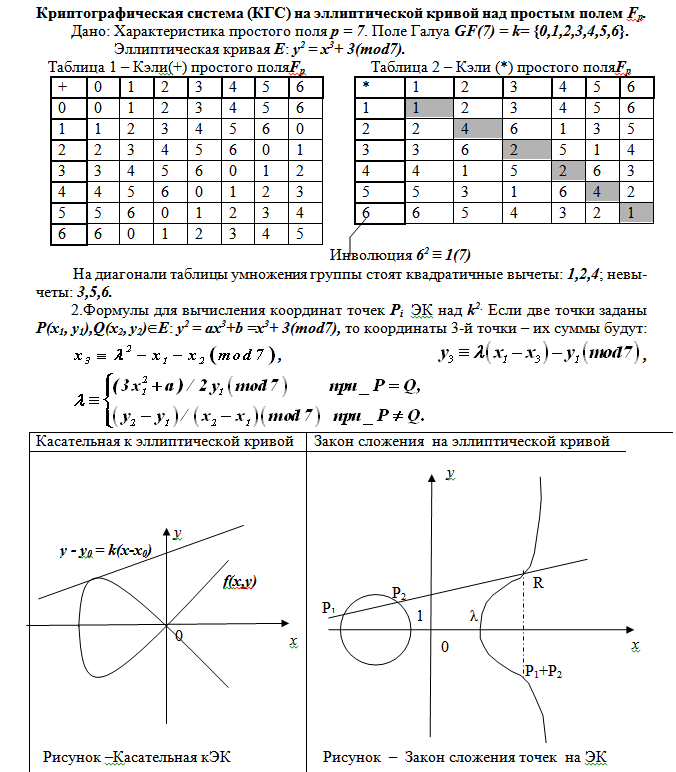
The field extension is the field GF (p n ), containing this field GF (p) as a subfield, which is written as K / k, where k = GF (p), K = GF (p n ) is the extension of the field k. The elements of the extension field K are all elements (numbers) of a simple field k and all polynomials of degree not exceeding n - 1. Examples of field groups and the results of both operations in groups for example GF (7) fields of addition and multiplication are the numerical tables 1 and 2 placed below
Algebraic numerical finite residue ring modulo N (denoted Z N ) is the set of elements (numbers from 0 to N - 1), over which two addition operations (+) and multiplication (•) are given. The module N, according to which ring elements are formed, must be a composite (not prime) number. If the module is made a simple number (irreducible polynomial), then the ring is transformed into a simple field (the field of polynomials). Among the ring elements there are necessarily opposite (-a) to each element and neutral (0) in addition, but the inverse element ( a -1 ) does not exist for each element and the neutral element (1) by multiplication in the ring may be missing. If the reduction module is a reducible polynomial of degree n, then a ring of polynomials arises, whose elements are actually the same elements as in the field of polynomials, but operations on polynomials are performed not in the same way as in the extension field. A similar situation with elements arises for vector spaces - they are the same there as in the field and in the ring. Operations are significantly different. The results of the operation of multiplying the elements of the field and the same elements of the ring or vector space will differ. For our presentation, it is essential that not all elements have rings in the multiplicative group of the ring.
Example 1 Let a simple modulo two residue field be given — a binary field GF (2) = {0,1}. We construct the extension field of a degree, for example, n = 6, which is denoted as GF (2 6 ). This field is formed by the numbers 0, 1 and all possible polynomials of degree not exceeding 5. When actions are performed with polynomials in the multiplicative field group, the degree of the result (the product of polynomials) degd (x) can exceed the exponent n = 5. At the same time, the condition of closure of the set elements of the multiplicative group is violated. To return the result to the field - to make it an element of the field, the result of the product is divided into a specially selected polynomial (for example, f (x) = x 6 + x + 1) of the degree of equal extension, i.e. n = 6. Such a polynomial essentially forms a field and must not have roots in a simple field, it is called an irreducible polynomial, that is, it does not decompose into factors in a field.
Say the results of field operations are given modulo an irreducible polynomial. In addition, all coefficients of polynomials in a field belong to a simple field and are modulo a simple field (a prime number). Thus, the results of operations in a field are given in double modulus, which is sometimes denoted as d (x) (moddp, f (x)), where p is a prime number that forms a simple field and f (x) is an irreducible polynomial of degree of equal degree extensions of a simple field.
')
ELEMENTS OF THE THEORY OF ELLIPTIC CURVE
It is convenient to perform modeling of many phenomena of reality, in particular, mathematical, involving algebraic structures: groups, fields, rings, algebras, etc. Those properties that are already well studied for certain structures are inherited by objects that are modeled using such structures. This saves time and effort, as well as other resources. One example of using the well-known properties of finite additive groups is the development of algorithms for solving SFCPs, digital signature algorithms, and / or encryption of documents (messages) in which non-ordinary groups are involved. The algorithms use points of an algebraic curve defined over finite structures (field, ring), reduced (calculations are modulo the characteristics of N) called the Weierstrass elliptic curve (EC), whose integer (rational) points form an additive group, i.e. they can be summed up in any order, while receiving new points from this group. Under certain conditions imposed on a curve, the set of such points is closed and of course, although the order of the group can be very large. The curve itself is flat its coefficients a and b; EC points (x, y) are described in terms of two x and y variables whose values belong to the finite simple Galois field GF (p) (but may also belong to the extended field GF (p n ), as in some standards of electronic digital signature). Thus, the algorithms use the Cartesian product of the field GF (p) xGF (p).
The operation of adding points to an EK is a special operation (+), the final step of which is taking the result modulo N simple or (for a ring) composite. In the case of a composite module, the EC is not set above the field, but above the ring, which significantly changes the properties of the objects under consideration, preserving the main ones.
Consider the most basic information from the theory and arithmetic of elliptic curves. It is necessary to clarify a number of points. The task of EC, the semantic meaning of the parameters of EC, the set of integer points and the possibility of their addition among themselves. The operation of adding points. This information and their understanding are necessary for an accessible presentation of the factorization algorithm for natural (integer) numbers, which has long been known to cryptology specialists by H. Lenstra's publications from 1987 and later improvements by R. Montgomery 1992 [2, 4, 5, 6, 7, ten ]. To define an elliptic curve E a, b (F p ) over a field, at first, the field is defined by the characteristic of a finite field — a prime number N or p> 3. To set the coefficients a and b of an elliptic curve E (a, b) defined over a finite simple field Fp, one can use the approach from the national standard. ( GOST ).
Thus, the elliptic curve E a, b (F p ) is the set {(x, y)} of pairs of numbers , elements of the field x, y ∊ Fp satisfying the relation y 2 ≡ x 3 + ax + b (modp), where a , b∊Fr. In E a, b (F p ) the discriminant is -4 3 + 27b 2 ≢ 0 (modp) and is not comparable with zero modulo p. It is more correct to say this is the group of points of EC, and not the curve itself. But such a replacement of concepts in something simplifies the presentation.
The EC coefficients a and b are determined by the relations a ≡ 3k (modp); b 3k (modp);
where k ≡ J (E) (1728 - J (E)) -1 (modp); J (E) ≡ 1728 ∙ 4a 3 (4a 3 + 27b 2 ) -1 (modp) EC invariant; J (E) ∨ 0∨1728.
Pairs of numbers (x, y) that satisfy the EC equation are called its points, denoted by Q (x, y), and x and y are the coordinates of the point. As a neutral element, a group of EC points includes a special point (O), a point remote to infinity (∞), its coordinates are usually not calculated. The operation of addition (+) is introduced on the set of all integer points of EC. For two arbitrary points Q 1 (x 1 , y 1 ) and Q 2 (x 2 , y 2 ) of the curve E (a, b), the summation is performed using different formulas depending on the coordinate relation of the points.
If both coordinates are equal, the points x 1 = x 2 , y 1 = y 2 ≠ 0, we have a doubling or the sum of one point with itself. The resulting point Q 3 (x 3 , y 3 ) gets the coordinates calculated by the formulas
x 3 ≡ λ 2 - 2x 1 (modp);
y 3 ≡ λ (x 1 - x 3 ) - y 1 (modp),
where λ ≡ (3x 1 2 + a) (2 1 ) -1 (modp).
At x 1 ≠ x 2 the sum of the points Q 1 (x 1 , y 1 ) and Q 2 (x 2 , y 2 ) is the point Q 3 (x 3 , y 3 ), which receives the coordinates calculated by the formulas
x 3 ≡ λ 2 - x 1 - x 2 (modp);
y 3 ≡ λ (x 1 -x 3 ) - y 1 (modp),
where λ ≡ (y 2 - y 1 ) (x 2 - x 1 ) -1 (modp).
For x 1 = x 2 , y 2 = - y 1 (modp), the points lie on the vertical line intersecting the EC in them. This straight line intersects the third point (O) EC, which is removed at infinity. The sum of the points Q 1 (x 1 , y 1 ) and Q 2 (x 2 , y 2 ) is called the neutral element (zero point O) of the group, whose coordinates are not determined. Summation with this point of any other point does not change this other and gives the result Q + O = O + Q = Q.
The point Q has the multiplicity k or is simply called the multiple point E (a, b) if for some point P∊E (a, b) the equality Q = P + P + ... + P = kP holds. If for point it is true + + ... + = kP = , then k is the order of point R.
The operation of summation of all integer points E (a, b) together with the zero point O (neutral element) generates a finite (commutative) additive (Abelian) group of order q, where q ≠ p. For this order, the Has + relation established by p + 1 - 2√r <q <p + 1 + 2√r is valid.
A SIMPLE CRYPTOGRAPHIC SYSTEM ON ELLIPTIC CURVES
In the data exchange network for all subscribers, the total reduced elliptic curve E a, b (F p ) over the field F p and the generating point P = (x, y) on it are set. Each subscriber, using the points of the additive group of this EC, forms its public and private keys. Below in example 2, a simple version of a cryptographic system (CGS) with the ability to encrypt / decrypt messages with elements of a group of points of EC is considered. Understanding the basics of the theory of elliptic curves and related issues opens up the possibility of using a rich arsenal of their tools in order to increase the level of information systems security and prevent possible attacks on them.
The basic rules of the protocol. The sender encrypts his message with the recipient's public key, the recipient uses the private key to decrypt the received encrypted messages. The public keys of all subscribers are accessible to all, the private (private) keys are kept secret from all.
Encryption : Let the sender B send to the recipient A a message in the form of a source text (IT) of one three-letter word “DOM”
These characters must be converted into a digital (binary) form, for example, an ASCII code.
IT = {IT1 = D = E4 = 1110 1000, IT2 = O = EE = 1110 1110, IT3 = M = EC = 1110 1100}
To character-encrypt a message to subscriber B, subscriber A's public key is required. Subscriber A generates this key and publishes it as publicly available on the communications network.
Public key A: point generator group EK Q = P5 = (3.3). The choice of this point is quite arbitrary. Further, A generates a random number a = 3 which for subscriber A is a private (sometimes called a secret key) key. Point Q is multiplied by the private key. It turns out the point N = aQ = 3Q = 3P5 = P11 = (6,3). the final public key is: Q, N.
The sender B generates his random number b = 2 and multiplies both points of the public key Q and N by b = 2: gets the points R = bQ = P4 = (2,5); S = bN = baQ = P8 = (4, 5).
Then the coordinates of the point S = (4, 5) are converted to the binary representation S = P8 = (4, 5) = (0000 0100, 0000 0101). The characters of the message and the xs coordinate are then converted into cipher text (PC). The simplest way to convert message text with EXOR operation
= {1 = 1110 1100; 2 = 1110 1010; 3 = 1110 1000}.
Sender B sends to recipient A a point EK R and an encrypted message.
Decryption : performs side A - the recipient of the message. The point R of the curve is multiplied by the personal (secret) key (a) of subscriber A: aR = abQ = S = 3P4 = P8 = (4,5), which also gives the point S = P8 = (4,5). Subscriber A then performs decryption, obtaining the source text of the IT.
Here is a very simplified version of encrypted messaging, when both subscribers use the same shared key. In fact, each symbol of the source text can be represented by an EC point or a coordinate of such a point. In the latter case, a group operation is used to convert the points of EC modulo.
Example 2
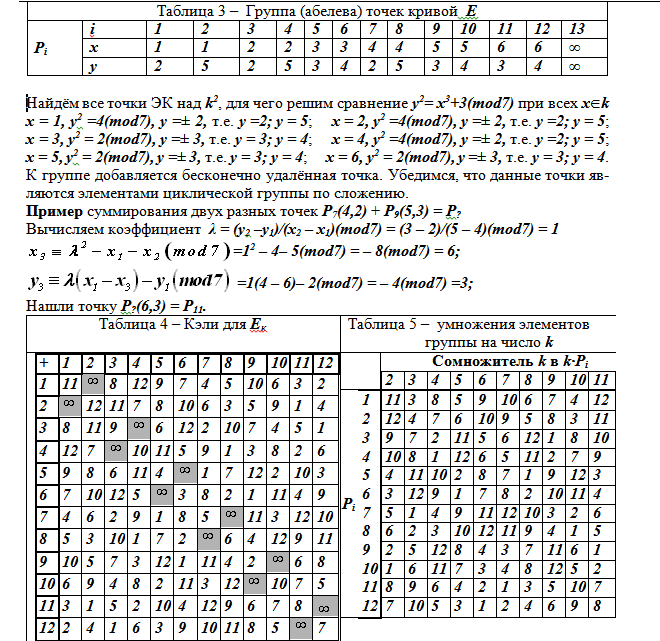
k is the number of terms equal to the point Pi of the corresponding line. The cells of tables 4 and 5 contain the numbers i of points of Pi from table 3, where all 13 points of the final additive group of an elliptic curve y 2 ≡ x 3 + 3 (mod7) are presented
ALGORITHM OF NUMBER OF FACTORIZATION
This probabilistic algorithm displays the main features of its presentation in [3, 7, 9].
1 Choose the number N and the number 1 <a, x, y <N;
2 we assume b = y 2 - x 3 - ah (modN). Then for EC y 2 ≡ x 3 + ah + b (moN), where a, b, x, y ∊ Fp choose the point P = (x, y);
3 Find d = NOD (N, 4 3 + 27b 2 ), if 1 <d <N, then d | N and the problem is solved, if d = 1, then go to the next step;
4 Choose the number k = LCM (2, 3, ..., M), M is a natural number;
5 Calculate multiple points kP on EC, k = 2,3, ..;
6 Calculate d = NOD (N, x k - x k-1 ),
if 1 <d <N, then d | N problem solved, divider N found,
if d = 1, then either go to step 4 and increase k, or go back to step 1 and select the parameters of the new curve,
if d = 1, then go to step 4 and decrease k.
For factorization, a compound odd number n is specified. An integer k is chosen equal to the product of the degrees of small primes with bounded exponents:
k = 2 d2 3 d3 5 d5 ... r dr . Here 2, 3, 5, ..., r are some of the first prime numbers, and d2, d3, d5, ... dr are small positive numbers. After that, a k - 1 is calculated modulo n and then (n, and k - 1), which requires 2 ℓog 2 (2kn) operations to be calculated. k n .
(n, k — 1) ≠ n, n. n , , . (n, k -1) = n, . (n, k — 1) = 1, k . [3] :
((2 +(1))ℓogpℓogℓogp) 1/2 ℓog 2 N , — N.
A specific numerical example of a factorization of a number is given below with explanations of individual computational elements.
Example 3 . This example shows the possibility of solving the problem of number factorization (the composite module of a numerical residue ring) using EC. The algorithm is based on the multiple summation of the EC point with itself, i.e. calculating the additive order of the EC point. This order divides the order of the group of points of the EC. In this case, it is possible that the solution of the factorization problem appears earlier than the order of the point is found in the process of calculating multiple points. Finding the sum of two points requires calculating the coefficient λ, for which the extended GCD (N, x 2 - x 1 ) Euclidean algorithm is involved .
d = >1, d ≠ N, N . N = 455839= 599•761. : 2 ≡ 3 + 5 -5(modN), = b = 5∊ ZN (, b) -4 3 + 27b 2≢ 0 (modN) is not comparable to zero modulo N. A rational point P = (1,1) on the EC is also given. We will repeatedly summarize this point with us. Sooner or later, such summation will lead to a result — a neutral element — a point (0), since each element of the algebraic structure has a period. Of course, this summation is a very lengthy process, but the algorithm, it turns out, can often lead to a solution at the intermediate step of the calculations. Therefore, for large numbers, we will first find a small sum of points, for example, 10! = 2 8 • 3 4 • 5 2 • 7 = 3628800 • and with their deficiency increase the number.
Let's start with a double point P 2 = 2! = 1 • 2 • . Find for P 2 the value of λ≡ (3x 1 2 + )(2 1 ) -1 (modN) = (3•1 2 + 5)/(2•1)≡4(modN) 2
2 ≡ λ 2 — 2 1 (modN) = 4 2 — 2•1(modN) = 14;
2 ≡ λ( 1 — 2 ) — 1 (modN) = 4(1 — 14) — 1(modN) = -53(modN) => -53(modN) = 455839-53 = 455786.
2 , 2 ≠ 0, 2 , . , 2 = ( 2 , 2 ) .
2 2 = (-53) 2 = 2809 = 14 3 + 5•14 — 5 = 2744+70 — 5 = 2809(modN), 2 ∊ .
3 = 3! = 1•2•3•=6 =2+ 4. 2 2 = 4, 2 . 2 2
λ ≡ (3 2 2 + )(2 2 ) -1 (modN) = (3•196 + 5)/(2(-53)) = — 593/106 = 322522(modN)
2 2
2 ≡ λ 2 — 2 1 (modN) = 259851;
2 ≡ λ( 1 — 2 ) — 1 (modN) = 116255(modN).
In calculating the coefficient λ = 322522, arithmetic of the field, ring, and EC is used. The fact is that in algebraic structures there is no division operation by number. When it appears in formulas, it must be eliminated, which is done by multiplying by the inverse element that stands in the denominator of the formula. The definition of such an inverse element is possible if the element is reversible (in the finite residue ring, not all elements have inverses). For the expression λ = - 593/106 (mod455839) we have just such a case, i.e. for element 106, it is necessary to determine the element inverse to it in the finite ring modulo N. We will show how this can be done in our example; an extended search algorithm is used to find the greatest common divisor of two numbers: the module 455839 and the denominator λ of the number 106:
455839 = 4300 • 106 + 39;
106 = 2 • 39 + 28;
39 = 1•28 + 11;
28 = 2•11 + 6;
11 = 1•6 + 5;
6 = 1•5 + 1. , (455839, 106) = 1. 106;
1= 6 — 5 = 2•6 — 11 = 2•28 — 5•11 = 7•28 — 5•39 = 81707•106 — 19•455839 => 81707•106 — 19•455839 ≡ 1(mod455839) =>81707•106 ≡ 1(mod455839) , , 1/106 ≡ 81707(mod455839).
λ = — 593/106(mod455839) => λ = — 593•81707(mod455839) = 322522.
3 2 4. λ
3 ≡ λ 2 - 1 — 2 (modN) = 195045;
3 ≡ λ( 1 — 3 ) — 2 (modN) = 123227(modN).
4 = 4! , 5 = 5! … 8 = 8! , λ 599, d= (455839, 599) d = 599, .. N, . N/599 = 761. .
List of used sources
[1] Ayerlend K., Rozen M. A classic introduction to modern number theory. - M .: Mir, 1987. -416s.
[2] Bolotov A.A. et al. An elementary introduction to elliptic cryptography. Algebras. and algorithmic principles.-M .: KomKniga, 2006.-328 p.
[3] Vasilenko O.N. Number-theoretic algorithms in cryptography. - M .: MTSNMO, 2003.-328 p.
[4] Zhdanov ON, Chalkin V.A. Elliptic curves. Fundamentals of the theory and cryptographic applications. -M .: KN. House "LIBROKOM", 2012.-200s.
[5] Ishmukhametov S.T. Factorization methods for natural numbers .- Kazan: Kazan.un-t, 2001.-190 p. (Http://www.ksu.ru/f9/bibl/Monograph_ishm,pdf)
[6] E. Knapp. Elliptic curves .- M .: Factorial-press, 2004.-488 p.
[7] Koblitz NA Course in Namber theory and cryptography. Springer-Verlag, 1987.
[8] Lenstra HW (1987) Factoring integer with elliptic curves. Ann.of Math.126(2),649-673.(http://www.ams.org/mathscinet-getitem?mr=89g:11125).
[9] .. . .--: - - .,2003.-192.
[10] .. .- .: , 1991. — 368 .
The paper presents one of the well-known approaches to solving the problem of the factorization of large numbers (SFSH), using the mathematics of elliptic curves (EC). About this mathematics, and more precisely about the technique of calculations, I will quote the authors of [1] “The technique currently used in studying EC is one of the most sophisticated in all mathematics. We hope that the elementary approach of the present work will induce the reader to further study this lively and fascinating branch of the theory of numbers. There is a lot that needs to be learned, and a lot of work that still needs to be done. „
It is convenient to build a theoretical presentation of the material, accompanied by a finite numerical example and detailed digressions and comments, which will allow, without jumping over different parts of the work, and successfully delve into the essence of the presented material. It is clear that the task is not simple and requires a certain preliminary preparation from the reader, but such is the specificity of “Habra” - the presence of readers of different levels of training.
First we give several necessary definitions of higher algebra.
An algebraic (finite) group is a set of elements (numbers, polynomials, matrices, etc.) over which one operation is given. Depending on the nature of the elements (matrices, substitutions, deductions modulo N), the operations may differ, but their names, as a rule, are always the same: addition and multiplication. In the case of groups of residues modulo N, the set of elements of a group can be whole or even natural zero-filled numbers from 0 to N - 1. The only operation of the group by purpose can be addition (+), and then the group is called additive, or multiplication (•), and the group is called multiplicative. Both group operations have similar properties (described extensively in educational literature): associativity, closure, the presence of neutral and opposite (inverse) elements, while maintaining the result of the operation in case of changing operands in places - commutativity. We explain the property of closure. The set of elements that make up a finite group, of course and constantly. The results of the operation are always elements from the original set. Among the elements of the group, only one is a neutral element, and each element has its opposite ( a -1 ) (or opposite ( -a )). Operation on elements does not bring the result beyond the limits of the initial set of elements of the group. The fact is that in the groups of residues modulo N, the addition or multiplication operations are not ordinary, but modular, that is, the group is given the number N, called the module of the group, and all the results are divided into it. Such a division, as a rule, is performed with the remainder and it is the remainder that is taken as the final result of the operation.
Mathematician Cayley proposed to characterize the set of results of such operations by tables that received his name (Cayley's tables), an addition table for an additive group, and a multiplication table for a multiplicative one.
The order of a group is the number of its elements. Each individual element in the group is also characterized by its order.
The order (period) of an element in a group is the smallest positive number (the multiplicity k of the element) in the operation, in which the result of the operation turns into a neutral element.
a + a + ... + a = ka = 0 or a ∙ a ∙ a ∙ ... ∙ a = a k = 1 .
The element period is a multiple of the group order, i.e. divides the order of the group entirely.
An algebraic finite simple field of residues modulo a simple N is the set (k, GF (p), Fp) of elements (numbers from 0 to N - 1), over which two addition operations (+) and multiplication (•) are given. Module N, according to which field elements are formed, must necessarily be a prime number. Among the elements there are necessarily opposite (-a) to each element and one neutral (0) in addition, inverse ( a -1 ) to each element and one neutral (1) in multiplication. The field is formed in accordance with the operations allowed in it (+) and (•) by two corresponding groups.
In addition to finite number simple fields in various theories (coding, cryptography, algebra, geometry, etc.), the fields of polynomials are used.
Such fields GF (p n ) appear as the result of extending a certain degree of n simple fields GF (p).
The field extension is the field GF (p n ), containing this field GF (p) as a subfield, which is written as K / k, where k = GF (p), K = GF (p n ) is the extension of the field k. The elements of the extension field K are all elements (numbers) of a simple field k and all polynomials of degree not exceeding n - 1. Examples of field groups and the results of both operations in groups for example GF (7) fields of addition and multiplication are the numerical tables 1 and 2 placed below
Algebraic numerical finite residue ring modulo N (denoted Z N ) is the set of elements (numbers from 0 to N - 1), over which two addition operations (+) and multiplication (•) are given. The module N, according to which ring elements are formed, must be a composite (not prime) number. If the module is made a simple number (irreducible polynomial), then the ring is transformed into a simple field (the field of polynomials). Among the ring elements there are necessarily opposite (-a) to each element and neutral (0) in addition, but the inverse element ( a -1 ) does not exist for each element and the neutral element (1) by multiplication in the ring may be missing. If the reduction module is a reducible polynomial of degree n, then a ring of polynomials arises, whose elements are actually the same elements as in the field of polynomials, but operations on polynomials are performed not in the same way as in the extension field. A similar situation with elements arises for vector spaces - they are the same there as in the field and in the ring. Operations are significantly different. The results of the operation of multiplying the elements of the field and the same elements of the ring or vector space will differ. For our presentation, it is essential that not all elements have rings in the multiplicative group of the ring.
Example 1 Let a simple modulo two residue field be given — a binary field GF (2) = {0,1}. We construct the extension field of a degree, for example, n = 6, which is denoted as GF (2 6 ). This field is formed by the numbers 0, 1 and all possible polynomials of degree not exceeding 5. When actions are performed with polynomials in the multiplicative field group, the degree of the result (the product of polynomials) degd (x) can exceed the exponent n = 5. At the same time, the condition of closure of the set elements of the multiplicative group is violated. To return the result to the field - to make it an element of the field, the result of the product is divided into a specially selected polynomial (for example, f (x) = x 6 + x + 1) of the degree of equal extension, i.e. n = 6. Such a polynomial essentially forms a field and must not have roots in a simple field, it is called an irreducible polynomial, that is, it does not decompose into factors in a field.
Say the results of field operations are given modulo an irreducible polynomial. In addition, all coefficients of polynomials in a field belong to a simple field and are modulo a simple field (a prime number). Thus, the results of operations in a field are given in double modulus, which is sometimes denoted as d (x) (moddp, f (x)), where p is a prime number that forms a simple field and f (x) is an irreducible polynomial of degree of equal degree extensions of a simple field.
')
ELEMENTS OF THE THEORY OF ELLIPTIC CURVE
It is convenient to perform modeling of many phenomena of reality, in particular, mathematical, involving algebraic structures: groups, fields, rings, algebras, etc. Those properties that are already well studied for certain structures are inherited by objects that are modeled using such structures. This saves time and effort, as well as other resources. One example of using the well-known properties of finite additive groups is the development of algorithms for solving SFCPs, digital signature algorithms, and / or encryption of documents (messages) in which non-ordinary groups are involved. The algorithms use points of an algebraic curve defined over finite structures (field, ring), reduced (calculations are modulo the characteristics of N) called the Weierstrass elliptic curve (EC), whose integer (rational) points form an additive group, i.e. they can be summed up in any order, while receiving new points from this group. Under certain conditions imposed on a curve, the set of such points is closed and of course, although the order of the group can be very large. The curve itself is flat its coefficients a and b; EC points (x, y) are described in terms of two x and y variables whose values belong to the finite simple Galois field GF (p) (but may also belong to the extended field GF (p n ), as in some standards of electronic digital signature). Thus, the algorithms use the Cartesian product of the field GF (p) xGF (p).
The operation of adding points to an EK is a special operation (+), the final step of which is taking the result modulo N simple or (for a ring) composite. In the case of a composite module, the EC is not set above the field, but above the ring, which significantly changes the properties of the objects under consideration, preserving the main ones.
Consider the most basic information from the theory and arithmetic of elliptic curves. It is necessary to clarify a number of points. The task of EC, the semantic meaning of the parameters of EC, the set of integer points and the possibility of their addition among themselves. The operation of adding points. This information and their understanding are necessary for an accessible presentation of the factorization algorithm for natural (integer) numbers, which has long been known to cryptology specialists by H. Lenstra's publications from 1987 and later improvements by R. Montgomery 1992 [2, 4, 5, 6, 7, ten ]. To define an elliptic curve E a, b (F p ) over a field, at first, the field is defined by the characteristic of a finite field — a prime number N or p> 3. To set the coefficients a and b of an elliptic curve E (a, b) defined over a finite simple field Fp, one can use the approach from the national standard. ( GOST ).
Thus, the elliptic curve E a, b (F p ) is the set {(x, y)} of pairs of numbers , elements of the field x, y ∊ Fp satisfying the relation y 2 ≡ x 3 + ax + b (modp), where a , b∊Fr. In E a, b (F p ) the discriminant is -4 3 + 27b 2 ≢ 0 (modp) and is not comparable with zero modulo p. It is more correct to say this is the group of points of EC, and not the curve itself. But such a replacement of concepts in something simplifies the presentation.
The EC coefficients a and b are determined by the relations a ≡ 3k (modp); b 3k (modp);
where k ≡ J (E) (1728 - J (E)) -1 (modp); J (E) ≡ 1728 ∙ 4a 3 (4a 3 + 27b 2 ) -1 (modp) EC invariant; J (E) ∨ 0∨1728.
Pairs of numbers (x, y) that satisfy the EC equation are called its points, denoted by Q (x, y), and x and y are the coordinates of the point. As a neutral element, a group of EC points includes a special point (O), a point remote to infinity (∞), its coordinates are usually not calculated. The operation of addition (+) is introduced on the set of all integer points of EC. For two arbitrary points Q 1 (x 1 , y 1 ) and Q 2 (x 2 , y 2 ) of the curve E (a, b), the summation is performed using different formulas depending on the coordinate relation of the points.
If both coordinates are equal, the points x 1 = x 2 , y 1 = y 2 ≠ 0, we have a doubling or the sum of one point with itself. The resulting point Q 3 (x 3 , y 3 ) gets the coordinates calculated by the formulas
x 3 ≡ λ 2 - 2x 1 (modp);
y 3 ≡ λ (x 1 - x 3 ) - y 1 (modp),
where λ ≡ (3x 1 2 + a) (2 1 ) -1 (modp).
At x 1 ≠ x 2 the sum of the points Q 1 (x 1 , y 1 ) and Q 2 (x 2 , y 2 ) is the point Q 3 (x 3 , y 3 ), which receives the coordinates calculated by the formulas
x 3 ≡ λ 2 - x 1 - x 2 (modp);
y 3 ≡ λ (x 1 -x 3 ) - y 1 (modp),
where λ ≡ (y 2 - y 1 ) (x 2 - x 1 ) -1 (modp).
For x 1 = x 2 , y 2 = - y 1 (modp), the points lie on the vertical line intersecting the EC in them. This straight line intersects the third point (O) EC, which is removed at infinity. The sum of the points Q 1 (x 1 , y 1 ) and Q 2 (x 2 , y 2 ) is called the neutral element (zero point O) of the group, whose coordinates are not determined. Summation with this point of any other point does not change this other and gives the result Q + O = O + Q = Q.
The point Q has the multiplicity k or is simply called the multiple point E (a, b) if for some point P∊E (a, b) the equality Q = P + P + ... + P = kP holds. If for point it is true + + ... + = kP = , then k is the order of point R.
The operation of summation of all integer points E (a, b) together with the zero point O (neutral element) generates a finite (commutative) additive (Abelian) group of order q, where q ≠ p. For this order, the Has + relation established by p + 1 - 2√r <q <p + 1 + 2√r is valid.
A SIMPLE CRYPTOGRAPHIC SYSTEM ON ELLIPTIC CURVES
In the data exchange network for all subscribers, the total reduced elliptic curve E a, b (F p ) over the field F p and the generating point P = (x, y) on it are set. Each subscriber, using the points of the additive group of this EC, forms its public and private keys. Below in example 2, a simple version of a cryptographic system (CGS) with the ability to encrypt / decrypt messages with elements of a group of points of EC is considered. Understanding the basics of the theory of elliptic curves and related issues opens up the possibility of using a rich arsenal of their tools in order to increase the level of information systems security and prevent possible attacks on them.
The basic rules of the protocol. The sender encrypts his message with the recipient's public key, the recipient uses the private key to decrypt the received encrypted messages. The public keys of all subscribers are accessible to all, the private (private) keys are kept secret from all.
Encryption : Let the sender B send to the recipient A a message in the form of a source text (IT) of one three-letter word “DOM”
These characters must be converted into a digital (binary) form, for example, an ASCII code.
IT = {IT1 = D = E4 = 1110 1000, IT2 = O = EE = 1110 1110, IT3 = M = EC = 1110 1100}
To character-encrypt a message to subscriber B, subscriber A's public key is required. Subscriber A generates this key and publishes it as publicly available on the communications network.
Public key A: point generator group EK Q = P5 = (3.3). The choice of this point is quite arbitrary. Further, A generates a random number a = 3 which for subscriber A is a private (sometimes called a secret key) key. Point Q is multiplied by the private key. It turns out the point N = aQ = 3Q = 3P5 = P11 = (6,3). the final public key is: Q, N.
The sender B generates his random number b = 2 and multiplies both points of the public key Q and N by b = 2: gets the points R = bQ = P4 = (2,5); S = bN = baQ = P8 = (4, 5).
Then the coordinates of the point S = (4, 5) are converted to the binary representation S = P8 = (4, 5) = (0000 0100, 0000 0101). The characters of the message and the xs coordinate are then converted into cipher text (PC). The simplest way to convert message text with EXOR operation
= {1 = 1110 1100; 2 = 1110 1010; 3 = 1110 1000}.
Sender B sends to recipient A a point EK R and an encrypted message.
Decryption : performs side A - the recipient of the message. The point R of the curve is multiplied by the personal (secret) key (a) of subscriber A: aR = abQ = S = 3P4 = P8 = (4,5), which also gives the point S = P8 = (4,5). Subscriber A then performs decryption, obtaining the source text of the IT.
Here is a very simplified version of encrypted messaging, when both subscribers use the same shared key. In fact, each symbol of the source text can be represented by an EC point or a coordinate of such a point. In the latter case, a group operation is used to convert the points of EC modulo.
Example 2


k is the number of terms equal to the point Pi of the corresponding line. The cells of tables 4 and 5 contain the numbers i of points of Pi from table 3, where all 13 points of the final additive group of an elliptic curve y 2 ≡ x 3 + 3 (mod7) are presented
ALGORITHM OF NUMBER OF FACTORIZATION
This probabilistic algorithm displays the main features of its presentation in [3, 7, 9].
1 Choose the number N and the number 1 <a, x, y <N;
2 we assume b = y 2 - x 3 - ah (modN). Then for EC y 2 ≡ x 3 + ah + b (moN), where a, b, x, y ∊ Fp choose the point P = (x, y);
3 Find d = NOD (N, 4 3 + 27b 2 ), if 1 <d <N, then d | N and the problem is solved, if d = 1, then go to the next step;
4 Choose the number k = LCM (2, 3, ..., M), M is a natural number;
5 Calculate multiple points kP on EC, k = 2,3, ..;
6 Calculate d = NOD (N, x k - x k-1 ),
if 1 <d <N, then d | N problem solved, divider N found,
if d = 1, then either go to step 4 and increase k, or go back to step 1 and select the parameters of the new curve,
if d = 1, then go to step 4 and decrease k.
For factorization, a compound odd number n is specified. An integer k is chosen equal to the product of the degrees of small primes with bounded exponents:
k = 2 d2 3 d3 5 d5 ... r dr . Here 2, 3, 5, ..., r are some of the first prime numbers, and d2, d3, d5, ... dr are small positive numbers. After that, a k - 1 is calculated modulo n and then (n, and k - 1), which requires 2 ℓog 2 (2kn) operations to be calculated. k n .
(n, k — 1) ≠ n, n. n , , . (n, k -1) = n, . (n, k — 1) = 1, k . [3] :
((2 +(1))ℓogpℓogℓogp) 1/2 ℓog 2 N , — N.
A specific numerical example of a factorization of a number is given below with explanations of individual computational elements.
Example 3 . This example shows the possibility of solving the problem of number factorization (the composite module of a numerical residue ring) using EC. The algorithm is based on the multiple summation of the EC point with itself, i.e. calculating the additive order of the EC point. This order divides the order of the group of points of the EC. In this case, it is possible that the solution of the factorization problem appears earlier than the order of the point is found in the process of calculating multiple points. Finding the sum of two points requires calculating the coefficient λ, for which the extended GCD (N, x 2 - x 1 ) Euclidean algorithm is involved .
d = >1, d ≠ N, N . N = 455839= 599•761. : 2 ≡ 3 + 5 -5(modN), = b = 5∊ ZN (, b) -4 3 + 27b 2≢ 0 (modN) is not comparable to zero modulo N. A rational point P = (1,1) on the EC is also given. We will repeatedly summarize this point with us. Sooner or later, such summation will lead to a result — a neutral element — a point (0), since each element of the algebraic structure has a period. Of course, this summation is a very lengthy process, but the algorithm, it turns out, can often lead to a solution at the intermediate step of the calculations. Therefore, for large numbers, we will first find a small sum of points, for example, 10! = 2 8 • 3 4 • 5 2 • 7 = 3628800 • and with their deficiency increase the number.
Let's start with a double point P 2 = 2! = 1 • 2 • . Find for P 2 the value of λ≡ (3x 1 2 + )(2 1 ) -1 (modN) = (3•1 2 + 5)/(2•1)≡4(modN) 2
2 ≡ λ 2 — 2 1 (modN) = 4 2 — 2•1(modN) = 14;
2 ≡ λ( 1 — 2 ) — 1 (modN) = 4(1 — 14) — 1(modN) = -53(modN) => -53(modN) = 455839-53 = 455786.
2 , 2 ≠ 0, 2 , . , 2 = ( 2 , 2 ) .
2 2 = (-53) 2 = 2809 = 14 3 + 5•14 — 5 = 2744+70 — 5 = 2809(modN), 2 ∊ .
3 = 3! = 1•2•3•=6 =2+ 4. 2 2 = 4, 2 . 2 2
λ ≡ (3 2 2 + )(2 2 ) -1 (modN) = (3•196 + 5)/(2(-53)) = — 593/106 = 322522(modN)
2 2
2 ≡ λ 2 — 2 1 (modN) = 259851;
2 ≡ λ( 1 — 2 ) — 1 (modN) = 116255(modN).
In calculating the coefficient λ = 322522, arithmetic of the field, ring, and EC is used. The fact is that in algebraic structures there is no division operation by number. When it appears in formulas, it must be eliminated, which is done by multiplying by the inverse element that stands in the denominator of the formula. The definition of such an inverse element is possible if the element is reversible (in the finite residue ring, not all elements have inverses). For the expression λ = - 593/106 (mod455839) we have just such a case, i.e. for element 106, it is necessary to determine the element inverse to it in the finite ring modulo N. We will show how this can be done in our example; an extended search algorithm is used to find the greatest common divisor of two numbers: the module 455839 and the denominator λ of the number 106:
455839 = 4300 • 106 + 39;
106 = 2 • 39 + 28;
39 = 1•28 + 11;
28 = 2•11 + 6;
11 = 1•6 + 5;
6 = 1•5 + 1. , (455839, 106) = 1. 106;
1= 6 — 5 = 2•6 — 11 = 2•28 — 5•11 = 7•28 — 5•39 = 81707•106 — 19•455839 => 81707•106 — 19•455839 ≡ 1(mod455839) =>81707•106 ≡ 1(mod455839) , , 1/106 ≡ 81707(mod455839).
λ = — 593/106(mod455839) => λ = — 593•81707(mod455839) = 322522.
3 2 4. λ
3 ≡ λ 2 - 1 — 2 (modN) = 195045;
3 ≡ λ( 1 — 3 ) — 2 (modN) = 123227(modN).
4 = 4! , 5 = 5! … 8 = 8! , λ 599, d= (455839, 599) d = 599, .. N, . N/599 = 761. .
List of used sources
[1] Ayerlend K., Rozen M. A classic introduction to modern number theory. - M .: Mir, 1987. -416s.
[2] Bolotov A.A. et al. An elementary introduction to elliptic cryptography. Algebras. and algorithmic principles.-M .: KomKniga, 2006.-328 p.
[3] Vasilenko O.N. Number-theoretic algorithms in cryptography. - M .: MTSNMO, 2003.-328 p.
[4] Zhdanov ON, Chalkin V.A. Elliptic curves. Fundamentals of the theory and cryptographic applications. -M .: KN. House "LIBROKOM", 2012.-200s.
[5] Ishmukhametov S.T. Factorization methods for natural numbers .- Kazan: Kazan.un-t, 2001.-190 p. (Http://www.ksu.ru/f9/bibl/Monograph_ishm,pdf)
[6] E. Knapp. Elliptic curves .- M .: Factorial-press, 2004.-488 p.
[7] Koblitz NA Course in Namber theory and cryptography. Springer-Verlag, 1987.
[8] Lenstra HW (1987) Factoring integer with elliptic curves. Ann.of Math.126(2),649-673.(http://www.ams.org/mathscinet-getitem?mr=89g:11125).
[9] .. . .--: - - .,2003.-192.
[10] .. .- .: , 1991. — 368 .
Source: https://habr.com/ru/post/247179/
All Articles