About the diagonal of the square
The introduction of complex numbers into circulation was by no means the first revolution in human understanding of the nature of numbers. Two thousand years before this powerful shock, the world of ancient Greek mathematics experienced.
The troubles of the Pythagoreans did not begin immediately. The scientific school founded by Pythagoras ended badly in the end, but today's story is not about the vigorous pogrom that was perpetrated over the Pythagoreans by the thankful people for their enlightenment, but to a greater degree about the spiritual upheavals.
The term "scientific school" in relation to an organization founded by Pythagoras is a kind of euphemism. Sensibly looking at its structure and applied technologies, Pythagoreanism should be boldly attributed to totalitarian cults, which was quite in the spirit of the times (however, it is always in the spirit of the times, an eternal classic). There was a division into degrees of initiation, and a complex system of rituals with prohibitions (for example, well-known, such as “not eating beans” or “not biting off a whole roll”), and complex philosophical dogma. Hello Ron Hubbard associates. There is nothing new under the sun.
')
In general, during the life of Pythagoras, his "school" was a solid enterprise, besides having significant and growing political influence.
In general, the philosophy of Pythagoras had a significant impact on Western culture (and for us as well). Many ideas have been developed in classical Greek philosophy, and already everyone knows about the Pythagorean theorem. The expression "harmony of the spheres", by the way, also goes back to the Pythagoreans.
One of the essential elements of their philosophy was the idea that any number can be represented as the ratio of two integers, that is, in the form of a simple fraction. In this they, among other things, saw the perfection of the nature of the number. Moreover, it seemed quite obvious. In modern mathematics, such numbers are called rational, and their set is denoted by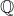 . Now pause for a few seconds, think about where it all comes from, what's wrong? Can you give an argument that would be convincing enough for an ancient Greek? Well, or at least convincing enough for yourself, personally?
. Now pause for a few seconds, think about where it all comes from, what's wrong? Can you give an argument that would be convincing enough for an ancient Greek? Well, or at least convincing enough for yourself, personally?
In general, the world of numbers was simple, elegant, and everyone was happy. The source of the trouble, unexpectedly, was the already mentioned theorem bearing the name of Pythagoras: one of the most important achievements of ours. Unfortunately, the proof of Pythagoras himself is unknown to us. The oldest of those that have come down to us is given in the Euclidean Principles and dates back to the 3rd c. dn Let me remind you, Pythagoras himself lived in the 6th c. dn
Fragment from Vatican Manuscript Number 190, dated 10th c. ne (whole here ):

The proof of Euclid is far from the simplest. There is reason to believe that he knew the way and simpler, but for methodical reasons he brought this option, which, in addition to the Pythagorean theorem itself, demonstrates some other interesting ideas.
However, back to the Pythagoreans.
Imagine the simplest thing: a square with sides of unit length. If we denote the length of its diagonal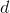 then by the Pythagorean theorem we get:
then by the Pythagorean theorem we get:

and correspondingly:

By itself, this is not a problem. From the point of view of the Pythagoreans, then you just had to find the integers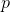 and
and 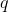 such that
such that
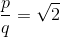
It was on this “simple” moment that everything stalled. And tightly. This stopper lasted until one clever man (as they say, Hippas from Metapont, also a Pythagorean), proved, suddenly, that there are no such numbers. All the evil from the very smart goes, as you know. According to legend, this scientific achievement so shocked colleagues that, to mark the recognition of scientific merit, Hippas was not promptly thrown overboard the ship, on which he sailed at the time of his mathematical insight. But there was nothing to spoil respected people, to undermine the foundations of such a lovingly fostered and highly profitable philosophical system.
Now, the numbers are not representable as the ratio of two integers, called irrational.
For some time, the Pythagoreans even kept the fact of irrationality in secret. However, you cannot conceal the sewing in a bag, and the truth rather quickly (by historical standards) found its way out.
in secret. However, you cannot conceal the sewing in a bag, and the truth rather quickly (by historical standards) found its way out.
Prove irrationality not at all difficult.
not at all difficult.
Let there be such , what
, what
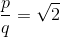
Moreover, we assume that at least one of the numbers - odd. If this is not the case, the numerator and denominator of the fraction can always be reduced by 2 (the required number of times).
- odd. If this is not the case, the numerator and denominator of the fraction can always be reduced by 2 (the required number of times).
Then we get:
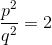
from here:

In this way, - even number. But then
- even number. But then 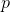 - even.
- even.
By the condition of oddness of at least one of the numbers , we get that
, we get that 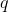 - odd.
- odd.
By parity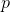 you can write
you can write
 ,
,
Where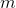 - some whole.
- some whole.
But then:

from here

But it means that - even, which means even
- even, which means even 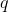 . Contradiction.
. Contradiction.
Number cannot be represented as a ratio of two integers.
cannot be represented as a ratio of two integers.
It remains to add that - this is not at all some strange freak. It can be shown that there are more irrational numbers than rational ones, basically more. By the way, the more-less relationship in the world of infinite sets is itself very controversial. But that's another story.
- this is not at all some strange freak. It can be shown that there are more irrational numbers than rational ones, basically more. By the way, the more-less relationship in the world of infinite sets is itself very controversial. But that's another story.
Ps. Taking this opportunity, I congratulate the habrovchan on coming. Good luck in the new year!
UPD. In connection with the discussion that has flared up in the comments, I would like to note the following: to be honest, rational numbers are entered as a field of partial rings of integers. Whether to use as a multiplicative system many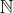 or many
or many 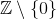 - purely a matter of taste, does not affect the result. The question of which of the school pseudo-definitions is “true” is decided by the Ministry of Education, and this process has very little to do with mathematics.
- purely a matter of taste, does not affect the result. The question of which of the school pseudo-definitions is “true” is decided by the Ministry of Education, and this process has very little to do with mathematics.
The troubles of the Pythagoreans did not begin immediately. The scientific school founded by Pythagoras ended badly in the end, but today's story is not about the vigorous pogrom that was perpetrated over the Pythagoreans by the thankful people for their enlightenment, but to a greater degree about the spiritual upheavals.
The term "scientific school" in relation to an organization founded by Pythagoras is a kind of euphemism. Sensibly looking at its structure and applied technologies, Pythagoreanism should be boldly attributed to totalitarian cults, which was quite in the spirit of the times (however, it is always in the spirit of the times, an eternal classic). There was a division into degrees of initiation, and a complex system of rituals with prohibitions (for example, well-known, such as “not eating beans” or “not biting off a whole roll”), and complex philosophical dogma. Hello Ron Hubbard associates. There is nothing new under the sun.
')
In general, during the life of Pythagoras, his "school" was a solid enterprise, besides having significant and growing political influence.
In general, the philosophy of Pythagoras had a significant impact on Western culture (and for us as well). Many ideas have been developed in classical Greek philosophy, and already everyone knows about the Pythagorean theorem. The expression "harmony of the spheres", by the way, also goes back to the Pythagoreans.
One of the essential elements of their philosophy was the idea that any number can be represented as the ratio of two integers, that is, in the form of a simple fraction. In this they, among other things, saw the perfection of the nature of the number. Moreover, it seemed quite obvious. In modern mathematics, such numbers are called rational, and their set is denoted by
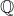 . Now pause for a few seconds, think about where it all comes from, what's wrong? Can you give an argument that would be convincing enough for an ancient Greek? Well, or at least convincing enough for yourself, personally?
. Now pause for a few seconds, think about where it all comes from, what's wrong? Can you give an argument that would be convincing enough for an ancient Greek? Well, or at least convincing enough for yourself, personally?In general, the world of numbers was simple, elegant, and everyone was happy. The source of the trouble, unexpectedly, was the already mentioned theorem bearing the name of Pythagoras: one of the most important achievements of ours. Unfortunately, the proof of Pythagoras himself is unknown to us. The oldest of those that have come down to us is given in the Euclidean Principles and dates back to the 3rd c. dn Let me remind you, Pythagoras himself lived in the 6th c. dn
Fragment from Vatican Manuscript Number 190, dated 10th c. ne (whole here ):

The proof of Euclid is far from the simplest. There is reason to believe that he knew the way and simpler, but for methodical reasons he brought this option, which, in addition to the Pythagorean theorem itself, demonstrates some other interesting ideas.
However, back to the Pythagoreans.
Imagine the simplest thing: a square with sides of unit length. If we denote the length of its diagonal
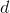 then by the Pythagorean theorem we get:
then by the Pythagorean theorem we get:
and correspondingly:

By itself, this is not a problem. From the point of view of the Pythagoreans, then you just had to find the integers
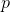 and
and 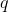 such that
such that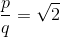
It was on this “simple” moment that everything stalled. And tightly. This stopper lasted until one clever man (as they say, Hippas from Metapont, also a Pythagorean), proved, suddenly, that there are no such numbers. All the evil from the very smart goes, as you know. According to legend, this scientific achievement so shocked colleagues that, to mark the recognition of scientific merit, Hippas was not promptly thrown overboard the ship, on which he sailed at the time of his mathematical insight. But there was nothing to spoil respected people, to undermine the foundations of such a lovingly fostered and highly profitable philosophical system.
Now, the numbers are not representable as the ratio of two integers, called irrational.
For some time, the Pythagoreans even kept the fact of irrationality
Prove irrationality
Let there be such
 , what
, what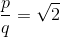
Moreover, we assume that at least one of the numbers
 - odd. If this is not the case, the numerator and denominator of the fraction can always be reduced by 2 (the required number of times).
- odd. If this is not the case, the numerator and denominator of the fraction can always be reduced by 2 (the required number of times).Then we get:
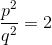
from here:

In this way,
 - even number. But then
- even number. But then 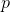 - even.
- even.By the condition of oddness of at least one of the numbers
 , we get that
, we get that 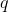 - odd.
- odd.By parity
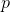 you can write
you can write ,
,Where
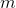 - some whole.
- some whole.But then:

from here

But it means that
 - even, which means even
- even, which means even 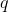 . Contradiction.
. Contradiction.Number
It remains to add that
Ps. Taking this opportunity, I congratulate the habrovchan on coming. Good luck in the new year!
UPD. In connection with the discussion that has flared up in the comments, I would like to note the following: to be honest, rational numbers are entered as a field of partial rings of integers. Whether to use as a multiplicative system many
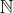 or many
or many 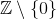 - purely a matter of taste, does not affect the result. The question of which of the school pseudo-definitions is “true” is decided by the Ministry of Education, and this process has very little to do with mathematics.
- purely a matter of taste, does not affect the result. The question of which of the school pseudo-definitions is “true” is decided by the Ministry of Education, and this process has very little to do with mathematics.Source: https://habr.com/ru/post/246963/
All Articles