Whence there is a complex number
In modern mathematics, a complex number is one of the most fundamental concepts, which is applied both in “pure science” and in applied fields. It is clear that this was not always the case. In the distant past, when even the usual negative numbers seemed a strange and dubious innovation, the need to expand the square root operation on them was not at all obvious. Nevertheless, in the middle of the XVI century, the mathematician Raphael Bombelli introduces complex (in this case more precisely, imaginary) numbers into circulation. Actually, I propose to look at what was the essence of the difficulties, which resulted in a solid Italian at the end of such extremes.
There is a common misconception that complex numbers are required in order to solve quadratic equations. Actually, this is absolutely not the case: the problem of finding the roots of a quadratic equation does not in any way motivate the introduction of complex numbers. That's perfect.
Let's see for yourself. Any quadratic equation can be represented as:
 .
.
Geometrically, this means that we want to find the crossing points of some straight line and parabolas
and parabolas 
I even made a picture here, for illustration.

As we all know well from school, the roots of the quadratic equation (in the above notation) are found using the following formula:

')
There are 3 possible options:
1. The radical expression is positive.
2. The radical expression is zero.
3. The radical expression is negative.
In the first case, there are 2 different roots, in the second two are the same, in the third, the equation is “not solved”. All these cases have quite a clear geometric interpretation:
1. A straight line intersects a parabola (the blue straight line in the figure).
2. The straight line concerns the parabola.
3. A straight line does not have common points with a parabola (the lilac straight line in the figure).
The situation is simple, logical, consistent. There is absolutely no reason to try to extract the square root from a negative number. No one tried.
The situation changed significantly when an inquiring mathematical thought reached the cubic equations. Slightly less obvious, using some simple substitution , every cubic equation can be reduced to the form: . From a geometrical point of view, the situation is similar to the previous one: we are looking for the intersection point of a straight line and a cubic parabola.
. From a geometrical point of view, the situation is similar to the previous one: we are looking for the intersection point of a straight line and a cubic parabola.
Take a look at the picture:

The essential difference from the case of a quadratic equation is that no matter which straight line we take, it always crosses a parabola. That is, from purely geometric considerations, a cubic equation always has at least one solution.
You can find it using the Cardano formula:
![x = \ sqrt [3] {\ frac {b} {2} + \ sqrt {\ Phi}} + \ sqrt [3] {\ frac {b} {2} - \ sqrt {\ Phi}},](https://habrastorage.org/getpro/habr/post_images/b9e/3f1/478/b9e3f14783ad0b2458bdc73bb5b35609.png)
Where
 .
.
A bit cumbersome, but so far, it seems, everything is in order. Or not?
In general, the Cardano formula is a vivid example of the “Arnold principle” in action. And characteristically, Cardano never claimed to have authorship of a formula.
Let us return, however, to our sheep. The formula is wonderful, without exaggeration, the great achievement of mathematics in the early to mid-sixteenth century. But she has one nuance.
Take the classic example that was considered by Bombelli:
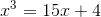 .
.
Suddenly,
 ,
,
and correspondingly,
![x = \ sqrt [3] {2+ \ sqrt {-121}} + \ sqrt [3] {2- \ sqrt {-121}}.](https://habrastorage.org/getpro/habr/post_images/d75/006/448/d7500644862f9b71205db936e51cbf4a.png) .
.
Sailed. And the formula is a pity, but the formula is good. Dead end. Given that the equation, of course, has a solution.
The idea of Rafael Bombelli was as follows: let's pretend to be a hose and pretend that the root of the negative is a certain number. Of course, we know that there are no such numbers, but nevertheless, let us imagine that it exists and, like ordinary numbers, it can be added to others, multiplied, raised to a power, etc.
Using a similar approach, Bombelli established, in particular, that
![\ sqrt [3] {2+ \ sqrt {-121}} = 2 + \ sqrt {-1}](https://habrastorage.org/getpro/habr/post_images/f00/489/9f8/f004899f88be98b309119149c8b10cc9.png) ,
,
and
![\ sqrt [3] {2- \ sqrt {-121}} = 2 - \ sqrt {-1}.](https://habrastorage.org/getpro/habr/post_images/409/98a/96c/40998a96c1da44e529e5a9c0d8252d06.png) .
.
Let's check:
 .
.
Notice, in the calculations, no assumptions about the properties of the square roots of negative numbers were assumed, except for the above assumption that they behave like "ordinary" numbers.
In total, we get . That is quite a correct answer, which is elementary verified by direct substitution. It was a real breakthrough. Breakthrough in the complex plane.
. That is quite a correct answer, which is elementary verified by direct substitution. It was a real breakthrough. Breakthrough in the complex plane.
Nevertheless, such calculations look like some magic, a mathematical focus. The attitude towards them, as to a certain trick, remained among mathematicians for a very long time. Actually, invented by Rene Descartes for the roots of the negative name "imaginary numbers" fully reflects the attitude of mathematicians of those times to such entertainment.
However, as time went on, the “trick” was applied with unchanged success, the authority of “imaginary numbers” in the eyes of the mathematical society grew, restrained, however, by the inconvenience of their use. Only getting Leonard Euler (by the way, it was he who introduced the now commonly used designation for imaginary unit) famous formula
for imaginary unit) famous formula

opened the way for complex numbers to the most diverse areas of mathematics and its applications. But that's another story.
There is a common misconception that complex numbers are required in order to solve quadratic equations. Actually, this is absolutely not the case: the problem of finding the roots of a quadratic equation does not in any way motivate the introduction of complex numbers. That's perfect.
Let's see for yourself. Any quadratic equation can be represented as:
 .
.Geometrically, this means that we want to find the crossing points of some straight line
 and parabolas
and parabolas 
I even made a picture here, for illustration.

As we all know well from school, the roots of the quadratic equation (in the above notation) are found using the following formula:

')
There are 3 possible options:
1. The radical expression is positive.
2. The radical expression is zero.
3. The radical expression is negative.
In the first case, there are 2 different roots, in the second two are the same, in the third, the equation is “not solved”. All these cases have quite a clear geometric interpretation:
1. A straight line intersects a parabola (the blue straight line in the figure).
2. The straight line concerns the parabola.
3. A straight line does not have common points with a parabola (the lilac straight line in the figure).
The situation is simple, logical, consistent. There is absolutely no reason to try to extract the square root from a negative number. No one tried.
The situation changed significantly when an inquiring mathematical thought reached the cubic equations. Slightly less obvious, using some simple substitution , every cubic equation can be reduced to the form:
 . From a geometrical point of view, the situation is similar to the previous one: we are looking for the intersection point of a straight line and a cubic parabola.
. From a geometrical point of view, the situation is similar to the previous one: we are looking for the intersection point of a straight line and a cubic parabola.Take a look at the picture:

The essential difference from the case of a quadratic equation is that no matter which straight line we take, it always crosses a parabola. That is, from purely geometric considerations, a cubic equation always has at least one solution.
You can find it using the Cardano formula:
![x = \ sqrt [3] {\ frac {b} {2} + \ sqrt {\ Phi}} + \ sqrt [3] {\ frac {b} {2} - \ sqrt {\ Phi}},](https://habrastorage.org/getpro/habr/post_images/b9e/3f1/478/b9e3f14783ad0b2458bdc73bb5b35609.png)
Where
 .
.A bit cumbersome, but so far, it seems, everything is in order. Or not?
In general, the Cardano formula is a vivid example of the “Arnold principle” in action. And characteristically, Cardano never claimed to have authorship of a formula.
Let us return, however, to our sheep. The formula is wonderful, without exaggeration, the great achievement of mathematics in the early to mid-sixteenth century. But she has one nuance.
Take the classic example that was considered by Bombelli:
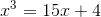 .
.Suddenly,
 ,
,and correspondingly,
![x = \ sqrt [3] {2+ \ sqrt {-121}} + \ sqrt [3] {2- \ sqrt {-121}}.](https://habrastorage.org/getpro/habr/post_images/d75/006/448/d7500644862f9b71205db936e51cbf4a.png) .
.Sailed. And the formula is a pity, but the formula is good. Dead end. Given that the equation, of course, has a solution.
The idea of Rafael Bombelli was as follows: let's pretend to be a hose and pretend that the root of the negative is a certain number. Of course, we know that there are no such numbers, but nevertheless, let us imagine that it exists and, like ordinary numbers, it can be added to others, multiplied, raised to a power, etc.
Using a similar approach, Bombelli established, in particular, that
![\ sqrt [3] {2+ \ sqrt {-121}} = 2 + \ sqrt {-1}](https://habrastorage.org/getpro/habr/post_images/f00/489/9f8/f004899f88be98b309119149c8b10cc9.png) ,
,and
![\ sqrt [3] {2- \ sqrt {-121}} = 2 - \ sqrt {-1}.](https://habrastorage.org/getpro/habr/post_images/409/98a/96c/40998a96c1da44e529e5a9c0d8252d06.png) .
.Let's check:
 .
.Notice, in the calculations, no assumptions about the properties of the square roots of negative numbers were assumed, except for the above assumption that they behave like "ordinary" numbers.
In total, we get
 . That is quite a correct answer, which is elementary verified by direct substitution. It was a real breakthrough. Breakthrough in the complex plane.
. That is quite a correct answer, which is elementary verified by direct substitution. It was a real breakthrough. Breakthrough in the complex plane.Nevertheless, such calculations look like some magic, a mathematical focus. The attitude towards them, as to a certain trick, remained among mathematicians for a very long time. Actually, invented by Rene Descartes for the roots of the negative name "imaginary numbers" fully reflects the attitude of mathematicians of those times to such entertainment.
However, as time went on, the “trick” was applied with unchanged success, the authority of “imaginary numbers” in the eyes of the mathematical society grew, restrained, however, by the inconvenience of their use. Only getting Leonard Euler (by the way, it was he who introduced the now commonly used designation
 for imaginary unit) famous formula
for imaginary unit) famous formula
opened the way for complex numbers to the most diverse areas of mathematics and its applications. But that's another story.
Source: https://habr.com/ru/post/246747/
All Articles