Search for the longest word chains in Russian using the Wolfram Language (Mathematica)

Download the translation in the form of a Mathematica document that contains all the code used in the article here (archive, ~ 5 MB).
Introduction
In Russian, as in many other languages, there are words that have the same length, but differ by only one letter. These kind of word pairs are called metagrams .
Suppose we have several consecutive metagrams, say:
')
opinion-smoldering-smoldering-friction-debating-poeni-roenie-rdenie-vigil-beating
they form a chain of metagrams, or a chain of words.
Hence the game called word ladder , which was invented by Lewis Carroll back in 1879.
It is clear that not such a chain can be made up for every initial word, and some words, apparently, must generate rather long chains.
In this post we will try to analyze the chains of words that can be built in Russian, and also find the chains of the greatest length.
Import word list of Russian language
To build and analyze word strings, we need a list of words that we can meet in Russian. In this post, we will not make a restriction on the part of speech that can be used, but at the same time we will consider only the form of the word corresponding to the nominative case in the word paradigm . We use, as in one of the previous posts ( Search for the best sequence of viewing the list of 250 best films using the Wolfram Language (Mathematica) language), the morphological dictionary of the Russian language, created by Academician Andrei Anatolyevich Zaliznyak :
In [1]: =
In [3]: =

We will process the dictionary data, making on its basis a list of words of the Russian language RussianWords :
In [4]: =

The function that defines the link of the chain of words
Create a chainLinkQ function that will determine if two words can be a link in a chain of words, in other words, this function answers the question whether two words are a metagram.
In this case, we consider two options:
- words differ by one letter (in this case, it suffices to use for checking the EditDistance function, which calculates the Levenshtein distance , the result of which must be equal to 1):
In [5]: =
- words are distinguished by n adjacent letters:
In [6]: =

The search function of all metagrams of words of fixed length
Now we find all the links in the chains of words (metagrams).
To begin with, we will break all the words of the Russian language into equivalence classes , i.e., we will essentially build a factor-set of words of the Russian language by their length, in other words, we will break the list of all words into sets of words from the 1st, 2nd, 3, 4, etc. letters.
In [7]: =
Find the minimum and maximum word lengths in Russian:
In [8]: =
Out [8] =
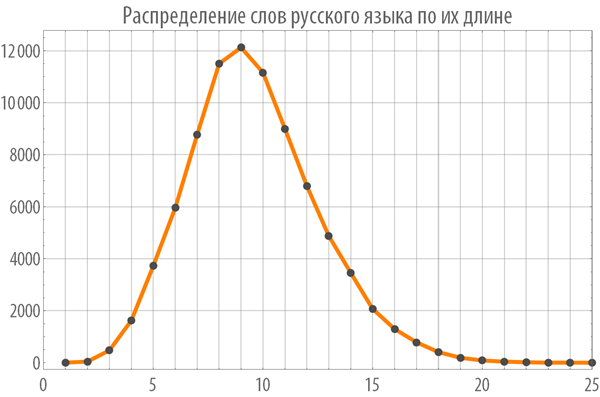
Let's look at the distribution of words of the Russian language in length:
In [9]: =

Out [9] =
Now we will create a function that preserves its calculated values, which will select among all possible word pairs of a given length those that can be links of word strings:
In [10]: =
We calculate this function for each word equivalence class of the Russian language, while we will now consider only words that differ by one letter:
In [11]: =
Example of the result of calculations:
In [12]: =
Out [12] =

Word chain graphs
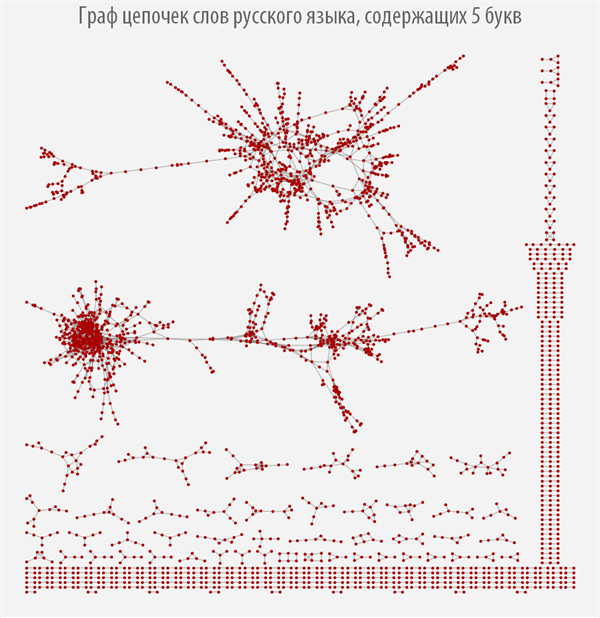
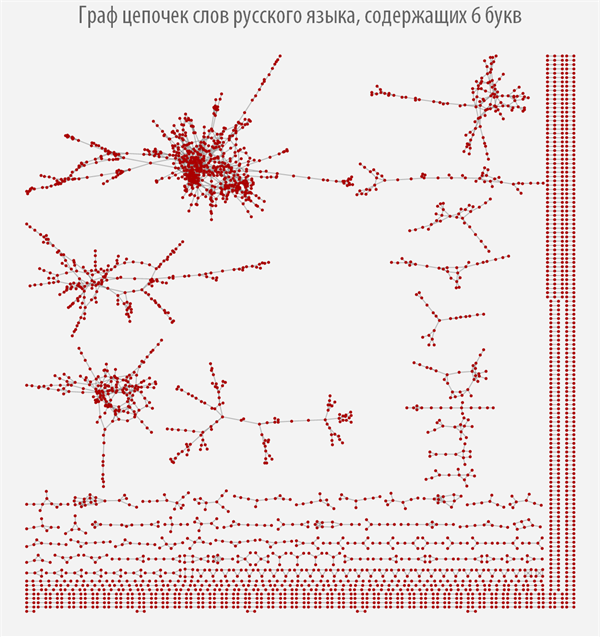
After we have computed the search function for all links in a chain of words for each equivalence class, we can construct corresponding graphs that will allow us to visually study the structure of chains of words of each type (if there is no graph, then there are no links for words of this length).
When you hover over each of the graph vertices, you can get a pop-up hint with the word that corresponds to this graph vertex (you can download the document with interactive graphs and source code from the link provided at the very beginning of the post).
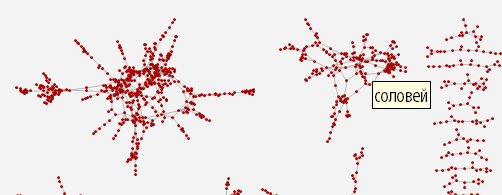
In [13]: =

In [14]: =
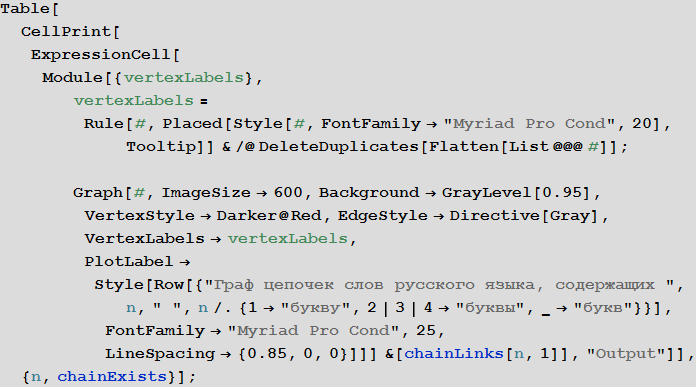
Graph of Russian word chains containing 1 letter

Graph of Russian word chains containing 2 letters

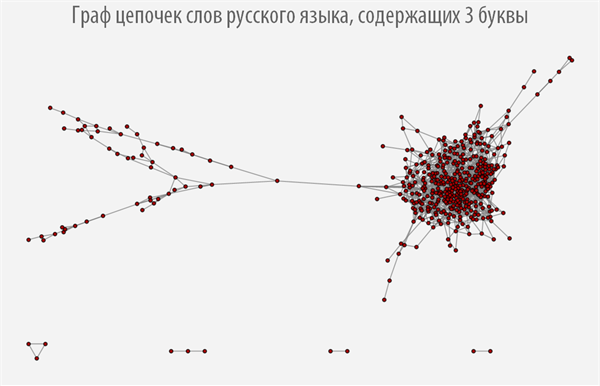
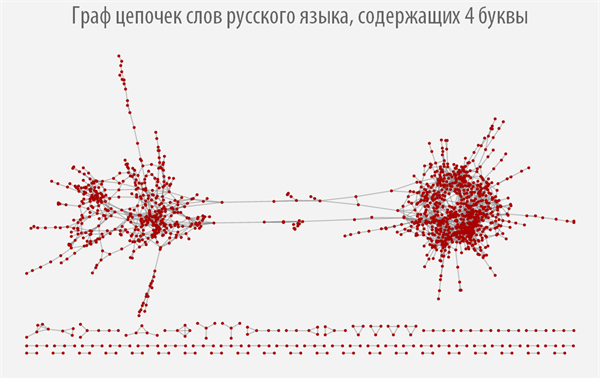

Graph of chains of words of the Russian language, containing 8 letters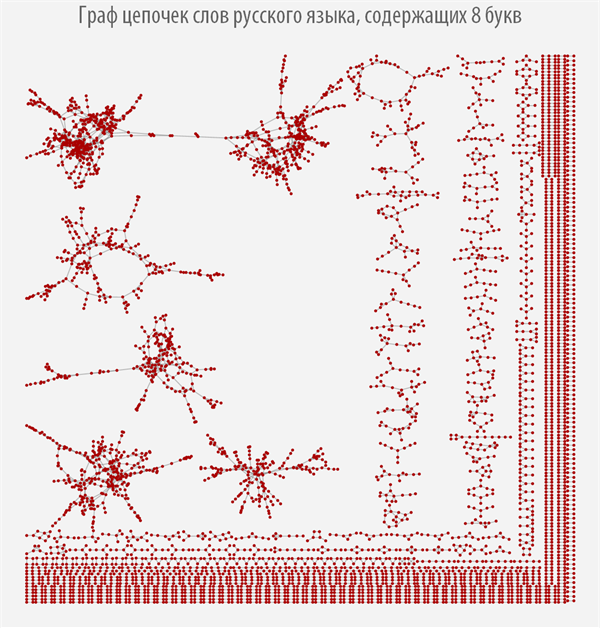

Graph of chains of words of the Russian language, containing 9 letters

Graph of chains of words of the Russian language, containing 10 letters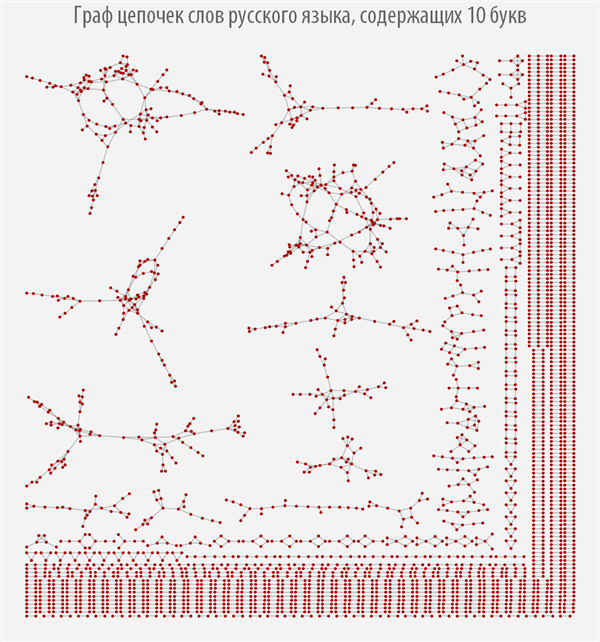

Graph of Russian word chains containing 11 letters

Graph of chains of words of the Russian language, containing 12 letters

Graph of chains of words of the Russian language, containing 13 letters

Graph of chains of words of the Russian language, containing 14 letters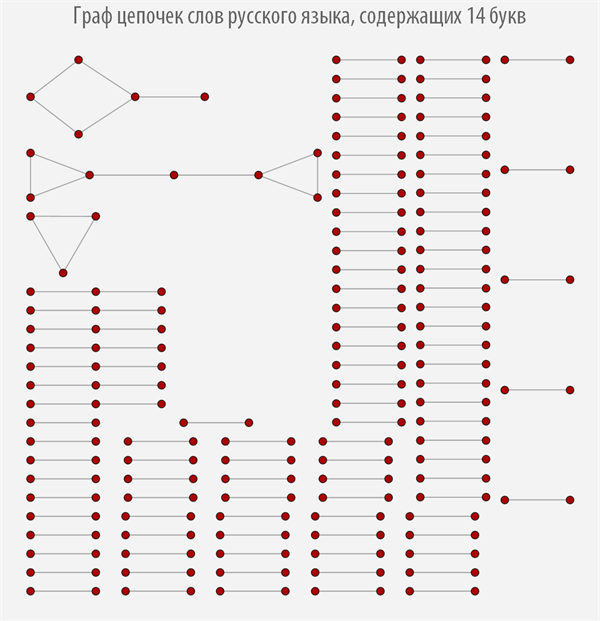

Graph of chains of words of the Russian language, containing 15 letters

Graph of chains of words of the Russian language, containing 16 letters

Graph of chains of words of the Russian language, containing 17 letters

Graph of chains of words of the Russian language, containing 18 letters

Graph of chains of words of the Russian language, containing 21 letters

It can be seen from the graphs above how strongly their structure changes depending on the length of the words from which it is built, and it can be observed that most graphs have more than one connected component.
From the graph below, we can see the dependence of the number of connected components of various lengths among all the graphs considered above, from which it follows that the dependence should have the form
In [15]: =
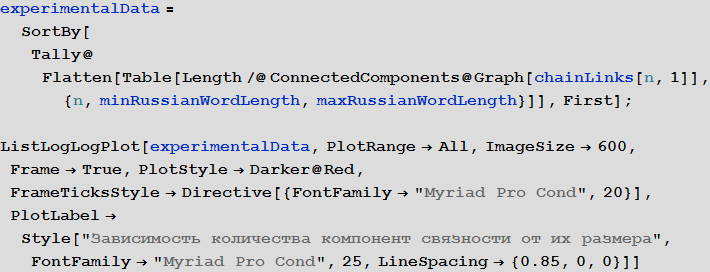
Out [16] =
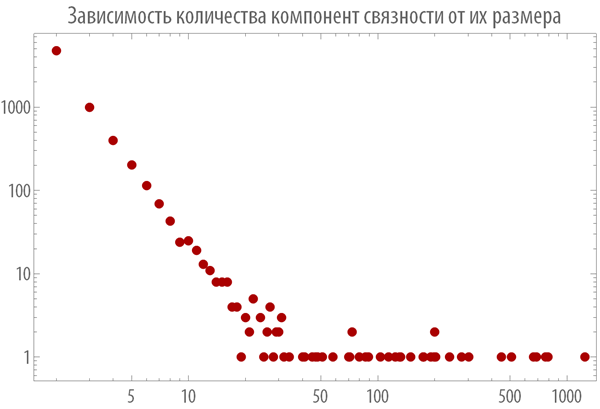
Really:
In [17]: =

Out [17] =
In [19]: =

Out [19] =
The assumption of Donald Knuth in relation to the chains of words in the Russian language
Donald Knut was one of the first to use a computer to research English language chains. He studied chains of words consisting of 5 letters, because he believed that words from a smaller number of letters, say 3, are too simple to learn (although Lewis Carroll made up a chain of 6 links from the word APE to the word MAN), and words from more letters will not be able to lead to long chains, including because the corresponding graph has many connected components.
Check Knut's assumption for the chains of words of the Russian language.
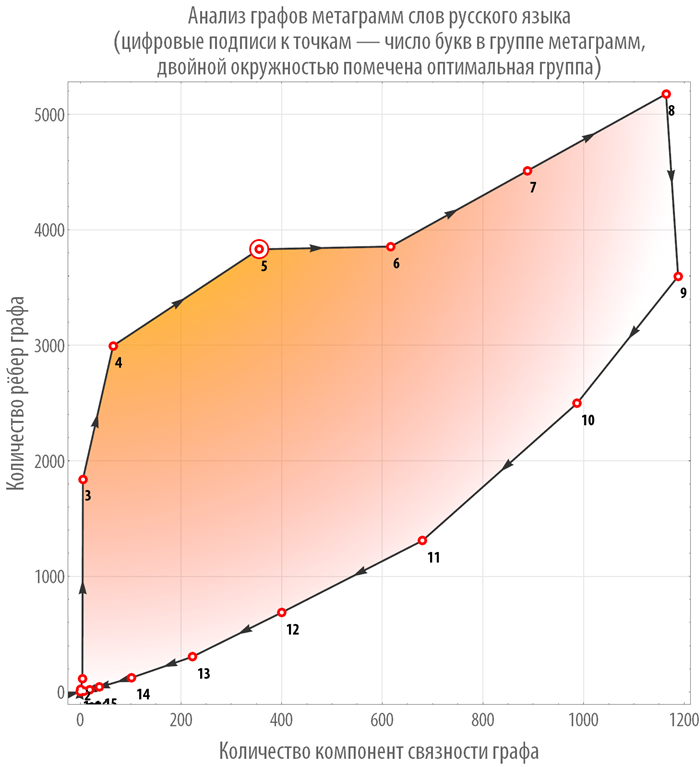
The graph below shows how with the increase in the number of letters in the words from which chains are built, the position of the point with coordinates changes:
{number of connected components of a graph, number of edges of a graph} .
The upper left corner corresponds to the “ideal graph” for which there is one connected component, with its maximum number of edges. The graph corresponding to the closest point of the trajectory under consideration to a given point can obviously be considered as “the best”. The corresponding point found automatically is marked with two red circles and corresponds to a graph of chains of five-letter words.
Thus, it can be argued that the assumption of Donald Knuth, made for chains of words of the English language, just as it is not surprising, is also true for the Russian language. Perhaps this is a fairly deep properties of human psychology, tied to the numbers 5 and 10, corresponding to the fingers on one and two palms, respectively.
In [20]: =

Out [25] =
Search for the longest string of words in Russian
So, having gone a rather long way, we are finally ready to find the longest string of words that exists in Russian. As follows from the previous section, it should be among the chains of words of five letters.
In [26]: =
Out [26] =

So, we got the two longest chains of words in Russian, while, as expected, they are contained in the “best” column of chains of five-letter words.
Search for the longest chains of n-letter words of the Russian language
In the previous section, we searched for the longest string of words in the Russian language, and we found two chains of 40 five-letter words.
Let's now look at the longest possible chains of n-letter words:
In [27]: =

Chains of words of the Russian language, containing 2 letters, with the number of words not less than 5

Chains of words of the Russian language, containing 3 letters, with the number of words not less than 5




Chains of words of the Russian language, containing 7 letters, with the number of words not less than 5

Chains of words of the Russian language, containing 8 letters, with the number of words not less than 5

Chains of words of the Russian language, containing 9 letters, with the number of words not less than 5

Chains of words of the Russian language, containing 10 letters, with the number of words not less than 5

Chains of words of the Russian language, containing 11 letters, with the number of words not less than 5

Chains of words of the Russian language, containing 12 letters, with the number of words not less than 5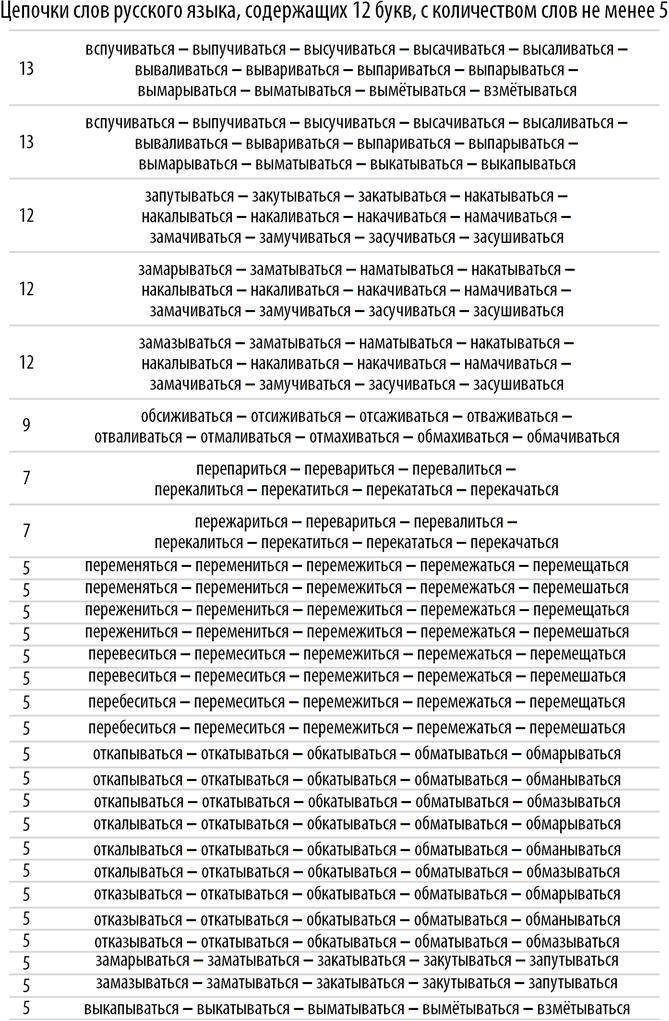

Chains of words of the Russian language, containing 13 letters, with the number of words not less than 5

Conclusion
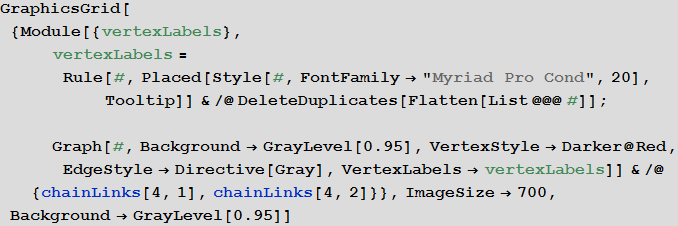
I hope that my post could interest you, and some of the ideas and programs presented in it will be useful to you. Of course, you can come up with a lot of interesting studies of the Russian language. For example, at the beginning of the post, the function chainLinkQ was created, the functionality of which allows you to perform a similar study for metagrams that differ in two letters - which corresponds, in fact, to a small modification of the rules of the game in word chains. From the two graphs presented below, it can be seen that the graph of four-letter metagrams, differing in two letters, is connected, as compared to the graph of metagrams, differing only in one letter. This suggests that the results of the study of such graphs and chains will be completely different.
In [28]: =
Out [28] =

Resources for learning Wolfram Language ( Mathematica ) in Russian: http://habrahabr.ru/post/244451
Source: https://habr.com/ru/post/246411/
All Articles