Overview of graph compression algorithms
This paper describes methods of compressing primarily social (graphs of connections between users on social networks) and Web graphs (graphs of links between sites).
Most of the algorithms on graphs are well studied and designed on the basis of the fact that random access to graph elements is possible, at the moment the size of social graphs exceed the average RAM of the average machine in size, but at the same time easily fit on the hard disk. A compromise option is to compress the data with the ability to quickly access certain queries. We will focus on two:
a) get a list of edges for a particular vertex
b) find out if 2 vertices are connected.
Modern algorithms allow compressing data up to 1-5 bits per link, which makes it possible to work with a similar database on an average machine. I was inspired to write this article precisely the desire to fit the base of vkontakte friends in 32GB of RAM, given that now there are about 300M accounts with an average peak level of about 100, it seems quite realistic. It is on this basis that I will conduct my experiments.
')
The general properties of the graphs of interest to us are:
a) the fact that they are large, 16 - 19 or more tops and about 19 edges - which makes it impossible to work with them directly in memory, but allows you to store them even on one hard drive without any problems. The site law.di.unimi.it/datasets.php presents the entire vast range of such databases.
b) the distribution of degrees (vertices) of vertices, and indeed, all important frequency characteristics are described by a power dependence (Power-Law) at least asymptotically.
c) they are sparse. The average degree of the vertex is ~ 100-1000.
d) vertices are similar - the probability that you have a common friend is more for the connected vertices.
In this paper, the graph in the "natural", uncompressed form will be represented by an array of lists:
Table 1. Natural coding of the graph. (Example taken from [2])
Let's call the difference between the indices of the two links “gap”.
The first of the families of compression algorithms are methods that use the following 2 basic approaches:
a) Exploitation of locality of vertices. Vertices more often refer to “close” peaks, rather than to “far” ones.
b) Operation of vertex similarity. “Close” vertices refer to the same vertices.
In these two statements lies a paradox - the term “proximity” of peaks can be described in the same way through similarity, then our statements will turn into a truism. It is in clarifying the concept of "proximity" that is the main difference between the algorithms I have tried.
The first work on this topic is apparently K. Randall [1]. It examined the web graph of Altavista still alive, and it was discovered that most of the links (80%) on the graph are local and have a large number of common links, and it was suggested to use the following reference coding:
- the new vertex is encoded as a link to a “similar” + list of additions and deletions, which in turn is encoded with gaps + nibble coding.
The guys squeezed the altavist to 5 bits per link (I will try to bring the worst compression results in the works). This approach has been greatly developed in the works of Paolo Boldi and Sebastiano Vigna.
They proposed a more complex method of reference coding, presented in Table 2. Each vertex can have one reference to “similar”, RefNr encodes the difference between the current vertex and it, if RefNr is zero, then the vertex has no reference. Copy list is a bit-list that encodes which vertices must be picked up by reference - if the corresponding Copy list bit is 1, then this vertex also belongs to the encoded one. Then Copylist is also encoded with RLE by a similar algorithm and turns into CopyBlocks:
We write the length - 1 for each repeating block + value of the first block (1 or 0), and the zeros remaining at the end can be discarded.
The rest of the vertices is converted into gaps, the intervals of zeros are coded separately (here a special property of web graphs is exploited, which will be discussed below) and the remaining gaps (Residuals) are recorded by one of the digitized codes ( Golomb , Huffman extremum).
As can be seen from table 2, this encoding can be multi-level - the degree of this multi-level is one of the parameters of the encoder L , with a large L, the encoding speed and decoding decreases, but the degree of compression increases.
Table 2. The method of reference coding proposed by Boldi and Vigna for data from Table 1. [2]
The distribution of Gaps in the crawler bases is also subject to Power-Law law.

Figure 1. Distribution of "Gaps" in snapshot on .uk sites - 18.5M pages.
What allowed us to say "close" accounts are given to us from above in the form of ordered data from webcrawlers. And then develop the work on the above two directions: encode the list of edges as a modification of one of the previous vertices (reference coding), store the list of edges as “Gaps” (Gap [i, 0] = Node [i] - link [i, 0]) - and, using the frequency response identified above - to encode this list with one of the many integer codes. I must say that they did well: 2-5 bit per link [4]. In [2] and [3], even simpler reference coding methods LM and SSL are proposed that encode the data in small blocks. The result is superior or rather commensurate with the BV algorithm. From myself I want to add that even a simple coding with gaps gives a comparable result on Web - bases and at the same time all methods using local "similarity" noticeably succumb to social bases.
In social graphs, this effect does not seem to be observed — in Figure 2, the distribution of gaps in different pieces of the vkontakte database is presented. It is interesting that for the first million log / log accounts, the law for gaps is actually implemented. But with the increase in the amount of data. The distribution of gaps is becoming more and more "white."
Figure 2. The distribution of gaps in the base of friends vkontakte.
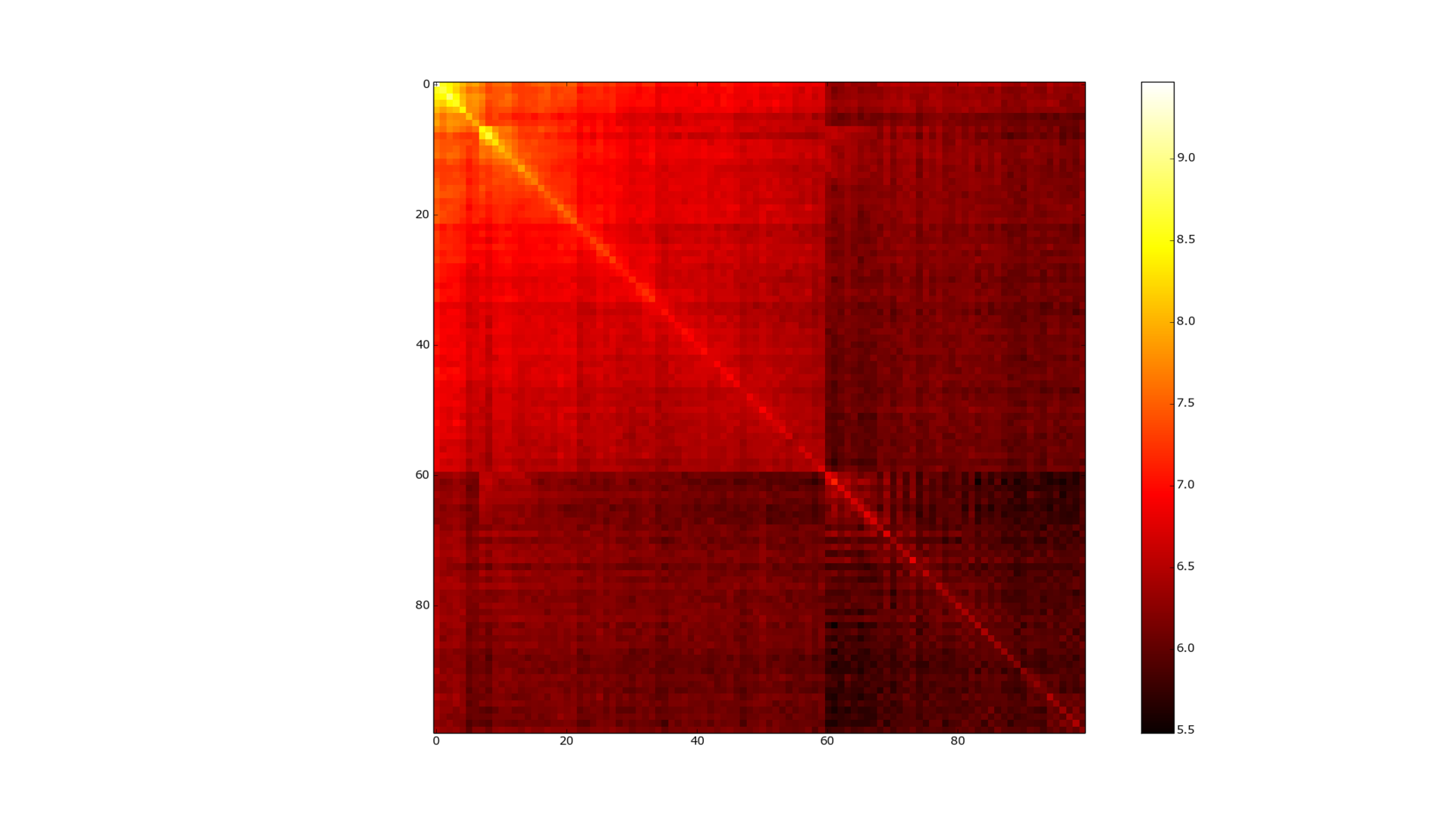
Figure 3. The adjacency matrix of the graph, vkontakte.
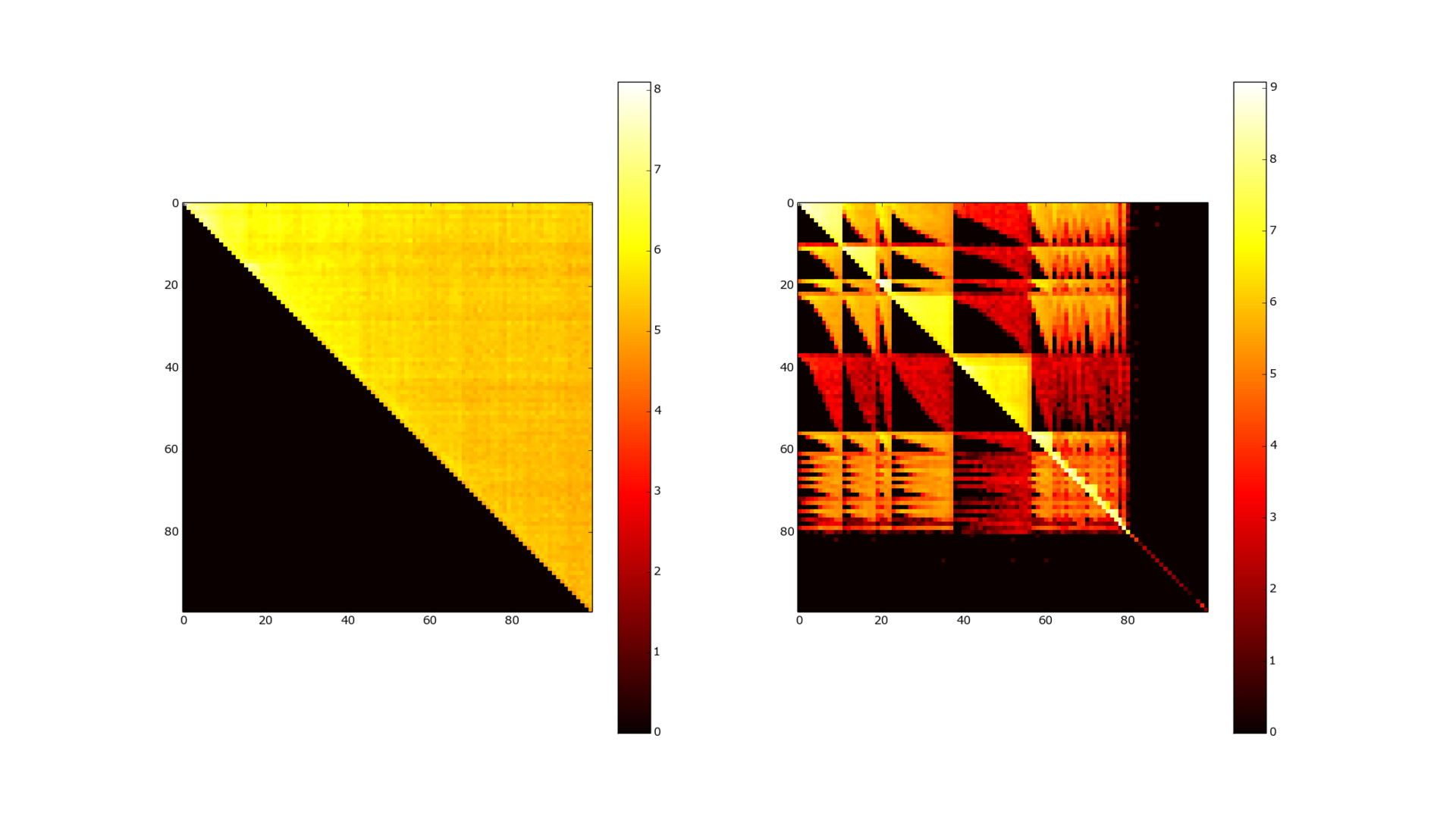
Figure 4. The adjacency matrix before and after clustering. 100k users.
In Figure 3, the adjacency matrix of the friend graph is presented, in a logarithmic form. She also does not inspire much hope for this kind of compression. The data looks much more interesting if in some way we pre-cluster our graph. Figure 4 shows the adjacency matrix after the MCL ( Markov Cluster Algorithm ) clustering pass. The correspondence matrix becomes almost diagonal (the color map is logarithmic, so bright yellow means more connections between elements by several orders of magnitude) - and WebGraph and many other algorithms are already excellent for compressing such data. (Asano [7] - currently being the best as far as I know from compression, but also the slowest in data access).
But the problem is that MCL is, at worst, cubic in time and quadratic in memory (http://micans.org/mcl/man/mclfaq.html#howfast). Everything in life is not so bad for symmetric graphs (which the social graph is almost like) - but it is still far from linearity. Another big problem is that the graph does not fit in the memory and it is necessary to invent distributed clustering techniques - and this is a completely different story. An interim solution to this problem was invented by Alberto Apostolico and Guido Drovandi [1] - re-numeration of the graph, simply passing through it search in width (BFS-search). This way, it is guaranteed that some vertices that link to each other will have close indices. In their work, they left GAP coding and replaced it with a rather complex model of reference coding, while receiving 1-3 bits per coding reference. In fact, the intuition is not very clear that BFS should correctly compose vertices, but this method works - I did this coding for the VK database and looked at the histogram for gaps (Figure 5) - it looks very promising. There are also suggestions to use Deep First Search instead of BFS, as well as more complex re-indexing schemes such as shingle reordering [7] - they give a similar increase. There is one more reason why BFS re-indexing should / can work - WebArchive databases are well encoded, and they are obtained just by sequential indexing of the live Internet graph.
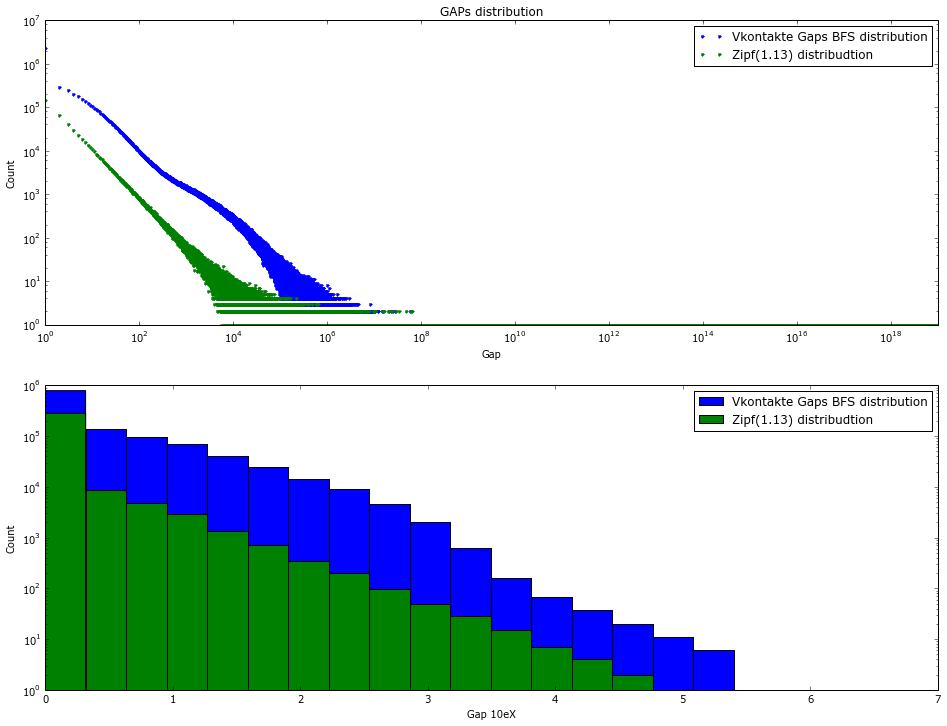
Figure 5. The distribution of gaps in the base of friends vkontakte after BFS indexing. 100k sample
Table 2. The distribution of gaps in the base of friends vkontakte after BFS indexing. 1M sample
The second work of Boldi and Vigna [5] is devoted to the theoretical justification of coding a list of gaps with various digital codes as well as comparing them with Huffmanman coding as possible upper bound. The basis is that the encoded value is distributed according to Zipf's law . The upper limit of compression for various alpha parameters turned out to be 4-13 bits per link. For the VKontakte database, this coding method gave 18 bits per link. Which, of course, is not bad and allows you to fit the entire database in RAM, but very far from the terratic estimates given in the works. Figure 5 shows a comparison of the gap distribution after BFS indexing, with the zipf distribution as close as possible to practical data (alpha = 1.15). Figure 6 shows the adjacency matrix for the graph after BFS reindexing - it reflects the reason for poor compression well - the diagonal is well drawn but the overall noise is still very large compared to the clustered matrix. These "bad" results are also confirmed by the work [6].
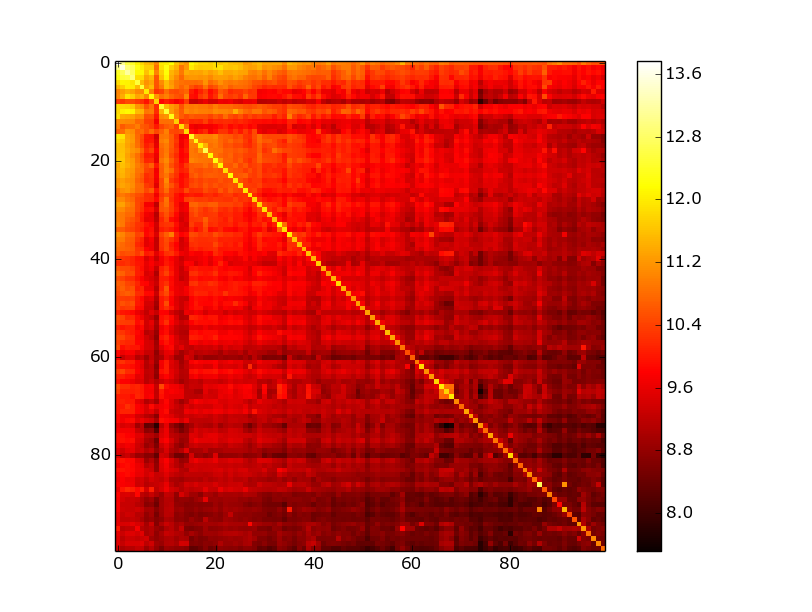
Figure 6. The adjacency matrix of the vkontakte base. After BFS re-indexing.
There is another method worthy of special attention - the exploitation of properties of the graph. Namely, the allocation of biklik (Bipartite graph) and the generation of a virtual vertex connecting the 2 parts of the subgraph. This allows you to reduce the length of the list of vertices for each side of the bichromatic graph. This problem is generally NP-complete, but there are many good heuristics for finding dicotyledonous subgraphs. This method was proposed in [9], as well as the BV algorithm gave rise to many others [10–11] and deserves more detailed consideration. Figure 6 describes only its main idea.
Figure 6. Biclik coding.
Most of the algorithms on graphs are well studied and designed on the basis of the fact that random access to graph elements is possible, at the moment the size of social graphs exceed the average RAM of the average machine in size, but at the same time easily fit on the hard disk. A compromise option is to compress the data with the ability to quickly access certain queries. We will focus on two:
a) get a list of edges for a particular vertex
b) find out if 2 vertices are connected.
Modern algorithms allow compressing data up to 1-5 bits per link, which makes it possible to work with a similar database on an average machine. I was inspired to write this article precisely the desire to fit the base of vkontakte friends in 32GB of RAM, given that now there are about 300M accounts with an average peak level of about 100, it seems quite realistic. It is on this basis that I will conduct my experiments.
')
The general properties of the graphs of interest to us are:
a) the fact that they are large, 16 - 19 or more tops and about 19 edges - which makes it impossible to work with them directly in memory, but allows you to store them even on one hard drive without any problems. The site law.di.unimi.it/datasets.php presents the entire vast range of such databases.
b) the distribution of degrees (vertices) of vertices, and indeed, all important frequency characteristics are described by a power dependence (Power-Law) at least asymptotically.
c) they are sparse. The average degree of the vertex is ~ 100-1000.
d) vertices are similar - the probability that you have a common friend is more for the connected vertices.
Boldi and Vigna.
In this paper, the graph in the "natural", uncompressed form will be represented by an array of lists:
node1 -> link11,link12,link13... node2 -> link21,link22,link23.... .... link[i,j] < link[i,j+1]. | Vertex | Degree of vertex | Ribs |
|---|---|---|
| 15 | eleven | 13,15,16,17,18,19,23,24,203,315,1034 |
| sixteen | ten | 15,16,17,22,23,24,315,316,317,3041 |
| 17 | 0 | |
| 18 | five | 13,15,16,17,50 |
Table 1. Natural coding of the graph. (Example taken from [2])
Let's call the difference between the indices of the two links “gap”.
Gap[i,j] = link[i,j-1] - link[i,j] The first of the families of compression algorithms are methods that use the following 2 basic approaches:
a) Exploitation of locality of vertices. Vertices more often refer to “close” peaks, rather than to “far” ones.
b) Operation of vertex similarity. “Close” vertices refer to the same vertices.
In these two statements lies a paradox - the term “proximity” of peaks can be described in the same way through similarity, then our statements will turn into a truism. It is in clarifying the concept of "proximity" that is the main difference between the algorithms I have tried.
The first work on this topic is apparently K. Randall [1]. It examined the web graph of Altavista still alive, and it was discovered that most of the links (80%) on the graph are local and have a large number of common links, and it was suggested to use the following reference coding:
- the new vertex is encoded as a link to a “similar” + list of additions and deletions, which in turn is encoded with gaps + nibble coding.
The guys squeezed the altavist to 5 bits per link (I will try to bring the worst compression results in the works). This approach has been greatly developed in the works of Paolo Boldi and Sebastiano Vigna.
They proposed a more complex method of reference coding, presented in Table 2. Each vertex can have one reference to “similar”, RefNr encodes the difference between the current vertex and it, if RefNr is zero, then the vertex has no reference. Copy list is a bit-list that encodes which vertices must be picked up by reference - if the corresponding Copy list bit is 1, then this vertex also belongs to the encoded one. Then Copylist is also encoded with RLE by a similar algorithm and turns into CopyBlocks:
01110011010 -> 0,0,2,1,1,0,0 We write the length - 1 for each repeating block + value of the first block (1 or 0), and the zeros remaining at the end can be discarded.
The rest of the vertices is converted into gaps, the intervals of zeros are coded separately (here a special property of web graphs is exploited, which will be discussed below) and the remaining gaps (Residuals) are recorded by one of the digitized codes ( Golomb , Huffman extremum).
As can be seen from table 2, this encoding can be multi-level - the degree of this multi-level is one of the parameters of the encoder L , with a large L, the encoding speed and decoding decreases, but the degree of compression increases.
| Vertex | Degree of vertex | Refnr | number of copy-blocks | Copy blocks | Number of intervals | intervals (relative left index) | spacing lengths | residue (Residual) |
|---|---|---|---|---|---|---|---|---|
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 15 | eleven | 0 | 2 | 0.2 | 3.0 | 5,189,11,718 | ||
| sixteen | ten | one | 7 | 0,0,2,1,1,0,0 | one | 600 | 0 | 12,3018 |
| 17 | 0 | |||||||
| 18 | five | 3 | one | four | 0 | 50 | ||
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
Table 2. The method of reference coding proposed by Boldi and Vigna for data from Table 1. [2]
The distribution of Gaps in the crawler bases is also subject to Power-Law law.

Figure 1. Distribution of "Gaps" in snapshot on .uk sites - 18.5M pages.
What allowed us to say "close" accounts are given to us from above in the form of ordered data from webcrawlers. And then develop the work on the above two directions: encode the list of edges as a modification of one of the previous vertices (reference coding), store the list of edges as “Gaps” (Gap [i, 0] = Node [i] - link [i, 0]) - and, using the frequency response identified above - to encode this list with one of the many integer codes. I must say that they did well: 2-5 bit per link [4]. In [2] and [3], even simpler reference coding methods LM and SSL are proposed that encode the data in small blocks. The result is superior or rather commensurate with the BV algorithm. From myself I want to add that even a simple coding with gaps gives a comparable result on Web - bases and at the same time all methods using local "similarity" noticeably succumb to social bases.
In social graphs, this effect does not seem to be observed — in Figure 2, the distribution of gaps in different pieces of the vkontakte database is presented. It is interesting that for the first million log / log accounts, the law for gaps is actually implemented. But with the increase in the amount of data. The distribution of gaps is becoming more and more "white."
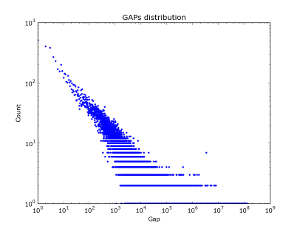 | 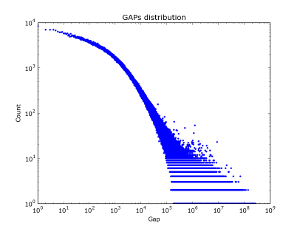 | 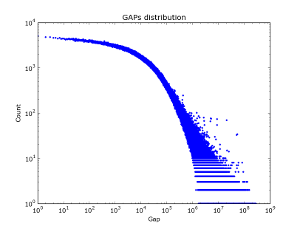 |
| Sample 50k. | Sampling 100k. | Sample 2M. |
Figure 2. The distribution of gaps in the base of friends vkontakte.

Figure 3. The adjacency matrix of the graph, vkontakte.

Figure 4. The adjacency matrix before and after clustering. 100k users.
In Figure 3, the adjacency matrix of the friend graph is presented, in a logarithmic form. She also does not inspire much hope for this kind of compression. The data looks much more interesting if in some way we pre-cluster our graph. Figure 4 shows the adjacency matrix after the MCL ( Markov Cluster Algorithm ) clustering pass. The correspondence matrix becomes almost diagonal (the color map is logarithmic, so bright yellow means more connections between elements by several orders of magnitude) - and WebGraph and many other algorithms are already excellent for compressing such data. (Asano [7] - currently being the best as far as I know from compression, but also the slowest in data access).
But the problem is that MCL is, at worst, cubic in time and quadratic in memory (http://micans.org/mcl/man/mclfaq.html#howfast). Everything in life is not so bad for symmetric graphs (which the social graph is almost like) - but it is still far from linearity. Another big problem is that the graph does not fit in the memory and it is necessary to invent distributed clustering techniques - and this is a completely different story. An interim solution to this problem was invented by Alberto Apostolico and Guido Drovandi [1] - re-numeration of the graph, simply passing through it search in width (BFS-search). This way, it is guaranteed that some vertices that link to each other will have close indices. In their work, they left GAP coding and replaced it with a rather complex model of reference coding, while receiving 1-3 bits per coding reference. In fact, the intuition is not very clear that BFS should correctly compose vertices, but this method works - I did this coding for the VK database and looked at the histogram for gaps (Figure 5) - it looks very promising. There are also suggestions to use Deep First Search instead of BFS, as well as more complex re-indexing schemes such as shingle reordering [7] - they give a similar increase. There is one more reason why BFS re-indexing should / can work - WebArchive databases are well encoded, and they are obtained just by sequential indexing of the live Internet graph.

Figure 5. The distribution of gaps in the base of friends vkontakte after BFS indexing. 100k sample
| Gap | amount | Share |
|---|---|---|
| one | 83812263 | 7.69% |
| 2 | 12872795 | 1.18% |
| 3 | 10643810 | 0.98% |
| four | 9097025 | 0.83% |
| five | 7938058 | 0.73% |
| 6 | 7032620 | 0.65% |
| 7 | 6322451 | 0.58% |
| eight | 5733866 | 0.53% |
| 9 | 5230160 | 0.48% |
| ten | 4837242 | 0.44% |
| top10 | 153520290 | 14.09% |
Table 2. The distribution of gaps in the base of friends vkontakte after BFS indexing. 1M sample
The second work of Boldi and Vigna [5] is devoted to the theoretical justification of coding a list of gaps with various digital codes as well as comparing them with Huffmanman coding as possible upper bound. The basis is that the encoded value is distributed according to Zipf's law . The upper limit of compression for various alpha parameters turned out to be 4-13 bits per link. For the VKontakte database, this coding method gave 18 bits per link. Which, of course, is not bad and allows you to fit the entire database in RAM, but very far from the terratic estimates given in the works. Figure 5 shows a comparison of the gap distribution after BFS indexing, with the zipf distribution as close as possible to practical data (alpha = 1.15). Figure 6 shows the adjacency matrix for the graph after BFS reindexing - it reflects the reason for poor compression well - the diagonal is well drawn but the overall noise is still very large compared to the clustered matrix. These "bad" results are also confirmed by the work [6].

Figure 6. The adjacency matrix of the vkontakte base. After BFS re-indexing.
Bikliki
There is another method worthy of special attention - the exploitation of properties of the graph. Namely, the allocation of biklik (Bipartite graph) and the generation of a virtual vertex connecting the 2 parts of the subgraph. This allows you to reduce the length of the list of vertices for each side of the bichromatic graph. This problem is generally NP-complete, but there are many good heuristics for finding dicotyledonous subgraphs. This method was proposed in [9], as well as the BV algorithm gave rise to many others [10–11] and deserves more detailed consideration. Figure 6 describes only its main idea.
 | 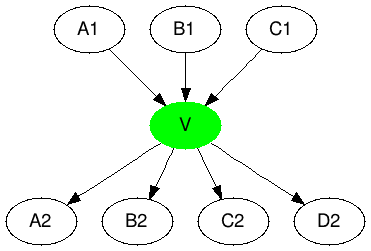 |
| A1 -> A2 B2 C2 D3 B1 -> A2 B2 C2 D4 C1 -> A2 B2 C2 D5 | A1 -> V D3 B1 -> V D4 C1 -> V D5 V -> A2 B2 C2 |
Figure 6. Biclik coding.
Literature
- A. Alberto and G. Drovandi: Graph compression by BFS.
- Sz. Grabowski and W. Bieniecki: Tight and simple Web graph compression.
- Sz. Grabowski and W. Bieniecki Merging adjacency lists for efficient Web graph compression
- P. Boldi and S. Vigna: The webgraph framework I: Compression techniques.
- P. Boldi and S. Vigna: The webgraph framework II: Codes for the World-Wide-Web. WebGraphII.pdf
- P. Boldi and S. Vigna. Permuting Web and Social Graphs.
- Flavio Chierichetti, Ravi Kumar. On Compressing Social Networks.
- Y. Asano, Y. Miyawaki, and T. Nishizeki: Efficient compression of web graphs.
- Gregory Buehrer, Kumar Chellapilla. A Scalable Pattern Mining Approach to Web Graph Compression with Communities
- Cecilia Hernandez, Gonzalo Navarro. Compressed Representations for Web and Social Graphs.
- F. Claude and G. Navarro: Fast and compact web graph representations.
Source: https://habr.com/ru/post/246325/
All Articles