Turing A-Machine and Hoara Pit-Stop Coffee Machine

Anyone who relies on practice, without knowing the theory, is like a helmsman entering a ship without a rudder or compass — he does not know where he is going.
Leonardo da Vinci

In the Sacred Language Wars, the final argument is often cited - since languages ​​are Turing-full, they are equivalent. Under the cat an attempt to clarify this thesis for those who have already coped with Python and now plans to study Erlang or Haskell according to the specification. Material survey, not methodical with pictures .

Alan Turing built his a-car in 1936.

"... the endless tape is divided into areas marked with symbols. At any time, exactly one symbol is available to the machine. The state of the machine depends on the available symbol and the machine is free to change this symbol. Inaccessible symbols on the tape do not affect the behavior of the machine. However , this is an elementary operation for a machine. Thus, any symbol has a chance ... "

1948 essay, Intelligent Machinery Turing.

We can say that the state machine is hidden in the machine, so it will be more understandable to the practitioners.
A constructor from which it is possible to assemble any a-machine is considered Turing complete. Two machines are considered Turing equivalent if one can be assembled with the other from the details of one.
Turing prototyped a universal unit capable of replacing an arbitrary a-machine. The Universal Turing Machine achieves this by simply reading a description of some private a-machine from the tape along with the data. Any two UMTs are obviously equivalent. And in 1946, von Neumann built this prototype. It is worth noting here that the UMT is a logarithmically slow private a-machine on complex calculations.
Turing with Church was postulated: any function of natural numbers is computable by a person equipped with paper and pencil if and only if the Universal Turing Machine handles it.
It follows from the above - steeper than the Universal Turing Machine, nothing can be. Whatever the system, all the same UMT succeed (if the thesis of Church-Turing is correct). Nevertheless, Turing had to admit that his car was without brakes. Because of Gödel's incompleteness theorem, the problem of stopping arises. You can not be sure that the UMT will always reach the state of Stop.
Calculations in UMT is a sequence of steps on the tape and state changes.
For example, the integer module abs (int) in assembly language can be taken as

cdq ;        eax  edx ; if eax>=0 then edx:=0 else edx:=0xFFFFFFFF xor eax, edx ;   XOR  ,      A ⊕ 0 = A ; XOR c -1   NOT A ⊕ –1 = ¬A ; if eax>=0 then eax:=eax xor 0=eax else eax:=eax xor 0xFFFFFFFF=not eax sub eax, edx ;    edx  eax ;  eax , edx=0      ;   eax    1   -eax ; ¬A + 1 = –A ; if eax>=0 then eax:=eax xor 0 - 0=eax else eax:=(eax xor -1) - (-1=not eax + 1= -eax 

Imperative programming languages ​​with if and goto implement Universal Turing Machine.

In the same year, 1936, Alonzo Church presented the lambda calculus to the world described by the three simple rules on their terms. (In general, Church’s research dates from 1928–1930, and Turing was a graduate student at Church, and yet his work was published at the same time.)
• The variables x, y, z ... are terms. (Alphabet)
• If M and N are terms, then (MN) –terms. (Application)
• If x is a variable and M is a term, then (λx.M) is a term. (Abstraction)
Well, it also clarifies that everything else is not lambda terms at all.
The abstraction here is a way to describe a function. Application - the ability to apply it to the arguments. Lambda expression can be perfectly represented by a tree.

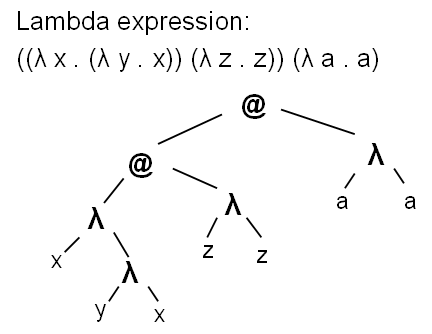
To enliven these non-contradictory rules, three types of reduction (simplification) of lambda expressions are introduced.

• α-conversion: rename argument (alpha); λx.x → λy.y
• β-reduction: applying the function to the arguments (beta); ((λn.n * 2) 7) → 7 * 2
• η-conversion: substitution equivalent (eta). λx. (fx) → f

Note that you can reduce in any order and get an equivalent result.

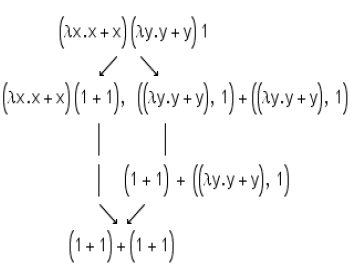
When an expression cannot be reduced, it is considered computed and in normal form. Calculations are a sequence of simplifications.
In 1958, John McCarthy implements lambda calculus in Lisp capable of being run on a von Neumann machine. Lisp is the implementation of lambda calculus and not the Turing machine (it does not have a goto), but according to Church-Turing thesis, it is such a machine. A novice beginner to practice Lisp should first realize that the sequence of actions of a program in a functional language is generally unknown to us and is not important, as the sequence of simplifications applied by the calculator to the lambda expression is not important. The representation of code and data in Lisp is uniform: it is a list defined by three operations.

 (defun cons (ab) (lambda (f) (funcall fab))) (defun car (c) (funcall c (lambda (ab) a))) (defun cdr (c) (funcall c (lambda (ab) b))) 

and the stack can be described like this

 (let (stack) (defun push (x) (setq stack (cons x stack))) (defun pop () ;; note the usefulness of VALUES. (values (car stack) (setq stack (cdr stack))))) 

Yes, the lambda calculus Turing is equivalent, but not the type. Introducing the restriction of the types of terms, although we generalize the formalism, but at the same time, we detract from the general concept of the term. Typed lambda calculus is generally not Turing complete.
')
To achieve completeness, additional abstractions are needed. And in 1942-1945, Eilenberg and MacLaine create such an abstraction - the theory of categories. Church calls category theory

the highest mathematical formalism of all that he had to see

Category C must contain
class ob (X) category objects
class H (A, B) morphisms (or arrows f: a-> b)
double operation ∘, composition of morphisms  f∘g, f∊H (B, C) g∊H (A, B) → f∘g∊H (A, C)

• associative: h ∘ (g ∘ f) = (h ∘ g) ∘ f
• and identified id: x → x
  id ∘ f = f = f ∘ id.

Functors are categories mappings that preserve structure.

Natural transformation is the ratio of two functors.

In the early 1970s, Girard and Reynolds independently formulated System-F as a polymorphic lambda calculus (by and large, they allowed a universal quantifier in lambda notation). Hindley and Milner developed the type-W algorithm of complexity O (1), that is, linear with the size of the expression (for this it was necessary to make the notation prefix). Milner builds the system into the ML language and by 1990 it appears in Haskell. Thus, in Haskell, you have a category Hask containing objects with all data types and morphisms all possible functions.
The concept of Haskell reflects the idea of ​​the mathematician Haskell Curry, who wrote that

proof is a program, and the formula being proved is a type of program

Computations in such a formalism are, say, the inference of the declared category, and the result of the calculations is regarded as a side effect of the proof.
For example, for exponential exponential series

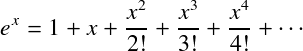
we can say

 integral fs = 0 : zipWith (/) fs [1..] --  (Fractional a, Enum a) => [a] -> [a] expx = 1 + (integral expx) --   

Algorithm-W and still elegant mathematical focus - monad, as a generalization of the structural recursion allowed to realize the category Hask on von Neumann machines. Haskell is Turing-complete if only because its type-checker is full of the W-implementing algorithm. But it should be understood that the language was not designed as a Turing machine, in the category theory there simply is no abstraction of the state on which the finite automata are built.
In practice, the Haskell student needs to get used to reasoning about the types of variables and the morphisms between them, rather than the values ​​(which are constant).

Von Neumann's machine is a sequential calculator, but the machines have learned how to connect in a network. In 1985, Charles Hoar publishes the document Communicating Sequential Processes, in which he develops a new formalism. The preface is written by Dijkstra.
The object is described in the alphabet of events in which it is involved. The combination of such events form the process.
Take a queuing machine

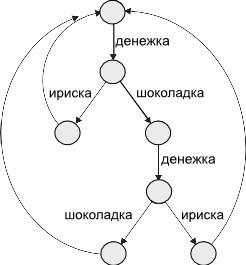
Let x be the event, and P is the process, then:

 (x → P ) 

(pronounced "x then P") describes an object that first makes an event x, and then behaves like P.

  = μX •  → ( → X |  → X) 

where X is a local variable that can be changed
The sequence of events passed by the object is the process trace.
The process environment is also seen as a sequential process.
Two processes may have the same event in the alphabet.

  = μX •( → X |  → X |  →  → X ) 

Sweet tooth is not averse to getting toffee for free, but miracles do not happen

 ( ||  ) = μ X • ( →  → X) 

In such a notation, Hoar builds algebra capable of effectively solving (at least diagnosing) the 'Problem of the dining philosophers' and deduces the laws of this algebra.

 L1 P||Q=Q||P L2 P ||(Q ||R)=(P ||Q)||R L3 (c →P)||(c →Q)=(c →(P ||Q)) ... 

The formalism is implemented in the Erlang, Golang, Ada Haskell libraries and other languages.
Are the two Turing machines seated on one tape a Turing machine?

Yes, Hoar answers. He declares his algebra in terms of lambda calculus and implements in Lisp. Now it has been agreed that interacting sequential processes can always be trivially represented by one running on a von Neumann machine. The inverse problem, the selection in the process of two interacting - is by no means trivial.
This is how a competitive sieve for Go’s first ten primes can look like

 package main //  2, 3, 4, ...   'ch'. func Generate(ch chan<- int) { for i := 2; ; i++ { ch <- i // ,       . } } //    in   out, //    'prime'. func Filter(in <-chan int, out chan<- int, prime int) { for { i := <-in //   'in'. if i%prime != 0 { out <- i //  'i'  'out'. } } } func main() { ch := make(chan int) //   ch. go Generate(ch) //  Generate  . for i := 0; i < 10; i++ { prime := <-ch print(prime, "\n") ch1 := make(chan int) go Filter(ch, ch1, prime) // Filter  . ch = ch1 } } 

From a practical point of view, programming concurrently in Erlang, Go, or just for the web, it is important to first decide on the common alphabet (shared resources) of processes. Languages ​​having tools for parallel programming provoke this tool to use. It should be remembered at the same time that any algorithm can be implemented consistently and, as a rule, more efficiently.

So, yes - the described formalisms are Turing equivalent. However, in imitation of Turing, proving this with each program by reconstructing one paradigm within the framework of another seems to me counterproductive. With their charter in a strange monastery do not go. By adopting a language professing a fundamentally different model of computation, one has to revise stable skills, metrics and design patterns.