Data structures: 2-3 heap (2-3 heap)
The question of an effective way to implement a queue with a priority by some data structure remains relevant for a long time. The answer to this question is always a kind of compromise between the amount of memory needed to store data and the time it takes to work on a queue.
In computer science, heap structures are used to efficiently implement a priority queue.
A heap is a specialized tree-type data structure that satisfies the heap property: if B is a descendant node of node A , then key ( A ) ≥ key ( B ). It follows that the element with the largest key is always the root node of the heap, therefore sometimes such heaps are called max-heaps (alternatively, if the comparison is turned over, the smallest element will always be the root node, such heaps are called min-heaps). There is no limitation on how many descendant nodes each heap node has, although in practice their number is usually not more than two. Heaps are crucial in some efficient algorithms on graphs, such as the Dijkstra algorithm and the pyramid sorting.
One of the most studied and well-established data structures for storing and working with priority queues are the Binary Heap and the Fibonacci Heap . But these structures have some peculiarities.
')
For example, a binary heap for basic operations has a laboriousness of Θ (logn), besides finding the minimum, and merging such heaps will require linear time (!). But to store such a heap, you need little memory compared to other heaps.
The Fibonacci heap is balanced when the node is removed from the heap, which reduces the complexity of the basic operations. With a large number of consecutive operations of adding the Fibonacci heap grows in width and balancing occurs only with the operation of removing the minimum, so the operation of obtaining the minimum may require a significant investment of time!
Tadao Takaoka took up the solution to this problem by publishing his work “2-3 heap” in 1999 ...
A 2-3 heap (2-3 heap) is a tree-type data structure that satisfies the heap property (min-heap, max-heap). It is an alternative to the Fibonacci heap (Fibonacci heap). Consists of 2-3 trees.
The solution that offers 2-3 heap, is that, unlike Heap Fibonacci, 2-3 heap balances not only when you delete, but also when adding new elements, reducing the computational load when removing the minimum node from the heap.
The number of children of the vertex t of an arbitrary tree T is called the degree of this vertex, and the degree of the tree is the degree of its root.
2-3 trees are trees T 0 , T 1 , T 2 , ..., defined inductively. The tree T 0 consists of a single vertex. A tree T i is a tree composed of either two trees T i-1 or three: the root of each next one becomes the rightmost child of the previous one.
Trees with 2-3 heaps we call trees H [ i ]. The tree H [ i ] is either an empty 2-3 tree, or one, or two 2-3 trees of degree i , connected by the same way as trees T i .
2-3 heap is an array of trees H [ i ] ( i = 0..n), for each of which the heap property is satisfied.
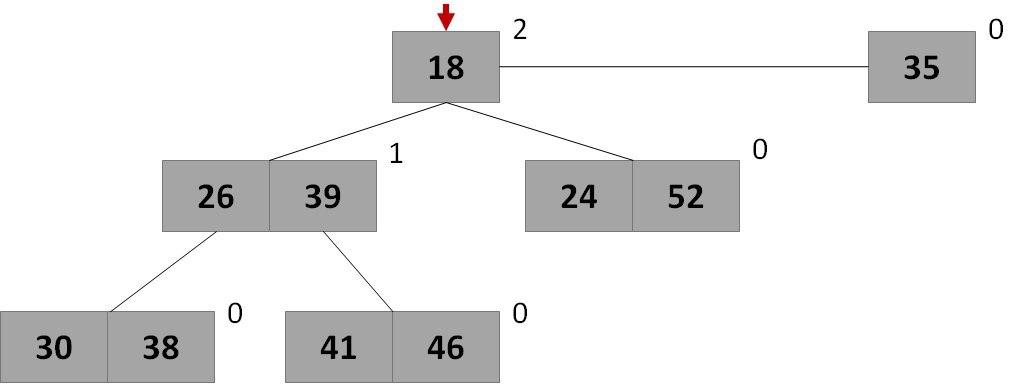
rice Heap view
The minimum element of the heap is at the root of one of the heap trees. To find the minimum node, you need to walk through the trees.
By supporting a pointer to the minimum node in the heap, we can find this node in constant time (Θ (1))
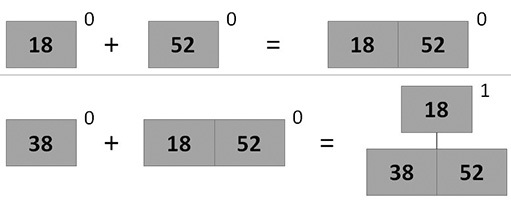

rice Animation of sequential addition of elements in 2-3 heap
The minimal element of the heap is in the root of one of the heap trees, let's say in H [ i ] - we will find it using FindMin. Extract the H [ i ] tree from the heap and delete its root, and the tree will split into subtrees, which we will later add to the heap.
We will delete the root recursively: if the tree consists of one vertex, then simply remove it; otherwise, disconnect from the root of the rightmost child and continue the removal.
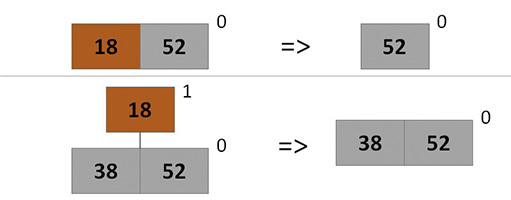
First of all, we can freely reduce the key at the required node. After that, you need to check: if the node is in the root of the tree, then nothing else needs to be done, otherwise you will need to remove this node with all the subtrees and insert it back into the heap (with the key already changed).

There are two heaps that need to be merged into one. To do this, we will in turn extract all 2-3 trees from the second heap and insert them into the first heap. After it will be necessary to correct the counter of the number of nodes: we summarize the number of elements in the first and second heaps and write the result in the counter in the first heap, and in the second heap we set the counter to 0.
The table shows the complexity of operations queue with priority (in the worst case, worst case)
The symbol '*' denotes the amortized complexity of operations
Thank you for your attention!
The source code of a C ++ implementation based on the author’s article 2-3 Heap is available on GitHub under MIT.
PS: When writing a course project on this topic, I realized that there was practically no information in RuNet, so I decided to deposit my couple of kopecks in this case, telling the interested community about this algorithm.
In computer science, heap structures are used to efficiently implement a priority queue.
A heap is a specialized tree-type data structure that satisfies the heap property: if B is a descendant node of node A , then key ( A ) ≥ key ( B ). It follows that the element with the largest key is always the root node of the heap, therefore sometimes such heaps are called max-heaps (alternatively, if the comparison is turned over, the smallest element will always be the root node, such heaps are called min-heaps). There is no limitation on how many descendant nodes each heap node has, although in practice their number is usually not more than two. Heaps are crucial in some efficient algorithms on graphs, such as the Dijkstra algorithm and the pyramid sorting.
One of the most studied and well-established data structures for storing and working with priority queues are the Binary Heap and the Fibonacci Heap . But these structures have some peculiarities.
')
For example, a binary heap for basic operations has a laboriousness of Θ (logn), besides finding the minimum, and merging such heaps will require linear time (!). But to store such a heap, you need little memory compared to other heaps.
The Fibonacci heap is balanced when the node is removed from the heap, which reduces the complexity of the basic operations. With a large number of consecutive operations of adding the Fibonacci heap grows in width and balancing occurs only with the operation of removing the minimum, so the operation of obtaining the minimum may require a significant investment of time!
Tadao Takaoka took up the solution to this problem by publishing his work “2-3 heap” in 1999 ...
A little about the structure of "2-3 Heap"
A 2-3 heap (2-3 heap) is a tree-type data structure that satisfies the heap property (min-heap, max-heap). It is an alternative to the Fibonacci heap (Fibonacci heap). Consists of 2-3 trees.
The solution that offers 2-3 heap, is that, unlike Heap Fibonacci, 2-3 heap balances not only when you delete, but also when adding new elements, reducing the computational load when removing the minimum node from the heap.
The number of children of the vertex t of an arbitrary tree T is called the degree of this vertex, and the degree of the tree is the degree of its root.
2-3 trees are trees T 0 , T 1 , T 2 , ..., defined inductively. The tree T 0 consists of a single vertex. A tree T i is a tree composed of either two trees T i-1 or three: the root of each next one becomes the rightmost child of the previous one.
Trees with 2-3 heaps we call trees H [ i ]. The tree H [ i ] is either an empty 2-3 tree, or one, or two 2-3 trees of degree i , connected by the same way as trees T i .
2-3 heap is an array of trees H [ i ] ( i = 0..n), for each of which the heap property is satisfied.

rice Heap view
Node structure
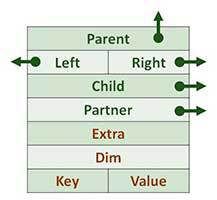 | Each node has pointers to other nodes (fields with arrows), service fields and a pair of key (priority) - value. |
Basic operations
Find the minimum in 2-3 heap (FindMin)
The minimum element of the heap is at the root of one of the heap trees. To find the minimum node, you need to walk through the trees.
By supporting a pointer to the minimum node in the heap, we can find this node in constant time (Θ (1))
Insert in 2-3 heap (Insert)
- To add a new element, create a tree H [0] containing one vertex
- Perform the operation of adding this tree to the heap. When adding a tree of degree i to the heap, the following options are possible:
- If there is no tree with such priority, then simply add it to the heap.
- Otherwise, we extract such a tree from the heap and combine it with the added one, then add the resulting tree to the heap.
- After adding we fix the pointer to the minimum root


rice Animation of sequential addition of elements in 2-3 heap
Remove the minimum item from the heap
The minimal element of the heap is in the root of one of the heap trees, let's say in H [ i ] - we will find it using FindMin. Extract the H [ i ] tree from the heap and delete its root, and the tree will split into subtrees, which we will later add to the heap.
We will delete the root recursively: if the tree consists of one vertex, then simply remove it; otherwise, disconnect from the root of the rightmost child and continue the removal.

Decrease key at the element
First of all, we can freely reduce the key at the required node. After that, you need to check: if the node is in the root of the tree, then nothing else needs to be done, otherwise you will need to remove this node with all the subtrees and insert it back into the heap (with the key already changed).

Combining two heaps into one
There are two heaps that need to be merged into one. To do this, we will in turn extract all 2-3 trees from the second heap and insert them into the first heap. After it will be necessary to correct the counter of the number of nodes: we summarize the number of elements in the first and second heaps and write the result in the counter in the first heap, and in the second heap we set the counter to 0.
Comparison of the complexity of operations with other algorithms
The table shows the complexity of operations queue with priority (in the worst case, worst case)
The symbol '*' denotes the amortized complexity of operations
| Operation | Binary heap | Binomial heap | Fibonacci heap | 2-3 heap |
|---|---|---|---|---|
| Findmin | Θ (1) | O (logn) | Θ (1) * | Θ (1) * |
| DeleteMin | Θ (logn) | Θ (logn) | O (logn) * | O (logn) * |
| Insert | Θ (logn) | O (logn) | Θ (1) * | Θ (1) * |
| Decreasekey | Θ (logn) | Θ (logn) | Θ (1) * | Θ (1) * |
| Merge / union | Θ (n) | Ω (logn) | Θ (1) | Θ (1) * |
Thank you for your attention!
The source code of a C ++ implementation based on the author’s article 2-3 Heap is available on GitHub under MIT.
PS: When writing a course project on this topic, I realized that there was practically no information in RuNet, so I decided to deposit my couple of kopecks in this case, telling the interested community about this algorithm.
Source: https://habr.com/ru/post/246105/
All Articles