Working groups in OpenCL 2.0. Heterogeneous working groups
Among the new features of OpenCL 2.0, several new useful built-in functions have appeared, the so-called workgroup functions. These built-in functions provide widely used parallel primitives that operate at the workgroup level. This article briefly describes the workgroup functions, provides performance data for an OpenCL Intel HD Graphics device, and also discusses an example of using heterogeneous workgroups.
The functions of the working groups include three classical algorithms of the working group level ( value broadcast, reduce and scan ), as well as two built-in functions that check the logical result of the operation performed for the entire working group. The reduce and scan algorithms support operations add, min and max .
The functionality of the built-in workgroup functions is evident from the titles.
An important restriction regarding the listed built-in functions: they are valid only for scalar data types (for example, the popular types int4 and float4 are not supported). In addition, 8-bit data types, such as char or uchar, are not supported.
The functions of the working groups, as their name implies, always work in parallel for the whole working group. There is an implicit consequence from this: any call to the function of the working group acts as a barrier.
The use of workgroup functions involves two main ideas. First, the functions of the working groups are convenient. It is much easier to use one built-in function instead of writing a sufficiently large piece of code that would be required to implement the same functionality in OpenCL 1.2. Secondly, the functions of the working groups are more efficient from the point of view of productivity, since they use equipment optimization.
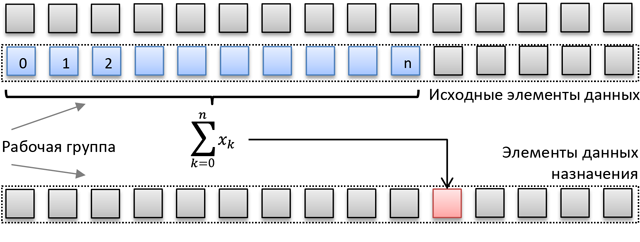
For example, consider the following task (which may be part of an algorithm): calculating the sums of prefixes for subordinate arrays of equal size of some larger array. So, we need to calculate the sum of the prefix for each element of each slave array and store it in the target memory area with the same markup. The source and target data layouts are shown in the following diagram.
')
A simple OpenCL kernel for this task may look like this:
The corresponding code is shown below.
Such a primitive approach is extremely inefficient in most cases (except for very small working groups). Obviously, the inner for () loop performs too many redundant load and add operations; This procedure can clearly be optimized. Moreover, with an increase in the size of the working group, redundancy also increases. More efficient use of Intel HD Graphics hardware resources requires a more efficient algorithm, such as Blelloch. We will not examine it in detail: it is wonderfully described in the classic GPU Gems article.
OpenCL 1.2 code with parallel scanning will look like this.
As a rule, such code works more efficiently and forms not so high load on hardware resources, but with some reservations.
In this code, there are costs for moving data between local and global memory, as well as some restrictions. To achieve really high efficiency, the algorithm requires a sufficiently large working group size. With small workgroups (<16), performance is unlikely to be higher than that of a simple cycle.
In addition, pay attention to the complexity of the code and additional logic designed to avoid conflicts in the common local memory (for example, the macro BANK_OFFSET ).
Using working groups allows you to bypass all the problems mentioned. The corresponding version of the optimized OpenCL code is shown below.
The performance results of both optimized algorithms are measured for a sufficiently large amount of input data (each working group scans 65,536 elements, which, depending on the local size, corresponds to 8192 ... 2048 iterations of the outer loop).

As expected, the simple cycle runs much slower as the local size increases, and the performance of both optimized variants increases.
If you set the optimal size of the working group for a given algorithm, then the kernel comparison will be like this.

Note that the use of work_group_scan_exclusive_add () significantly improves the productivity of a workgroup of any size and at the same time simplifies the code.
The OpenCL execution model includes the concept of working groups, which are groups of individual work items in the NDRange. If an application uses OpenCL 1.x, then the size of the NDRange should be completely (without remainder) divided by the size of the working groups. If the clEnqueueNDRangeKernel call includes global_size and local_size parameters that are not completely divisible, the call will return the error code CL_INVALID_WORK_GROUP_SIZE . If the clEnqueueNDRangeKernel call specifies a NULL value for the local_size parameter, allowing the executable module to choose the size of the workgroup, then the executable module will need to choose a size that can be used to completely divide the global NDRange sizes.
The need to choose such a size of working groups so that the size of the NDRange is completely divided into it may cause difficulties for developers. Consider a simple 3x3 image blur algorithm. In this algorithm, each output pixel is calculated as the average value for the input pixel values in the neighboring area of 3x3. The problem arises when processing the output pixels located on the image frame, since these pixels depend on the pixels outside the bounds of the input image.

In some applications, the input values of the frames do not matter, you can skip them. In this case, the size of the NDRange is the same as the size of the output image minus the frame area. This often turns out the size of NDRange, which is difficult to completely divide. For example, to apply a 3x3 filter to a 1920x1080 image, a frame is required that is one pixel thick on each side. The easiest way to do this is with the 1918x1078 kernel. But neither 1918 nor 1078 are divided completely into the values giving working groups of optimal size.
OpenCL 2.0 introduces a new feature that resolves the issues described in the previous section. We are talking about the so-called heterogeneous working groups: the OpenCL 2.0 executable module can divide the NDRange into non-uniform working groups in any dimension. If the developer specifies the size of the workgroup to which the size of the NDRange is not completely divided, the module being executed will divide the NDRange in such a way as to create as many workgroups as possible with the specified size, and the rest of the workgroups will have a different size.
Because of this, OpenCL can use workgroups of any size for any size of NDRange when the developer passes the NULL value of the local_size parameter to clEnqueueNDRangeKernel . In general, using the NULL value in the local_size parameter remains the preferred method for executing kernels, unless the logic of your application requires any particular size of workgroup.
Inside the kernel code, the built-in get_local_size () function returns the actual size of the workgroup from which it was called. If the kernel needs the exact size specified for the local_size parameter in clEnqueueNDRangeKernel , the built-in get_get_enqueued_local_size () function returns these values.
To enable the use of heterogeneous workgroups, you must compile the kernel with the -cl-std = CL2.0 flag , including this and other OpenCL 2.0 features. Without using this flag, the compiler will use OpenCL version 1.2, even if the device supports OpenCL 2.0. In addition, heterogeneous workgroups can be disabled for kernels compiled for the -cl-std = CL2.0 flag using the -cl-uniform-work-group-size flag. This can be useful for obsolete kernel code before fully switching to OpenCL 2.0.
The heterogeneous workgroup function in OpenCL 2.0 improves the ease of use of OpenCL and can improve the performance of some cores. Developers no longer add system and kernel code to work with NDRange sizes that are not completely divided. The code created to use this feature can effectively use SIMD and memory access alignment: these benefits are provided by the right choice of workgroup size.
In the code of the curriculum, the 3x3 blur algorithm described above is implemented. The most interesting part of the code is in the main.cpp file.
For each option in paragraphs. 5-8, the results of a call to get_local_size () and get_get_enqueued_local_size () in each of the four corners of the NDRange are displayed on the screen. Thus, we see how the NDRange is divided into working groups. The kernel that implements the blur algorithm is stored in BoxBlur.cl. It contains a very simple implementation, but is not the most effective way to apply blur.
To build and run this training program, you need a PC that meets the following requirements:
The training program is a console application that reads an input bitmap image and writes output raster images for each of the varieties of NDRange described in the section above. This training program supports several command line parameters: -h, -? (display of help text and output), -i <input prefix> (prefix of input bitmap image), -o <output prefix> (prefix of output bitmap image).
After starting the training program for the provided picture, the result will be as follows.
The input image has a size of 640x480, so the size of the NDRange in each case will be 638x478. The result above shows that running the OpenCL 1.2 kernel with the local_size parameter NULL forces you to use odd sizes for each workgroup (1, 239). Working group sizes that are not powers of two can work very slowly in some cores. SIMD conveyors may be idle, synchronous memory access may be impaired.
Running the OpenCL 1.2 kernel with the specified workgroup size (16x16) gives an error, since neither 648 nor 478 are completely divided by 16.
Running the OpenCL 2.0 kernel with the local_size parameter NULL value allows the OpenCL module to split the NDRange into workgroups of any size. The above is the result: it can be seen that the executable module continues to use the uniform size of the working groups in the same way as for the OpenCL 1.2 core.
Running an OpenCL 2.0 kernel with a given workgroup size (16x16) will result in the NDRange size being divided into heterogeneous workgroups. We see that the left upper working group has a size of 16x16, the upper right is 14x16, the lower left is 16x14, and the lower right is 14x14. Since in most cases the size of the working group is 16x16, this core will use SIMD pipelines very efficiently and memory access will be very fast.
Full versions of articles on the IDZ website:
Original articles in English:
Description of the functions of the working groups
The functions of the working groups include three classical algorithms of the working group level ( value broadcast, reduce and scan ), as well as two built-in functions that check the logical result of the operation performed for the entire working group. The reduce and scan algorithms support operations add, min and max .
The functionality of the built-in workgroup functions is evident from the titles.
- work_group_broadcast () distributes the value of the selected work item to all members of the workgroup.
- work_group_reduce () calculates the values of sum, min or max for all elements of the working group, and then distributes the resulting value to all elements of the working group.
- work_group_scan () calculates the values of sum, min or max for all previous work items (with the possible inclusion of current ones).
- work_group_all () returns a logical AND for the same logical expression calculated for each work item.
- work_group_any () works in the same way as work_group_all () , but uses a logical OR.
An important restriction regarding the listed built-in functions: they are valid only for scalar data types (for example, the popular types int4 and float4 are not supported). In addition, 8-bit data types, such as char or uchar, are not supported.
The functions of the working groups, as their name implies, always work in parallel for the whole working group. There is an implicit consequence from this: any call to the function of the working group acts as a barrier.
The use of workgroup functions involves two main ideas. First, the functions of the working groups are convenient. It is much easier to use one built-in function instead of writing a sufficiently large piece of code that would be required to implement the same functionality in OpenCL 1.2. Secondly, the functions of the working groups are more efficient from the point of view of productivity, since they use equipment optimization.
For example, consider the following task (which may be part of an algorithm): calculating the sums of prefixes for subordinate arrays of equal size of some larger array. So, we need to calculate the sum of the prefix for each element of each slave array and store it in the target memory area with the same markup. The source and target data layouts are shown in the following diagram.

')
A simple OpenCL kernel for this task may look like this:
- each array (line in the illustration) will be processed by one working group;
- for each work item, the scan is performed using a simple for () loop for the preceding items, then the cumulative prefix value is added, and then the result is stored at the destination;
- if the size of the workgroup is smaller than the input array, then the source and destination indices are shifted by the size of the workgroup, the cumulative prefix is updated and this process is repeated until the end of the source line.
The corresponding code is shown below.
Code
__kernel void Calc_wg_offsets_naive( __global const uint* gHistArray, __global uint* gPrefixsumArray, uint bin_size ) { uint lid = get_local_id(0); uint binId = get_group_id(0); //calculate source/destination offset for workgroup uint group_offset = binId * bin_size; local uint maxval; //initialize cumulative prefix if( lid == 0 ) maxval = 0; barrier(CLK_LOCAL_MEM_FENCE); do { //perform a scan for every workitem uint prefix_sum=0; for(int i=0; i<lid; i++) prefix_sum += gHistArray[group_offset + i]; //store result gPrefixsumArray[group_offset + lid] = prefix_sum + maxval; prefix_sum += gHistArray[group_offset + lid]; //update group offset and cumulative prefix if( lid == get_local_size(0)-1 ) maxval += prefix_sum; barrier(CLK_LOCAL_MEM_FENCE); group_offset += get_local_size(0); } while(group_offset < (binId+1) * bin_size); } Such a primitive approach is extremely inefficient in most cases (except for very small working groups). Obviously, the inner for () loop performs too many redundant load and add operations; This procedure can clearly be optimized. Moreover, with an increase in the size of the working group, redundancy also increases. More efficient use of Intel HD Graphics hardware resources requires a more efficient algorithm, such as Blelloch. We will not examine it in detail: it is wonderfully described in the classic GPU Gems article.
OpenCL 1.2 code with parallel scanning will look like this.
Code
#define WARP_SHIFT 4 #define GRP_SHIFT 8 #define BANK_OFFSET(n) ((n) >> WARP_SHIFT + (n) >> GRP_SHIFT) __kernel void Calc_wg_offsets_Blelloch(__global const uint* gHistArray, __global uint* gPrefixsumArray, uint bin_size ,__local uint* temp ) { int lid = get_local_id(0); uint binId = get_group_id(0); int n = get_local_size(0) * 2; uint group_offset = binId * bin_size; uint maxval = 0; do { // calculate array indices and offsets to avoid SLM bank conflicts int ai = lid; int bi = lid + (n>>1); int bankOffsetA = BANK_OFFSET(ai); int bankOffsetB = BANK_OFFSET(bi); // load input into local memory temp[ai + bankOffsetA] = gHistArray[group_offset + ai]; temp[bi + bankOffsetB] = gHistArray[group_offset + bi]; // parallel prefix sum up sweep phase int offset = 1; for (int d = n>>1; d > 0; d >>= 1) { barrier(CLK_LOCAL_MEM_FENCE); if (lid < d) { int ai = offset * (2*lid + 1)-1; int bi = offset * (2*lid + 2)-1; ai += BANK_OFFSET(ai); bi += BANK_OFFSET(bi); temp[bi] += temp[ai]; } offset <<= 1; } // clear the last element if (lid == 0) { temp[n - 1 + BANK_OFFSET(n - 1)] = 0; } // down sweep phase for (int d = 1; d < n; d <<= 1) { offset >>= 1; barrier(CLK_LOCAL_MEM_FENCE); if (lid < d) { int ai = offset * (2*lid + 1)-1; int bi = offset * (2*lid + 2)-1; ai += BANK_OFFSET(ai); bi += BANK_OFFSET(bi); uint t = temp[ai]; temp[ai] = temp[bi]; temp[bi] += t; } } barrier(CLK_LOCAL_MEM_FENCE); //output scan result to global memory gPrefixsumArray[group_offset + ai] = temp[ai + bankOffsetA] + maxval; gPrefixsumArray[group_offset + bi] = temp[bi + bankOffsetB] + maxval; //update cumulative prefix sum and shift offset for next iteration maxval += temp[n - 1 + BANK_OFFSET(n - 1)] + gHistArray[group_offset + n - 1]; group_offset += n; } while(group_offset < (binId+1) * bin_size); } As a rule, such code works more efficiently and forms not so high load on hardware resources, but with some reservations.
In this code, there are costs for moving data between local and global memory, as well as some restrictions. To achieve really high efficiency, the algorithm requires a sufficiently large working group size. With small workgroups (<16), performance is unlikely to be higher than that of a simple cycle.
In addition, pay attention to the complexity of the code and additional logic designed to avoid conflicts in the common local memory (for example, the macro BANK_OFFSET ).
Using working groups allows you to bypass all the problems mentioned. The corresponding version of the optimized OpenCL code is shown below.
Code
__kernel void Calc_wg_offsets_wgf( __global const uint* gHistArray, __global uint* gPrefixsumArray, uint bin_size ) { uint lid = get_local_id(0); uint binId = get_group_id(0); uint group_offset = binId * bin_size; uint maxval = 0; do { uint binValue = gHistArray[group_offset + lid]; uint prefix_sum = work_group_scan_exclusive_add( binValue ); gPrefixsumArray[group_offset + lid] = prefix_sum + maxval; maxval += work_group_broadcast( prefix_sum + binValue, get_local_size(0)-1 ); group_offset += get_local_size(0); } while(group_offset < (binId+1) * bin_size); } The performance results of both optimized algorithms are measured for a sufficiently large amount of input data (each working group scans 65,536 elements, which, depending on the local size, corresponds to 8192 ... 2048 iterations of the outer loop).

As expected, the simple cycle runs much slower as the local size increases, and the performance of both optimized variants increases.
If you set the optimal size of the working group for a given algorithm, then the kernel comparison will be like this.

Note that the use of work_group_scan_exclusive_add () significantly improves the productivity of a workgroup of any size and at the same time simplifies the code.
Heterogeneous OpenCL 2.0 working groups
The OpenCL execution model includes the concept of working groups, which are groups of individual work items in the NDRange. If an application uses OpenCL 1.x, then the size of the NDRange should be completely (without remainder) divided by the size of the working groups. If the clEnqueueNDRangeKernel call includes global_size and local_size parameters that are not completely divisible, the call will return the error code CL_INVALID_WORK_GROUP_SIZE . If the clEnqueueNDRangeKernel call specifies a NULL value for the local_size parameter, allowing the executable module to choose the size of the workgroup, then the executable module will need to choose a size that can be used to completely divide the global NDRange sizes.
The need to choose such a size of working groups so that the size of the NDRange is completely divided into it may cause difficulties for developers. Consider a simple 3x3 image blur algorithm. In this algorithm, each output pixel is calculated as the average value for the input pixel values in the neighboring area of 3x3. The problem arises when processing the output pixels located on the image frame, since these pixels depend on the pixels outside the bounds of the input image.

In some applications, the input values of the frames do not matter, you can skip them. In this case, the size of the NDRange is the same as the size of the output image minus the frame area. This often turns out the size of NDRange, which is difficult to completely divide. For example, to apply a 3x3 filter to a 1920x1080 image, a frame is required that is one pixel thick on each side. The easiest way to do this is with the 1918x1078 kernel. But neither 1918 nor 1078 are divided completely into the values giving working groups of optimal size.
OpenCL 2.0 introduces a new feature that resolves the issues described in the previous section. We are talking about the so-called heterogeneous working groups: the OpenCL 2.0 executable module can divide the NDRange into non-uniform working groups in any dimension. If the developer specifies the size of the workgroup to which the size of the NDRange is not completely divided, the module being executed will divide the NDRange in such a way as to create as many workgroups as possible with the specified size, and the rest of the workgroups will have a different size.
Because of this, OpenCL can use workgroups of any size for any size of NDRange when the developer passes the NULL value of the local_size parameter to clEnqueueNDRangeKernel . In general, using the NULL value in the local_size parameter remains the preferred method for executing kernels, unless the logic of your application requires any particular size of workgroup.
Inside the kernel code, the built-in get_local_size () function returns the actual size of the workgroup from which it was called. If the kernel needs the exact size specified for the local_size parameter in clEnqueueNDRangeKernel , the built-in get_get_enqueued_local_size () function returns these values.
To enable the use of heterogeneous workgroups, you must compile the kernel with the -cl-std = CL2.0 flag , including this and other OpenCL 2.0 features. Without using this flag, the compiler will use OpenCL version 1.2, even if the device supports OpenCL 2.0. In addition, heterogeneous workgroups can be disabled for kernels compiled for the -cl-std = CL2.0 flag using the -cl-uniform-work-group-size flag. This can be useful for obsolete kernel code before fully switching to OpenCL 2.0.
The heterogeneous workgroup function in OpenCL 2.0 improves the ease of use of OpenCL and can improve the performance of some cores. Developers no longer add system and kernel code to work with NDRange sizes that are not completely divided. The code created to use this feature can effectively use SIMD and memory access alignment: these benefits are provided by the right choice of workgroup size.
In the code of the curriculum, the 3x3 blur algorithm described above is implemented. The most interesting part of the code is in the main.cpp file.
Code
//1. . //2. OpenCL C OpenCL 1.2. // Get the box blur kernel compiled using OpenCL 1.2 (which is the // default compilation, even on an OpenCL 2.0 device). This allows // the code to show the pre-OpenCL 2.0 behavior. cl::Kernel kernel_1_2 = GetKernel(device, context); //3. OpenCL C OpenCL 2.0 ( OpenCL 2.0). // Get the box blur kernel compiled using OpenCL 2.0. OpenCL 2.0 // is required in order to use the non-uniform work-groups feature. kernel_2_0 = GetKernel(device, context, "-cl-std=CL2.0"); //4. , . // Set the size of the global NDRange, to be used in all NDRange cases. // Since this is a box blur, we use a global size that is two elements // smaller in each dimension. This creates a range which often doesn't // divide nicely by local work sizes we might commonly pick for running // kernels. cl::NDRange global_size = cl::NDRange(input.get_width() - 2, input.get_height() - 2); //5. , OpenCL 1.2, local_size NULL. // Blur the image with a NULL local range using the OpenCL 1.2 compiled // kernel. cout << "Compiled with OpenCL 1.2 and using a NULL local size:" << end1 << end1; output = RunBlurKernel(context, queue, kernel_1_2, global_size, cl::NullRange, input, true); //6. , OpenCL 1.2, local_size 16x16. // Blur the image with an even local range using the OpenCL 1.2 // compiled kernel. This won't work, even if we are running on an // OpenCL 2.0 implementation. The kernel has to be explicitly compiled // with OpenCL 2.0 compilation enabled in the compiler switches. try { cout << "Compiled with OpenCL 1.2 and using an even local size:" << end1 << end1; output = RunBlurKernel(context, queue, kernel_1_2, global_size, cl::NDRange(16, 16), input, true); cout << end1; output.Write(output_files[1]); } catch (...) { cout << "Trying to launch a non-uniform workgroup with a kernel " "compiled using" << end1 << "OpenCL 1.2 failed (as expected.)" << end1 << end1; } //7. , OpenCL 2.0, local_size NULL. // Blur the image with a NULL local range using the OpenCL 2.0 // compiled kernel. cout << "Compiled with OpenCL 2.0 and using a NULL local size:" << end1 << end1; output = RunBlurKernel(context, queue, kernel_2_0, global_size, cl::NullRange, input, true); //8. , OpenCL 2.0, local_size 16x16. // Blur the image with an even local range using the OpenCL 2.0 // compiled kernel. This will only work on an OpenCL 2.0 device // and compiler. cout << "Compiled with OpenCL 2.0 and using an even local size:" << end1 << end1; output = RunBlurKernel(context, queue, kernel_2_0, global_size, cl::NDRange(16, 16), input, true); //9. , . 2—5. For each option in paragraphs. 5-8, the results of a call to get_local_size () and get_get_enqueued_local_size () in each of the four corners of the NDRange are displayed on the screen. Thus, we see how the NDRange is divided into working groups. The kernel that implements the blur algorithm is stored in BoxBlur.cl. It contains a very simple implementation, but is not the most effective way to apply blur.
To build and run this training program, you need a PC that meets the following requirements:
- Intel® Core ™ processor series, codenamed Broadwell.
- Microsoft Windows * 8 or 8.1.
- Intel® SDK for OpenCL ™ applications version 2014 R2 or later.
- Microsoft Visual Studio * 2012 or later.
The training program is a console application that reads an input bitmap image and writes output raster images for each of the varieties of NDRange described in the section above. This training program supports several command line parameters: -h, -? (display of help text and output), -i <input prefix> (prefix of input bitmap image), -o <output prefix> (prefix of output bitmap image).
After starting the training program for the provided picture, the result will be as follows.
Hidden text
Input file: input.bmp Output files: output_0.bmp, output_1.bmp, output_2.bmp, output_3.bmp Device: Intel(R) HD Graphics 5500 Vendor: Intel(R) Corporation Compiled with OpenCL 1.2 and using a NULL local size: Work Item get_global_id() get_local_size() get_enqueued_local_size() ------------------------------------------------------------------------- Top left (0,0) (1,239) undefined Top right (637,0) (1,239) undefined Bottom left (0,477) (1,239) undefined Bottom right (637,477) (1,239) undefined Compiled with OpenCL 1.2 and using an even local size: Trying to launch a non-uniform workgroup with a kernel compiled using OpenCL 1.2 failed (as expected.) Compiled with OpenCL 2.0 and using a NULL local size: Work Item get_global_id() get_local_size() get_enqueued_local_size() Top left (0,0) (1,239) (1,239) Top right (637, 0) (1,239) (1,239) Bottom left (0,477) (1,239) (1,239) Bottom right (637,477) (1,239) (1,239) Compiled with OpenCL 2.0 and using an even local size: Work Item get_global_id() get_local_size() get_enqueued_local_size() Top left (0,0) (16,16) (16,16) Top right (637,0) (14,16) (16,16) Bottom left (0,477) (16,14) (16,16) Bottom right (637,477) (14,14) (16,16) Done! The input image has a size of 640x480, so the size of the NDRange in each case will be 638x478. The result above shows that running the OpenCL 1.2 kernel with the local_size parameter NULL forces you to use odd sizes for each workgroup (1, 239). Working group sizes that are not powers of two can work very slowly in some cores. SIMD conveyors may be idle, synchronous memory access may be impaired.
Running the OpenCL 1.2 kernel with the specified workgroup size (16x16) gives an error, since neither 648 nor 478 are completely divided by 16.
Running the OpenCL 2.0 kernel with the local_size parameter NULL value allows the OpenCL module to split the NDRange into workgroups of any size. The above is the result: it can be seen that the executable module continues to use the uniform size of the working groups in the same way as for the OpenCL 1.2 core.
Running an OpenCL 2.0 kernel with a given workgroup size (16x16) will result in the NDRange size being divided into heterogeneous workgroups. We see that the left upper working group has a size of 16x16, the upper right is 14x16, the lower left is 16x14, and the lower right is 14x14. Since in most cases the size of the working group is 16x16, this core will use SIMD pipelines very efficiently and memory access will be very fast.
Full versions of articles on the IDZ website:
Original articles in English:
Source: https://habr.com/ru/post/246091/
All Articles