Maximum XOR
Hello, Habr. And immediately to the point.
Task:
There are two integers: L and R. It is necessary to find the maximum value of A xor B on the interval [L; R] , where L ≤ A ≤ B ≤ R.
It would seem nothing complicated. Immediately begs the decision by simple brute force.
And what if there are 1,000,000 numbers in the range. Take L = 1, and R = 1000001. How long will the average computer take to calculate the maximum value of xor on this interval? My laptop took 1699914 milliseconds.
There is a solution that works much faster, it is about him that will be discussed in this article.

In order for the resulting number to be the largest, you need to get one from the function xor in the highest possible bit of this number. And so on, in the direction of the youngest bat. In other words, we will consistently work with each bit of the resulting number in the direction from the high bits to the low bits. For this, it is very convenient to use a data structure called a trie-tree ( I like the way this data structure is described in R. Sagewick's book "Algorithms in Java" ).
Trie-trees are data structures that consist of nodes that contain references — either null, or references to other nodes. Only one other node points to each node (no node points to the root node). Each node contains R references, where R is the size of the alphabet (in our case, R = 2, since the alphabet is 0 and 1). As a rule, trie-trees contain a significant number of zero references, so they will be omitted from the pictures. Each link corresponds to the next bit of the number. Each integer is encoded as a path from the root to the leaf.
')
An example of an empty trie-tree.

This is how a trie-tree looks after adding 0, 1, 2, 3, 4, 5, 6, 7.
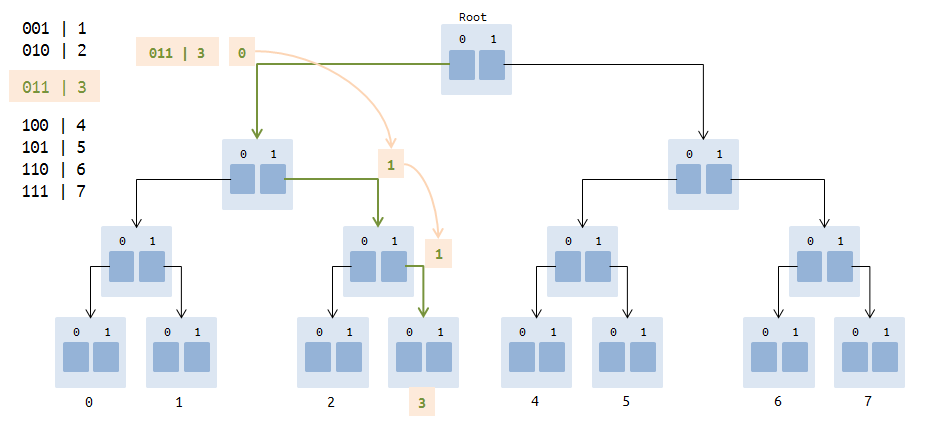
In the figure, the path consisting of 3 references is highlighted - 0 -> 1-> 1 (011 is the binary representation of the number 3).
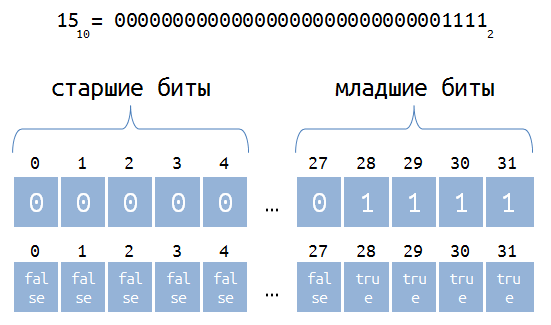
I just want to clarify that we will work only with 32-bit numbers, and the high-order bits will be filled with zeros if necessary. With this we achieve that the numbers will be stored in arrays with the same length. I decided to store the binary representation of integers in an array of type bool.
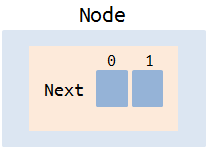
Each node stores an array of links to other nodes in the tree (2 links, one for each possible value of a bit number).
In general, a trie-tree is a data structure built from characters of string keys that allows you to use characters from the search key to control the search. String keys can be of different lengths; therefore, each node of the tree additionally stores a value, which can be a zero or real value associated with one of the string keys. In our case, we don’t have to store the value, since the keys are whole 32-bit numbers stored in binary form in arrays of the same length. So, trie-tree:
First, we need the functions of converting numbers from decimal to binary and vice versa. It's all very clear and simple. If you need to refresh your memory, you can peep.
Secondly, we need the function of adding an integer to a trie-tree. Here we will stop in more detail. To insert into a trie-tree, you first need to search for the desired node. The search starts with the root, and then follows the link associated with the zero (most significant) bit of the number; from this node follows the link associated with the first bit of the number; from there - by the link associated with the second bit of the number; etc., that is, you just need to view the nodes along the path from the root to some node in the trie-tree. The number bits are used to descend the tree until the last bit or zero reference is reached. If a zero reference is found before sampling the last bit of a number, i.e. in the trie-tree there is no node corresponding to the last bit of the number, it is necessary to create nodes for each of the missing bits.
Now we will build a trie-tree, adding all the numbers from the given interval.
Update: As freopen has rightly noticed,
Significant simplification of the code, but the complexity remains the same! The archive with the updated project solution can be downloaded here .
Now, we can compare the time of each of the approaches for intervals of different lengths.

As can be seen from the table, the calculation of the maximum value of xor using a trie-tree works much faster. Estimate of the complexity of the algorithm O (nlogn).
PS To solve this problem, and in general for storing integers in binary form, you can slightly simplify our trie-tree. Since the alphabet consists of only 2 characters, you can get rid of the array and store just two links, for example Node left and Node right , which are representations of 0 and 1, respectively.
Task:
There are two integers: L and R. It is necessary to find the maximum value of A xor B on the interval [L; R] , where L ≤ A ≤ B ≤ R.
It would seem nothing complicated. Immediately begs the decision by simple brute force.
Expand
The complexity of this solution is O (n 2 ).public int BruteForce(int one, int two) { int maxXor = 0; while (one < two) { int oneTemp = one + 1; while (oneTemp <= two) { int curXor = one ^ oneTemp; if (maxXor < curXor) maxXor = curXor; oneTemp++; } one++; } return maxXor; } And what if there are 1,000,000 numbers in the range. Take L = 1, and R = 1000001. How long will the average computer take to calculate the maximum value of xor on this interval? My laptop took 1699914 milliseconds.
There is a solution that works much faster, it is about him that will be discussed in this article.

Main idea.
In order for the resulting number to be the largest, you need to get one from the function xor in the highest possible bit of this number. And so on, in the direction of the youngest bat. In other words, we will consistently work with each bit of the resulting number in the direction from the high bits to the low bits. For this, it is very convenient to use a data structure called a trie-tree ( I like the way this data structure is described in R. Sagewick's book "Algorithms in Java" ).
Trie-trees are data structures that consist of nodes that contain references — either null, or references to other nodes. Only one other node points to each node (no node points to the root node). Each node contains R references, where R is the size of the alphabet (in our case, R = 2, since the alphabet is 0 and 1). As a rule, trie-trees contain a significant number of zero references, so they will be omitted from the pictures. Each link corresponds to the next bit of the number. Each integer is encoded as a path from the root to the leaf.
')
An example of an empty trie-tree.

This is how a trie-tree looks after adding 0, 1, 2, 3, 4, 5, 6, 7.

In the figure, the path consisting of 3 references is highlighted - 0 -> 1-> 1 (011 is the binary representation of the number 3).
I just want to clarify that we will work only with 32-bit numbers, and the high-order bits will be filled with zeros if necessary. With this we achieve that the numbers will be stored in arrays with the same length. I decided to store the binary representation of integers in an array of type bool.

Each node stores an array of links to other nodes in the tree (2 links, one for each possible value of a bit number).

In general, a trie-tree is a data structure built from characters of string keys that allows you to use characters from the search key to control the search. String keys can be of different lengths; therefore, each node of the tree additionally stores a value, which can be a zero or real value associated with one of the string keys. In our case, we don’t have to store the value, since the keys are whole 32-bit numbers stored in binary form in arrays of the same length. So, trie-tree:
using System; namespace MaxXor { public class Trie { //for integer representation in binary system 2^32 public static readonly int MaxLengthOfBits = 32; //size of alphabet public static readonly int N = 2; class Node { public Node[] next = new Node[Trie.N]; } private Node _root; } } First, we need the functions of converting numbers from decimal to binary and vice versa. It's all very clear and simple. If you need to refresh your memory, you can peep.
ConvertDecimalToBInary
private bool[] ConvertDecimalToBInary(int number) { int counter = Trie.MaxLengthOfBits; bool[] result = new bool[counter]; while (number > 0) { result[--counter] = Convert.ToBoolean(number % 2); number /= 2; } return result; } ConvertBinaryToDecimal
private int ConvertBinaryToDecimal(bool[] bits) { int result = 0; int base_val = 1; for (int i = bits.Length - 1; i >= 0; i--) { result += Convert.ToInt32(bits[i]) * base_val; base_val *= 2; } return result; } Secondly, we need the function of adding an integer to a trie-tree. Here we will stop in more detail. To insert into a trie-tree, you first need to search for the desired node. The search starts with the root, and then follows the link associated with the zero (most significant) bit of the number; from this node follows the link associated with the first bit of the number; from there - by the link associated with the second bit of the number; etc., that is, you just need to view the nodes along the path from the root to some node in the trie-tree. The number bits are used to descend the tree until the last bit or zero reference is reached. If a zero reference is found before sampling the last bit of a number, i.e. in the trie-tree there is no node corresponding to the last bit of the number, it is necessary to create nodes for each of the missing bits.
public void AddValue(bool[] binaryNumber) { _root = AddValue(_root, binaryNumber, 0); } private Node AddValue(Node node, bool[] val, int d) { if (node == null) node = new Node(); //if least sagnificient bit has been added //need return if (d == val.Length) { return node; } // get 0 or 1 index of next array(length 2) int index = Convert.ToInt32(val[d]); node.next[index] = AddValue(node.next[index], val, ++d); return node; } Now we will build a trie-tree, adding all the numbers from the given interval.
Update: As freopen has rightly noticed,
it is enough to find the very first bit, which is different, nothing can be done with the bits above;So, we find the very first bit, which is different, for this we will move from the root of the links until we meet a node that has both links. Then all the bits below are made in units. As a result, we get the result.
public bool[] GetMaxXor() { bool[] result = new bool[Trie.MaxLengthOfBits]; Node cur = _root; //find index the most significant bit, which is different int index; for (index = 0; index < Trie.MaxLengthOfBits; index++) { //are bits differ? if (cur.next[0] != null && cur.next[1] != null) { //the most significant bit, which is different result[index] = true; break; } //descent down the tree cur = cur.next[0] ?? cur.next[1]; } //all the bits below do 1 while (index < Trie.MaxLengthOfBits) { result[index] = true; index++; } return result; } Significant simplification of the code, but the complexity remains the same! The archive with the updated project solution can be downloaded here .
Old version
We turn to the most important thing. To find the maximum value of xor, we will move along the trie-tree from the root of the links, that is, we will work with bits in the direction from older to younger ones. And we can be both in one node, and in different. During each pass, we will try to get a unit, if possible, from the xor of the next bits of numbers, and so on, until we get all 32 bits. The resulting 32 bits - this is the maximum value of xor in our gap.
Example for 3-bit numbers

The archive with the project solution can be downloaded here .
We turn to the most important thing. To find the maximum value of xor, we will move along the trie-tree from the root of the links, that is, we will work with bits in the direction from older to younger ones. And we can be both in one node, and in different. During each pass, we will try to get a unit, if possible, from the xor of the next bits of numbers, and so on, until we get all 32 bits. The resulting 32 bits - this is the maximum value of xor in our gap.
public bool[] GetMaxXor() { bool[] result = new bool[Trie.MaxLengthOfBits]; Node oneNode = _root, twoNode = _root; //for each bit from most significant bit to least significant bit for (int i = 0; i < Trie.MaxLengthOfBits; i++) { //getting current bit result[i] = GetBit(oneNode, twoNode); //go to next nodes UpdateNodes(ref oneNode, ref twoNode); } return result; } //we need update nodes after each iteration //we can stay on single node or split on two nodes private void UpdateNodes(ref Node one, ref Node two) { if (one.Equals(two)) { if (one.next[1] != null && one.next[0] != null) { two = one.next[1]; one = one.next[0]; } else { one = two = ((one.next[1] != null) ? one.next[1] : one.next[0]); } } else { if (one.next[1] != null && two.next[0] != null) { one = one.next[1]; two = two.next[0]; } else if (one.next[0] != null && one.next[1] == null) { one = one.next[0]; two = two.next[1]; } else { one = one.next[1] ?? one.next[0]; two = two.next[1] ?? two.next[0]; } } } //if it's possible, we will try to get one. private bool GetBit(Node one, Node two) { if (one.Equals(two)) { // 0 xor 1 == 1; 1 xor 0 == 1 if (one.next[0] != null && one.next[1] != null) return true; // 0 xor 0 == 0; 1 xor 1 == 0 else return false; } else { if ((one.next[1] != null && two.next[0] != null) || // 1 xor 0 == 1 (one.next[0] != null && one.next[1] == null)) // 0 xor 1 == 1 { return true; } else {// 0 xor 0 == 0; 1 xor 1 == 0 return false; } } } Example for 3-bit numbers

The archive with the project solution can be downloaded here .
Now, we can compare the time of each of the approaches for intervals of different lengths.

As can be seen from the table, the calculation of the maximum value of xor using a trie-tree works much faster. Estimate of the complexity of the algorithm O (nlogn).
PS To solve this problem, and in general for storing integers in binary form, you can slightly simplify our trie-tree. Since the alphabet consists of only 2 characters, you can get rid of the array and store just two links, for example Node left and Node right , which are representations of 0 and 1, respectively.
Source: https://habr.com/ru/post/245801/
All Articles