Algorithm TILT or non-standard use of the rank of the matrix
Today we will look at the TILT (Transform Invariant Low-rank Texture) algorithm and many of its methods of application in the field of Computer Vision. The article will carry a few overview, without a deep deepening in the math of the math.
The idea of the algorithm, one might say, comes from the competition Netflix Prize , which, in fact, is the task of collaborative filtering, where we have a matrix of users and their ratings: the matrix is sparse, there are no elements in it, and there may also be noise, but we need to for each movie to predict what assessment each user will give him, i.e. we fill the matrix.
The image is also a matrix!
We will use the definition of the rank of the matrix

')
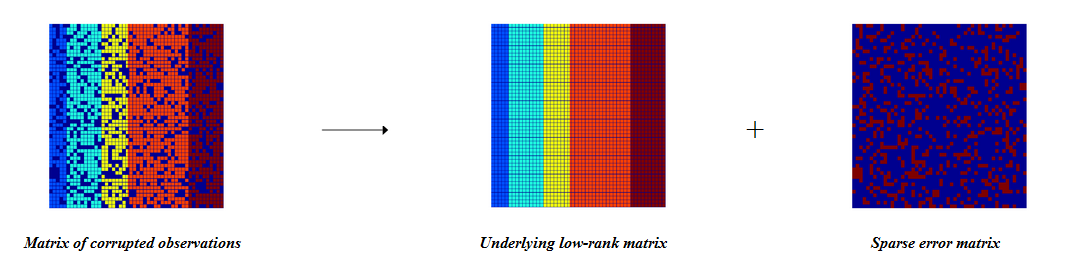
As shown in the picture above the post, we model our original matrix as a low-rank matrix (low rank) + sparse matrix with noise, i.e. in fact, it might look something like this:

Now about the TILT algorithm itself:
To the original formulation of the problem, we add distortion, i.e. we recover not only the low rank matrix and the noise matrix, but also geometric distortion (for example, rotation, affine transformation, projective transformation) at which the rank of the matrix is minimized.
We will define our transformation by the homography matrix, although it is possible to define a more complex transformation.
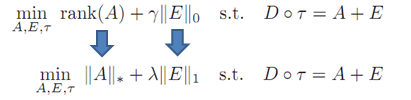
But in practice, the rank of the matrix is not minimized directly, but nuclear norm is taken, and for the matrix with noise, L1 norm is taken, as I understand it is done for regularization, i.e. so that the matrix is sparse.
Setting the minimization problem:
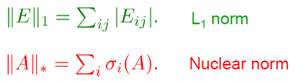
Then the algorithm iteratively converges to the optimal solution using optimization methods, as shown in the video:
A small bonus example: reduction of the matrix dimension via SVD:
An image with a regular structure is taken and a rectangular hole is made in it (the color of the pixels is equal to 0)
rank 5

rank 15

rank 100

Now we turn to the most interesting, namely to practical applications:
Auto-distortion lens:

Augmented Reality:

Auto-rotate text, signage and barcode:


And yes, not only pictures with a repeating structure have a low rank, but also symmetry lowers the rank! It is also worth noting that if a person has a bandage on one eye (pirate person) or a bang on one side, this will not interfere with the “find symmetry” algorithm, because we remember that the algorithm also models noise.
Auto-rotate people, goats and any items with symmetry:

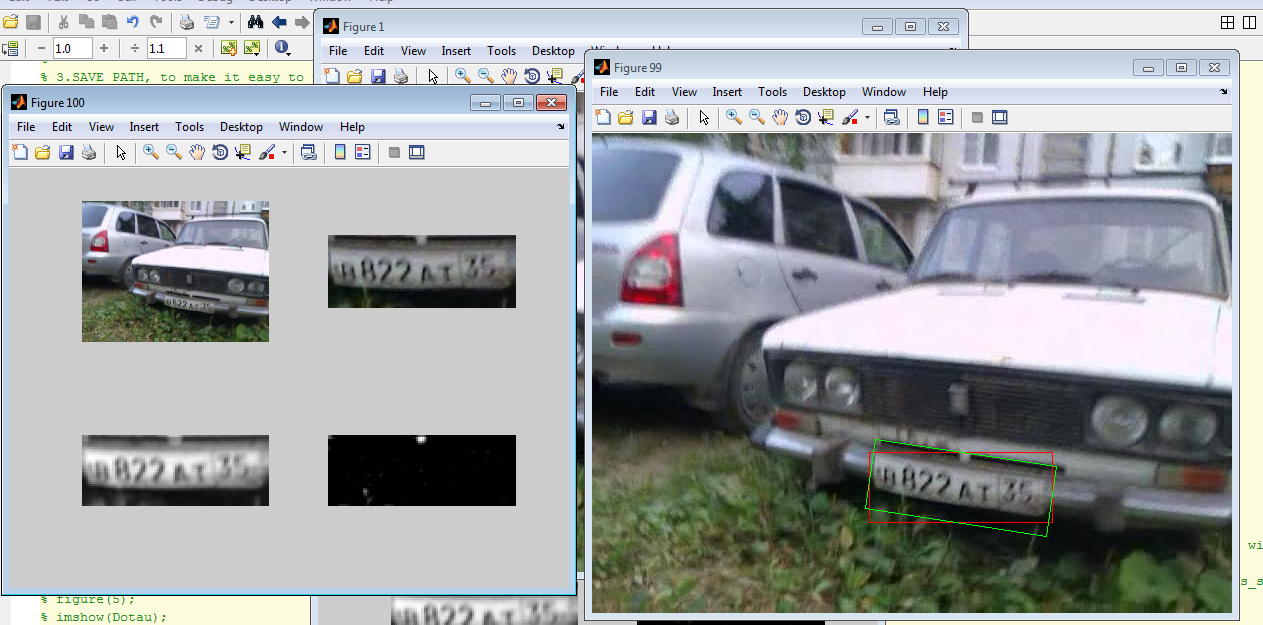
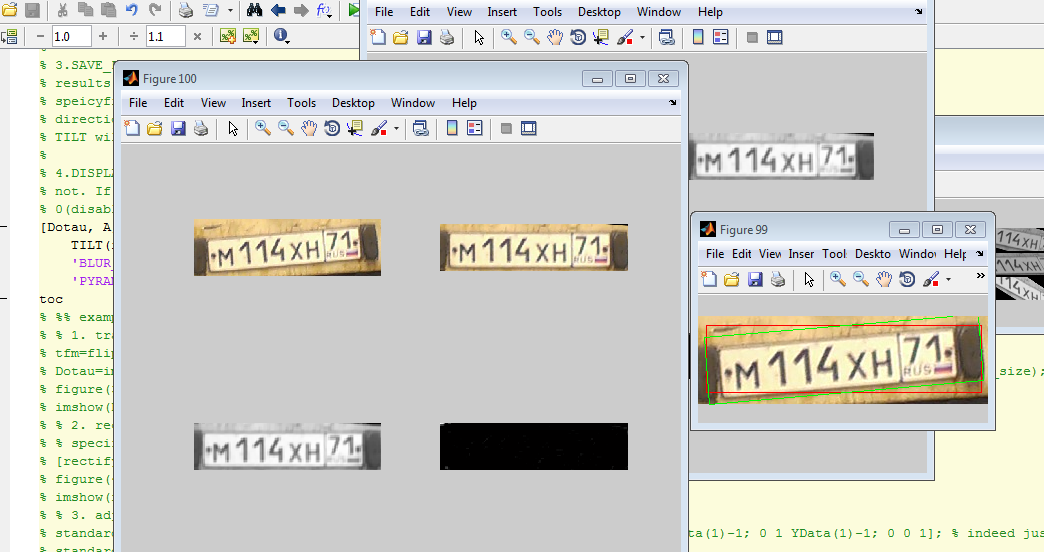
Auto-rotate the license plate number (a small hello to recent posts about recognizing the license plate number from ZlodeiBaal images taken from here ):
Another area in which this algorithm can be used is the Inpainting task, but the benefits are dubious, because a regular structure is required and the details will be removed.

Is the algorithm really so good ?
Not really. The convergence of the algorithm to the correct solution depends on the initialization, here are a couple of negative examples:

What's next?
Link to the original Matlab code: TILT code
Link to C ++ code from Smorodov : TILT-Cpp-port and SelfCalibration
Publication links: TILT: Transform Invariant Low-rank Textures
Links to lectures: Low-rank modeling | Yi Ma, Microsoft, The Pursuit of Low-Dimensional Structures
The idea of the algorithm, one might say, comes from the competition Netflix Prize , which, in fact, is the task of collaborative filtering, where we have a matrix of users and their ratings: the matrix is sparse, there are no elements in it, and there may also be noise, but we need to for each movie to predict what assessment each user will give him, i.e. we fill the matrix.
The image is also a matrix!
We will use the definition of the rank of the matrix
The rank of the system of rows (columns) of a matrix A with m rows and n columns is the maximum number of linearly independent rows (columns). Several rows (columns) are called linearly independent if none of them is expressed linearly through the others. The rank of the row system is always equal to the rank of the column system, and this number is called the rank of the matrix.And what image will have a low rank? For example, an image where there are regular structures:
')
As shown in the picture above the post, we model our original matrix as a low-rank matrix (low rank) + sparse matrix with noise, i.e. in fact, it might look something like this:
Now about the TILT algorithm itself:
To the original formulation of the problem, we add distortion, i.e. we recover not only the low rank matrix and the noise matrix, but also geometric distortion (for example, rotation, affine transformation, projective transformation) at which the rank of the matrix is minimized.
We will define our transformation by the homography matrix, although it is possible to define a more complex transformation.
But in practice, the rank of the matrix is not minimized directly, but nuclear norm is taken, and for the matrix with noise, L1 norm is taken, as I understand it is done for regularization, i.e. so that the matrix is sparse.
Setting the minimization problem:
Then the algorithm iteratively converges to the optimal solution using optimization methods, as shown in the video:
A small bonus example: reduction of the matrix dimension via SVD:
An image with a regular structure is taken and a rectangular hole is made in it (the color of the pixels is equal to 0)
rank 5

rank 15

rank 100

Code
clc clear
k = 100; % rank
% A is the mxn matrix we want to decompose
A = im2double (rgb2gray (imread ('low_rank_img.jpg'))) ';
sz = size (A)
% make black hole
A (100: 100 + sz (1) / 8,100: 100 + sz (2) / 10) = 0;
kmax = min (size (A));
if (k> kmax)
k = kmax;
end
tic
% Compute SVD of A directly
[u0, S0, V0] = svd (A, 'econ');
A0 = U0 (:, 1: k) * S0 (1: k, 1: k) * V0 (:, 1: k) ';
rank (A0)% test if rank = k
toc
display (['SVD Error:' num2str (norm (A (:) - A0 (:)) / norm (A (:)))])
clear U0 S0 V0
k = 100; % rank
% A is the mxn matrix we want to decompose
A = im2double (rgb2gray (imread ('low_rank_img.jpg'))) ';
sz = size (A)
% make black hole
A (100: 100 + sz (1) / 8,100: 100 + sz (2) / 10) = 0;
kmax = min (size (A));
if (k> kmax)
k = kmax;
end
tic
% Compute SVD of A directly
[u0, S0, V0] = svd (A, 'econ');
A0 = U0 (:, 1: k) * S0 (1: k, 1: k) * V0 (:, 1: k) ';
rank (A0)% test if rank = k
toc
display (['SVD Error:' num2str (norm (A (:) - A0 (:)) / norm (A (:)))])
clear U0 S0 V0
Now we turn to the most interesting, namely to practical applications:
Auto-distortion lens:
Augmented Reality:
Auto-rotate text, signage and barcode:
And yes, not only pictures with a repeating structure have a low rank, but also symmetry lowers the rank! It is also worth noting that if a person has a bandage on one eye (pirate person) or a bang on one side, this will not interfere with the “find symmetry” algorithm, because we remember that the algorithm also models noise.
Auto-rotate people, goats and any items with symmetry:
Auto-rotate the license plate number (a small hello to recent posts about recognizing the license plate number from ZlodeiBaal images taken from here ):
Another area in which this algorithm can be used is the Inpainting task, but the benefits are dubious, because a regular structure is required and the details will be removed.
Is the algorithm really so good ?
Not really. The convergence of the algorithm to the correct solution depends on the initialization, here are a couple of negative examples:
What's next?
Link to the original Matlab code: TILT code
Link to C ++ code from Smorodov : TILT-Cpp-port and SelfCalibration
Publication links: TILT: Transform Invariant Low-rank Textures
Links to lectures: Low-rank modeling | Yi Ma, Microsoft, The Pursuit of Low-Dimensional Structures
Source: https://habr.com/ru/post/245497/
All Articles