Hacker's guide to neural networks. Schemes of real values. Schemes with several logical elements
Content:
You will probably say: “The analytical gradient is quite simple, if you take the derivative for your simple expressions. But it is useless. What will I do when expressions get much bigger? Wouldn't the equations get huge and complex pretty quickly? ” Good question. Yes, expressions are becoming much more complicated. But no, it does not make everything much more difficult.
As we will see later, each logical element will exist by itself, completely unaware of the nuances of a huge and complex scheme, of which it is a part. He will only worry about his original values, and will calculate his local derivatives in the same way as described in the previous section, except that there will be one additional multiplication that he will need to perform.
')
Probably stop praising him. I hope I aroused your interest. Let's delve into the details and include two logical elements in our next example:
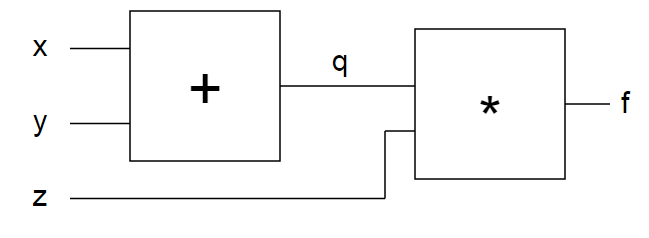
The expression we are calculating at the moment looks like this: f (x, y, z) = (x + y) z . Let's build the code structure to represent the logic elements as functions:
In the above example, I use a and b as local variables in the functions of the logic elements. Thus, we will not confuse them with the initial values of the x, y, z scheme. As before, we are interested in finding derivatives with respect to these three initial values: x, y, z . But how are we going to count them now, when we have several logical elements?
To begin with, let's pretend that the + element is not here, and that we have only two variables in the scheme: q, z and one logical element *. Notice that q is the resulting value of the logical element +. If we do not need to worry about x and y, but only about q and z, then we return to only one logical element, since only the element * is involved, and we know what the (analytical) derivatives of the previous section are. We can write them (in this case, replacing x, y with q, z) as follows:
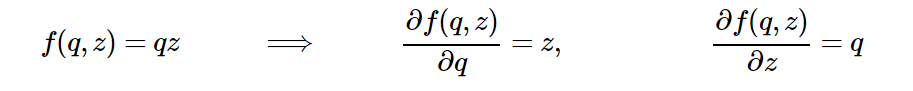
Everything is quite simple: these are gradient expressions with respect to q and z. But wait, we do not need a gradient with respect to q, but only with respect to the initial values: x and y. Fortunately, q is calculated as a function of x and y (by adding in our example). We can write the gradient for the addition logic in the same way, even simpler:
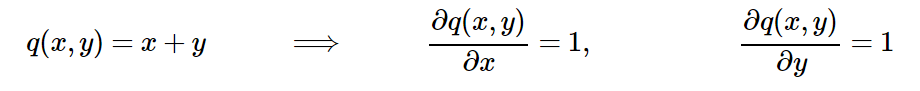
Everything is correct, the derivatives are simply equal to 1, regardless of the actual x and y values. If you think about it, then it makes sense, because to make the result of one logical element of addition higher, we need a positive change of x and y, regardless of their values.
Back propagation error
Finally, we are ready to use the Chain rule: we know how to calculate the q gradient with respect to x and y (this is in the case of one logical element - +). And we know how to calculate the gradient of our final result with respect to q. The chain rule tells us how to combine these approaches to get the final result gradient with respect to x and y, which we are ultimately interested in. Best of all, the chain rule simply states that the right thing is to take and multiply the gradients to link them. For example, the final derivative for x would be:
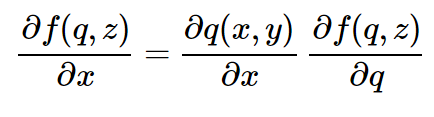
There are a lot of characters, so again, this may seem complicated, but these are just two numbers that are multiplied together. Here is the code:
That's all. We calculated the gradient and now we can allow our original values to react a bit to it. Let's add gradients to the top of the original values. The output value of the circuit needs to be done more than -12!
Seems to work! Let's now try to intuitively interpret what has just happened. The circuit wants to produce higher values as a result. The last logical element saw the initial values q = 3, z = -4 and calculated the result -12. By “pushing” up, this output value applied a force on both q and z : to increase the output value, the “wants” circuit would increase the value of z , as can be seen from the positive value of the derivative (derivative_f_wrt_z = +3) . Again, the size of this derivative can be interpreted as the magnitude of the force. On the one hand, a large downward force was applied to q, since the derivative_f_wrt_q = -4 . In other words, the scheme wants to reduce q by applying a force equal to 4 to it.
Now we come to the second logical element - "+" , which gives the output value q . By default, the logical element + calculates its derivatives, which tell us how to change x and y to make q larger. BUT! Here is an important point : the gradient of the q value was calculated as a negative number ( derivative_f_wrt_q = -4 ), so the circuit wants to reduce the q module by applying a force equal to 4! Therefore, if the logical element + wants to help make the final output value larger, it must listen to the gradient signals coming from above. In particular, in this case, he should push x, y in the opposite direction from where he could push them under normal conditions, and with a force equal to 4, so to speak. Multiplication by -4, used in the chain rule, leads to the following: instead of applying a positive force of +1 on both x and y (local derivative), the total gradient of the circuit in x and y becomes 1 x -4 = -4 . This makes sense: the circuit wants x and y to become smaller, since this will lead to a decrease in q, which, in turn, will increase f.
Let's repeat what we learned:
In the previous section, we saw that in the case of one logical element (or one expression), we can take the derivative of an analytical gradient using a simple calculation. We interpreted the gradient as a force or a push to the original values, which pushes them in a direction that can make the result of this logical element higher.
In the case of several logical elements, everything remains approximately the same: each logical element exists independently, unaware of the scheme in which it is included. Some source values arrive, and the logical element calculates the result and the derivative with respect to the source values. The only difference at this stage is that suddenly something can push this logical element from above. This is the gradient of the final output value of the circuit in relation to the result that this logical element calculated. It is the circuit that asks the logical element to result in a larger or smaller number, applying a certain force. The logical element simply takes this force and multiplies it by all the forces that it has calculated before for its initial values (chain rule). This led to the desired results:
1. If a logical positive impulse from above turns out to be a logical element, it also pushes its own initial values, differentiated by the force applied to it from above
2. And if there is a negative push on it, it means that the circuit wants its value to decrease, not increase, so it will apply push force to its original values in order to make its own output value smaller.
Isn't that great? The only difference between a scenario with one logical element and several interacting logical elements that arbitrarily compute complex expressions is the additional multiplication that occurs in each logical element.
You will probably say: “The analytical gradient is quite simple, if you take the derivative for your simple expressions. But it is useless. What will I do when expressions get much bigger? Wouldn't the equations get huge and complex pretty quickly? ” Good question. Yes, expressions are becoming much more complicated. But no, it does not make everything much more difficult.
As we will see later, each logical element will exist by itself, completely unaware of the nuances of a huge and complex scheme, of which it is a part. He will only worry about his original values, and will calculate his local derivatives in the same way as described in the previous section, except that there will be one additional multiplication that he will need to perform.
One additional multiplication will transform one (useless) logic element into a gear in a complex mechanism, which is a whole neural network.
')
Probably stop praising him. I hope I aroused your interest. Let's delve into the details and include two logical elements in our next example:
The expression we are calculating at the moment looks like this: f (x, y, z) = (x + y) z . Let's build the code structure to represent the logic elements as functions:
var forwardMultiplyGate = function(a, b) { return a * b; }; var forwardAddGate = function(a, b) { return a + b; }; var forwardCircuit = function(x,y,z) { var q = forwardAddGate(x, y); var f = forwardMultiplyGate(q, z); return f; }; var x = -2, y = 5, z = -4; var f = forwardCircuit(x, y, z); // -12 In the above example, I use a and b as local variables in the functions of the logic elements. Thus, we will not confuse them with the initial values of the x, y, z scheme. As before, we are interested in finding derivatives with respect to these three initial values: x, y, z . But how are we going to count them now, when we have several logical elements?
To begin with, let's pretend that the + element is not here, and that we have only two variables in the scheme: q, z and one logical element *. Notice that q is the resulting value of the logical element +. If we do not need to worry about x and y, but only about q and z, then we return to only one logical element, since only the element * is involved, and we know what the (analytical) derivatives of the previous section are. We can write them (in this case, replacing x, y with q, z) as follows:
Everything is quite simple: these are gradient expressions with respect to q and z. But wait, we do not need a gradient with respect to q, but only with respect to the initial values: x and y. Fortunately, q is calculated as a function of x and y (by adding in our example). We can write the gradient for the addition logic in the same way, even simpler:
Everything is correct, the derivatives are simply equal to 1, regardless of the actual x and y values. If you think about it, then it makes sense, because to make the result of one logical element of addition higher, we need a positive change of x and y, regardless of their values.
Back propagation error
Finally, we are ready to use the Chain rule: we know how to calculate the q gradient with respect to x and y (this is in the case of one logical element - +). And we know how to calculate the gradient of our final result with respect to q. The chain rule tells us how to combine these approaches to get the final result gradient with respect to x and y, which we are ultimately interested in. Best of all, the chain rule simply states that the right thing is to take and multiply the gradients to link them. For example, the final derivative for x would be:
There are a lot of characters, so again, this may seem complicated, but these are just two numbers that are multiplied together. Here is the code:
// var x = -2, y = 5, z = -4; var q = forwardAddGate(x, y); // q 3 var f = forwardMultiplyGate(q, z); // -12 // // wrt – « » ("with respect to") var derivative_f_wrt_z = q; // 3 var derivative_f_wrt_q = z; // -4 // var derivative_q_wrt_x = 1.0; var derivative_q_wrt_y = 1.0; // var derivative_f_wrt_x = derivative_q_wrt_x * derivative_f_wrt_q; // -4 var derivative_f_wrt_y = derivative_q_wrt_y * derivative_f_wrt_q; // -4 That's all. We calculated the gradient and now we can allow our original values to react a bit to it. Let's add gradients to the top of the original values. The output value of the circuit needs to be done more than -12!
// , : [-4, -4, 3] var gradient_f_wrt_xyz = [derivative_f_wrt_x, derivative_f_wrt_y, derivative_f_wrt_z] // /: var step_size = 0.01; x = x + step_size * derivative_f_wrt_x; // -2.04 y = y + step_size * derivative_f_wrt_y; // 4.96 z = z + step_size * derivative_f_wrt_z; // -3.97 // : var q = forwardAddGate(x, y); // q 2.92 var f = forwardMultiplyGate(q, z); // -11.59, , -12! Seems to work! Let's now try to intuitively interpret what has just happened. The circuit wants to produce higher values as a result. The last logical element saw the initial values q = 3, z = -4 and calculated the result -12. By “pushing” up, this output value applied a force on both q and z : to increase the output value, the “wants” circuit would increase the value of z , as can be seen from the positive value of the derivative (derivative_f_wrt_z = +3) . Again, the size of this derivative can be interpreted as the magnitude of the force. On the one hand, a large downward force was applied to q, since the derivative_f_wrt_q = -4 . In other words, the scheme wants to reduce q by applying a force equal to 4 to it.
Now we come to the second logical element - "+" , which gives the output value q . By default, the logical element + calculates its derivatives, which tell us how to change x and y to make q larger. BUT! Here is an important point : the gradient of the q value was calculated as a negative number ( derivative_f_wrt_q = -4 ), so the circuit wants to reduce the q module by applying a force equal to 4! Therefore, if the logical element + wants to help make the final output value larger, it must listen to the gradient signals coming from above. In particular, in this case, he should push x, y in the opposite direction from where he could push them under normal conditions, and with a force equal to 4, so to speak. Multiplication by -4, used in the chain rule, leads to the following: instead of applying a positive force of +1 on both x and y (local derivative), the total gradient of the circuit in x and y becomes 1 x -4 = -4 . This makes sense: the circuit wants x and y to become smaller, since this will lead to a decrease in q, which, in turn, will increase f.
If this makes sense to you, then you understand the reverse propagation of an error.
Let's repeat what we learned:
In the previous section, we saw that in the case of one logical element (or one expression), we can take the derivative of an analytical gradient using a simple calculation. We interpreted the gradient as a force or a push to the original values, which pushes them in a direction that can make the result of this logical element higher.
In the case of several logical elements, everything remains approximately the same: each logical element exists independently, unaware of the scheme in which it is included. Some source values arrive, and the logical element calculates the result and the derivative with respect to the source values. The only difference at this stage is that suddenly something can push this logical element from above. This is the gradient of the final output value of the circuit in relation to the result that this logical element calculated. It is the circuit that asks the logical element to result in a larger or smaller number, applying a certain force. The logical element simply takes this force and multiplies it by all the forces that it has calculated before for its initial values (chain rule). This led to the desired results:
1. If a logical positive impulse from above turns out to be a logical element, it also pushes its own initial values, differentiated by the force applied to it from above
2. And if there is a negative push on it, it means that the circuit wants its value to decrease, not increase, so it will apply push force to its original values in order to make its own output value smaller.
A good example to keep in mind: we push the result of the circuit and this leads to a downward push through the whole circuit down to the original values.
Isn't that great? The only difference between a scenario with one logical element and several interacting logical elements that arbitrarily compute complex expressions is the additional multiplication that occurs in each logical element.
Source: https://habr.com/ru/post/245403/
All Articles