Hacker's guide to neural networks. Schemes of real values. Strategy # 3: Analytical Gradient
Content:
In the previous section, we estimated the gradient by examining the output value of the circuit for each initial value separately. This procedure gives us what we call the numerical gradient. However, this approach is still considered quite problematic, since we need to calculate the result of the circuit as each initial value changes by a small number. Therefore, the complexity of the gradient estimate is linear in the number of initial values. But in practice we will have hundreds, thousands or (for neural networks) from tens to hundreds of millions of initial values, and the schemes will include not only one logical element of multiplication, but also huge expressions that can be very difficult to calculate. We need something better.
Fortunately, there is a simpler and much faster way to calculate the gradient: we can use the calculation method for the derivative of a direct expression, which will be as easy to estimate as the output value of the circuit. We call it an analytical gradient, and there’s no need to substitute something here. You must have seen how other people who train neural networks take gradient derivatives using huge and, even speaking, scary and complex mathematical equations (if you are not very strong in mathematics). But this is optional. I wrote a huge amount of code for neural networks and I rarely have to take mathematical derivatives longer than two lines, and in 95% of cases this can be done without having to write anything at all. This is all because we are unlikely to take the derivative of the gradient for very small and simple expressions (consider this as a base case), and then I will show you how you can quite easily construct such expressions with the help of a chain rule for evaluating the whole gradient (consider it inductive / recursive case).
')
If you remember the rules of the work, the rules of exponentiation, the rules of the particular (see the rules of derivatives or the Wikipedia page), you will simply write the derivative with respect to x and y for small expressions like x * y. But suppose you do not remember the rules of differential computation. We can return to the definition. For example, here’s a derivative with respect to x:

(Technically, I do not write the limit in the form of h tending to zero. Forgive me, mathematics). Good. Now let's include our function (f (x, y) = xy) in the expression. Ready for the most difficult mathematical part in this whole article? Here she is:
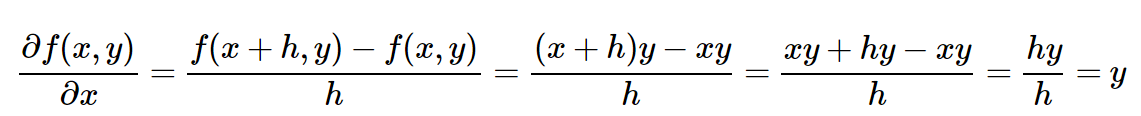
It is interesting. The derivative with respect to x is simply equal to y. Did you notice a match with the previous section? We changed x to x + h and calculated x_derivative = 3.0, which, in fact, turns out to be the value of y in this example. It turns out that this was not a coincidence as such, since this is just how, according to the analytic gradient, the derivative x should look like for f (x, y) = x * y. The derivative with respect to y, however, turns out to be equal to x, which is not surprising. Therefore, there is no need to substitute! We used the power of mathematics and now we can convert our derivative calculations into the following code:
To calculate the gradient, we went from iterating through the scheme hundreds of times ( Strategy No. 1 ) to the number of iterations twice the number of initial values ( Strategy No. 2 ), and until it was moved only once! And it becomes MORE better, since more costly strategies (# 1 and # 2) give only an approximate gradient, while # 3 (the fastest way at the moment) gives an exact gradient. No approximate values. The only downside is that you should feel confident in differential computing.
Let's briefly repeat what we have learned:
INITIAL VALUE: We are given a diagram, some initial values, and we have to calculate the output value.
OUTPUT VALUE: We are interested in finding small changes to each source value (individually) that can make the output value higher.
Strategy # 1 : One simple way, which is to randomly search for small changes in the original values and track which value leads to the greatest increase in output.
Strategy number 2 : We saw that we can more as regards the calculation of the gradient. Regardless of how complex the scheme is, the numerical gradient is fairly simple (but relatively time consuming) in the calculations. We calculate it by probing the output values of the circuit as the initial values are substituted one by one.
Strategy # 3: Ultimately, we realized that we can be smarter and analytically take the derivative of a direct expression to obtain an analytical gradient. It is similar to a numerical gradient, but at the moment is the fastest, and also does not require the substitution of values.
In practice, by the way (and we will come back to this one more time), all libraries of neural networks always calculate the analytical gradient, but the correctness of execution is checked by comparing it with a numerical gradient. This is because the numerical gradient is very simple to estimate (but it can be a little time consuming in calculating), while the analytical gradient can sometimes contain errors, but it is usually quite effective in calculating. As we will see later, the gradient estimate (i.e., in the process of performing backward propagation of an error or backward pass), turns out to have the same meaning as the forward pass estimate.
In the previous section, we estimated the gradient by examining the output value of the circuit for each initial value separately. This procedure gives us what we call the numerical gradient. However, this approach is still considered quite problematic, since we need to calculate the result of the circuit as each initial value changes by a small number. Therefore, the complexity of the gradient estimate is linear in the number of initial values. But in practice we will have hundreds, thousands or (for neural networks) from tens to hundreds of millions of initial values, and the schemes will include not only one logical element of multiplication, but also huge expressions that can be very difficult to calculate. We need something better.
Fortunately, there is a simpler and much faster way to calculate the gradient: we can use the calculation method for the derivative of a direct expression, which will be as easy to estimate as the output value of the circuit. We call it an analytical gradient, and there’s no need to substitute something here. You must have seen how other people who train neural networks take gradient derivatives using huge and, even speaking, scary and complex mathematical equations (if you are not very strong in mathematics). But this is optional. I wrote a huge amount of code for neural networks and I rarely have to take mathematical derivatives longer than two lines, and in 95% of cases this can be done without having to write anything at all. This is all because we are unlikely to take the derivative of the gradient for very small and simple expressions (consider this as a base case), and then I will show you how you can quite easily construct such expressions with the help of a chain rule for evaluating the whole gradient (consider it inductive / recursive case).
The analytical derivative does not require substitutions of the original values. This derivative can be taken with the help of mathematics (differential calculations).
')
If you remember the rules of the work, the rules of exponentiation, the rules of the particular (see the rules of derivatives or the Wikipedia page), you will simply write the derivative with respect to x and y for small expressions like x * y. But suppose you do not remember the rules of differential computation. We can return to the definition. For example, here’s a derivative with respect to x:
(Technically, I do not write the limit in the form of h tending to zero. Forgive me, mathematics). Good. Now let's include our function (f (x, y) = xy) in the expression. Ready for the most difficult mathematical part in this whole article? Here she is:
It is interesting. The derivative with respect to x is simply equal to y. Did you notice a match with the previous section? We changed x to x + h and calculated x_derivative = 3.0, which, in fact, turns out to be the value of y in this example. It turns out that this was not a coincidence as such, since this is just how, according to the analytic gradient, the derivative x should look like for f (x, y) = x * y. The derivative with respect to y, however, turns out to be equal to x, which is not surprising. Therefore, there is no need to substitute! We used the power of mathematics and now we can convert our derivative calculations into the following code:
var x = -2, y = 3; var out = forwardMultiplyGate(x, y); // : -6 var x_gradient = y; // , var y_gradient = x; var step_size = 0.01; x += step_size * x_gradient; // -2.03 y += step_size * y_gradient; // 2.98 var out_new = forwardMultiplyGate(x, y); // -5.87. ! To calculate the gradient, we went from iterating through the scheme hundreds of times ( Strategy No. 1 ) to the number of iterations twice the number of initial values ( Strategy No. 2 ), and until it was moved only once! And it becomes MORE better, since more costly strategies (# 1 and # 2) give only an approximate gradient, while # 3 (the fastest way at the moment) gives an exact gradient. No approximate values. The only downside is that you should feel confident in differential computing.
Let's briefly repeat what we have learned:
INITIAL VALUE: We are given a diagram, some initial values, and we have to calculate the output value.
OUTPUT VALUE: We are interested in finding small changes to each source value (individually) that can make the output value higher.
Strategy # 1 : One simple way, which is to randomly search for small changes in the original values and track which value leads to the greatest increase in output.
Strategy number 2 : We saw that we can more as regards the calculation of the gradient. Regardless of how complex the scheme is, the numerical gradient is fairly simple (but relatively time consuming) in the calculations. We calculate it by probing the output values of the circuit as the initial values are substituted one by one.
Strategy # 3: Ultimately, we realized that we can be smarter and analytically take the derivative of a direct expression to obtain an analytical gradient. It is similar to a numerical gradient, but at the moment is the fastest, and also does not require the substitution of values.
In practice, by the way (and we will come back to this one more time), all libraries of neural networks always calculate the analytical gradient, but the correctness of execution is checked by comparing it with a numerical gradient. This is because the numerical gradient is very simple to estimate (but it can be a little time consuming in calculating), while the analytical gradient can sometimes contain errors, but it is usually quite effective in calculating. As we will see later, the gradient estimate (i.e., in the process of performing backward propagation of an error or backward pass), turns out to have the same meaning as the forward pass estimate.
Source: https://habr.com/ru/post/245051/
All Articles