Maple: composing Lagrange equations of the 2 kind and the method of redundant coordinates

Foreword

By the nature of professional and scientific activities, I am a mechanic. I teach theoretical mechanics at the university, I write a doctoral thesis in the field of railway rolling stock dynamics. In general, this science absorbs most of my work and even free time.

With Maple (the 6th version was at the department, and the 8th was bought from the hawkers) he got acquainted with a student when he started working on a future Ph.D. under the wing of my first (now late) supervisor. There were good people who helped to figure out the package at the very first stage and start working.
')
And so gradually, most of the computational work on thesis preparation was shifted onto his shoulders. The thesis was defended, and Maple forever remained a reliable assistant in scientific work. It is often necessary to quickly evaluate a problem, set up equations, investigate them analytically, quickly obtain a numerical solution, and build graphs. In this regard, Maple is simply irreplaceable for me (in no case I want to offend the adherents of other packages).

To do everything that will be offered to the reader under the cut, I was prompted by the task brought by the student (I still have to do tutoring) from the school Olympiad. The condition of the problem is as follows:

A load hanging on a thread of length L = 1.1 m tied to a nail was pushed so that it rose, and then hit the nail. What is its speed at the moment of hitting the nail? Gravitational acceleration g = 10 m / s ² .

If you do not find fault with the necorny nebula of the condition, then the task is quite simple, and its solution, obtained by cumbersome calculations for the student, gives the result in general

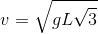
$v = \ sqrt {gL \ sqrt {3}}$

And here I wanted to check the solution obtained with an eye to the school curriculum in physics in an independent way, for example by making the differential equations of motion of this pendulum, and not simply, but taking into account the release from communication (in the process of motion, the thread considered weightless, sags and the pendulum moves as free point).

This served as a catalyst to take and dig up my old ideas accumulated from the time of work at the organizing committee of the All-Russian Olympiad of students on theoretical mechanics - for three years in a row he was engaged in the preparation of computer competition tasks. The ideas concerned the automation of the construction of equations of motion for mechanical systems with non-retaining constraints and friction, using the well-known Lagrange equations of the 2nd kind

$\ frac {d} {dt} \ left (\ frac {\ partial T} {\ partial \ dot {q} _i} \ right) - \ frac {\ partial T} {\ partial q_i} = Q_i, \ quad i = \ overline {1, s}$

Many teachers claim that the equations are not applicable to systems with non-holding bonds and friction.

As for Maple, its library for solving problems of the calculus of variations makes it possible to quickly obtain the Euler-Lagrange equations, the solution of which minimizes the Hamiltonian action, which is applicable to conservative systems

$\ frac {d} {dt} \ left (\ frac {\ partial L} {\ partial \ dot {q} _i} \ right) - \ frac {\ partial L} {\ partial q_i} = 0, \ quad i = \ overline {1, s}$

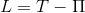Where $L = T - \ Pi$ - Lagrange function, equal to the difference between the kinetic and potential energies of the system.

Since the tasks under consideration do not belong to the conservative class, the author made an attempt to independently realize the automation of the construction and analysis of the equations of motion. What came of it is stated under the cut

1. The method of redundant coordinates

We consider a mechanical system having s degrees of freedom, whose position is described by a vector of generalized coordinates $\ vec {q} = \ left [q_1 \ left (t \ right), q_2 \ left (t \ right), ..., q_s \ left (t \ right) \ right] ^ T$ . Suppose there are also r non-holding bonds, among which reactions one can also count rest friction, when the limit value is exceeded, it transforms into an active force of sliding friction, the direction of which is opposite to the direction of the relative sliding velocity.

Accounting for non-retaining bonds requires us to determine and analyze the magnitude of their reactions, so it is also necessary to determine their magnitude. Remove these links and introduce additional r generalized coordinates, expressing through them the kinetic energy of the system

$T = T \ left (q_1, ..., q_s, q_ {s + 1}, ..., q_ {s + r}, \ dot {q} _1, ..., \ dot {q} _s, \ dot {q} _ {s + 1}, ..., \ dot {q} _ {s + r} \ right)$

We compose s + r equations of motion in the form of the Lagrange equations of the 2nd kind

$\ frac {d} {dt} \ left (\ frac {\ partial T} {\ partial \ dot {q} _i} \ right) - \ frac {\ partial T} {\ partial q_i} = Q_i, \ quad i = \ overline {1, s + r} \ quad \ quad (1)$

containing s + r unknown coordinates and r unknown bond reactions. Considering relations as retaining, we supplement this system with equations of relations (for simplicity, considering geometric relations) in the form

$f_j \ left (q_1, ..., q_ {s + r} \ right) = 0, \ quad j = \ overline {1, r}$

we obtain a closed system of equations from which the reaction values are found

$R_j = R_j \ left (q_1, ..., q_ {s}, \ dot {q} _1, ... \ dot {q} _s \ right), \ quad j = \ overline {1, r} \ quad \ quad (2)$

which are functions of the first s (independent) generalized coordinates and velocities, and they can be calculated at any step of integrating the equations of motion (1). For retention bonds of the “thread / surface” type, equations (1) and (2) must be supplemented with the condition of release from the bond

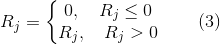
$R_j = \ left \ {\ begin {matrix} 0, \ quad R_j \ le 0 \\ R_j, \ quad R_j> 0 \ end {matrix} \ right. \ Quad \ quad (3)$

and for bonds with dry friction $F_j \ vec {\ tau} + N_j \ vec {n}$

$F_j = \ left \ {\ begin {matrix} & F_j, \ quad \ left | F_j \ right | \ le fN_j \\ & -fN_j \ cfrac {v_j} {\ left | v_j \ right |}, \ quad \ left | F_j \ right | > fN_j \ end {matrix} \ right. \ quad (4)$

where F _j and N _j respectively, the tangent and the normal component of the reaction; v _j is the projection of the relative slip rate of the reaction point.

Thus, equations (1) - (4) are a complete mathematical model of the motion of the mechanical system under consideration.

We can do away with theory and go to practice.

2. Maple-functions of construction and analysis of the Lagrange equations

To solve this problem, the lagrange Maple library was written, containing four functions

LagrangeEQs - the construction of the equations of motion in the form of Lagrange 2 kind

LagrangeEQs := proc(T, q, r, F) local s := numelems(q); local n := numelems(rk); local i, k; local T1, dT1dv; local dTdv, dTdvdt; local T2, dT2dq; local dTdq; local left_part; local Q; local summa; local r1, dr1dq, drdq; #      for i from 1 to s do #         T1[i] := subs(diff(q[i], t) = v[i], T); dT1dv[i] := diff(T1[i], v[i]); dTdv[i] := subs(v[i] = diff(q[i], t), dT1dv[i]); dTdvdt[i] := diff(dTdv[i], t); #       T2[i] := subs(q[i] = q1[i], T); dT2dq[i] := diff(T2[i], q1[i]); dTdq[i] := subs(q1[i] = q[i], dT2dq[i]); #      left_part[i] := expand(simplify(dTdvdt[i] - dTdq[i])); end do; VectorCalculus[BasisFormat](false); #    (   ) for i from 1 to s do summa := 0; for k from 1 to n do #  -   k-   i-   r1[k] := subs(q[i] = q1[i], r[k]); dr1dq[k] := VectorCalculus[diff](r1[k], q1[i]); drdq[k] := subs(q1[i] = q[i], dr1dq[k]); #        -    #    summa := summa + LinearAlgebra:-DotProduct(F[k], drdq[k], conjugate = false); end do; Q[i] := expand(simplify(summa)); end do; #      q return {seq(left_part[i] = Q[i], i=1..s)}; end proc:

As input parameters, the function accepts the expression of the kinetic energy T as a function of generalized coordinates and generalized velocities; array of generalized coordinates q ; an array of radius vectors of application points of forces r and an array of force vectors F.

LinksEQs - deriving differential constraint equations from geometric constraint equations

 LinksEQs := proc(eqs) local Eq1, Eq2; local i; local r := numelems(eqs); #       for i from 1 to r do Eq1[i] := diff(lhs(eqs[i]), t) = diff(rhs(eqs[i]), t); Eq2[i] := diff(diff(lhs(eqs[i]), t), t) = diff(diff(rhs(eqs[i]), t), t); end do; #    return {seq(eqs[i], i=1..r), seq(Eq1[i], i=1..r),seq(Eq2[i], i=1..r)}; end proc:

Here it should be noted that the system of equations of geometric relations eqs must contain redundant coordinates explicitly, that is, have the form

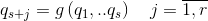
$q_ {s + j} = g \ left (q_1, .. q_s \ right) \ quad j = \ overline {1, r}$

otherwise the library functions will not be able to process the equations correctly. To test the library's capabilities, it will come down this way, but later on this point will be reworked: it is just unclear whether the system of communication equations is guaranteed to be resolved with respect to the angular redundant coordinates.

ReduceSystem - transformation of the equations of motion with regard to the equations of relations

 ReduceSystem := proc(eqs, links, q) local i, j, k; local links_eqs := LinksEQs(links); local r := numelems(links_eqs); local s := numelems(q); local eq := [seq(eqs[i], i=1..s)]; for i from 1 to s do for j from 1 to r do eq[i] := simplify(algsubs(links_eqs[j], eq[i])); end do: end do: return {seq(eq[i], i=1..s)}; end proc:

This code does not need detailed explanations - this is where the substitution of redundant generalized coordinates, velocities and accelerations, expressed by the equations of geometric and differential constraints into the equations of motion, is performed in order to bring them to a form suitable for calculating reactions of non-holding bonds

SolveAccelsReacts - solving equations of motion for reactions and generalized accelerations

 SolveAccelsReacts := proc(eqs, q, R) local s := numelems(q); local r := numelems(R); #   ,       local vars := [seq(diff(diff(q[i], t), t), i=1..s), seq(R[i], i=1..r)]; local eq := [seq(eqs[i], i=1..numelems(eqs))]; local i, j; local x; local solv; #   -  ""    for i from 1 to numelems(eqs) do for j from 1 to s + r do eq[i] := subs(vars[j] = x[j], eq[i]); end do: end do; #  "" (    ) solv := solve({seq(eq[i], i=1..numelems(eq))}, {seq(x[i], i=1..s+r)}); #      assign(solv); #  ,       return {seq(vars[i] = x[i], i=1..s+r)}; end proc:

This function takes as input a system of equations of motion eqs, transformed according to the equations of constraints. It is linear with respect to the second derivatives of independent coordinates and bond reactions. Other input parameters: q - vector of independent coordinates; R is an array of reactions for which it is necessary to solve the equations of motion.

Now we illustrate how to apply the described “farm” in

3. The problem of a pendulum on a thin inextensible thread

The design scheme will be like this. As a generalized coordinate, choose the angle 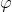$\ varphi$ tilt the filament to the vertical.

Since the thread is a non-holding bond, we will be interested in its reaction, which means we introduce an additional, redundant coordinate r ( t ).

Getting started. We clean the memory and connect the library of linear algebra

 restart; with(LinearAlgebra):

We connect lagrange library

 read `/home/maisvendoo/work/maplelibs/mechanics/lagrange.m`;

We determine the vector of generalized coordinates, calculate the coordinates and velocity of the load, as well as the kinetic energy of the system

 q := [r(t), phi(t)]; xM := q[1]*sin(q[2]); yM := -q[1]*cos(q[2]); vMx := diff(xM, t); vMy := diff(yM, t); T := simplify(m*(vMx^2 + vMy^2)/2);

At the output, we obtain an expression for the kinetic energy (for insertion, the latex () function is used here, which generates the result in LaTeX notation)
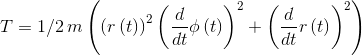
$T = 1/2 \, m \ left (\ left (r \ left (t \ right) \ right) ^ {2} \ left ({\ frac {d} {dt}} \ phi \ left (t \ right ) \ right) ^ {2} + \ left ({\ frac {d} {dt}} r \ left (t \ right) \ right) ^ {2} \ right)$

We form an array of forces and an array of coordinates of their application points

 Mg := Vector([0, -m*g]); React := Vector([-S*sin(q[2]), S*cos(q[2])]); rM := Vector([xM, yM]); Fk := [Mg, React]; rk := [rM, rM];

We feed all functions LagrangeEQs ()

 EQs := LagrangeEQs(T, q, rk, Fk):

getting output equations of motion
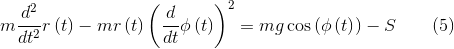
$m {\ frac {d ^ {2}} {d {t} ^ {2}}} r \ left (t \ right) -mr \ left (t \ right) \ left ({\ frac {d} {dt }} \ phi \ left (t \ right) \ right) ^ {2} = mg \ cos \ left (\ phi \ left (t \ right) \ right) -S \ quad \ quad (5)$

$2 \, mr \ left (t \ right) \ left ({\ frac {d} {dt}} \ phi \ left (t \ right) \ right) {\ frac {d} {dt}} r \ left ( t \ right) + m \ left (r \ left (t \ right) \ right) ^ {2} {\ frac {d ^ {2}} {d {t} ^ {2}}} \ phi \ left ( t \ right) = -mgr \ left (t \ right) \ sin \ left (\ phi \ left (t \ right) \ right) \ quad \ quad (6)$

It is not difficult to make sure that the function worked normally - for the illustration, a not too cumbersome task was specially chosen.

Next, we set the coupling equation - while the thread is stretched, the condition

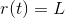
transform the system taking into account this condition and find the reaction of communication

 link_eqs := {r(t) = L}; simple_eqs := ReduceSystem(EQs, link_eqs, q); solv1 := SolveAccelsReacts(simple_eqs, [phi(t)], [S]);

The tension force of the thread is equal to
$S = m \ left ({\ frac {d} {dt}} \ phi \ left (t \ right) \ right) ^ {2} L + mg \ cos \ left (\ phi \ left (t \ right) \ right) \ quad \ quad (7)$

System (5) - (7) is a complete system of equations for the movement of the load, taking into account the possibility of thread sagging. Now we will prepare it for numerical integration. To begin with, let's solve it with respect to accelerations, passing to SolveAccelsReacts () equations (5) and (6), a vector of generalized coordinates and an empty array of reactions

 EQs2 := SolveAccelsReacts(EQs, q,[]);

getting out

${\ frac {d ^ {2}} {d {t} ^ {2}}} \ phi \ left (t \ right) = - {\ frac {2 \, \ left ({\ frac {d} {dt }} r \ left (t \ right) \ right) {\ frac {d} {dt}} \ phi \ left (t \ right) + \ sin \ left (\ phi \ left (t \ right) \ right) g} {r \ left (t \ right)}} \ quad \ quad (8)$

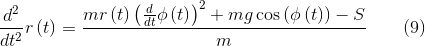
${\ frac {d ^ {2}} {d {t} ^ {2}}} r \ left (t \ right) = {\ frac {mr \ left (t \ right) \ left ({\ frac {d } {dt}} \ phi \ left (t \ right) \ right) ^ {2} + mg \ cos \ left (\ phi \ left (t \ right) \ right) -S} {m}} \ quad \ quad (9)$

For numerical simulation, although it is not sporty, we will write a separate code in order not to clog the reader’s head with a long processing of the resulting system with a file. Especially since the simulation will have its own characteristics.

We prepare the source data and the system of equations of motion

 L := 1.1: g := 10.0: #      EQs_func := proc(N, t, Y, dYdt) #     (as = S/m) local as := 0; #    ,    if Y[1] < L then as := 0; else #   ,     as := L*Y[4]^2 + g*cos(Y[2]); #    -  ,   if as < 0 then as := 0; end if; end if; #       # Y[1] -> r(t) -      # Y[2] -> phi(t) -  -    # Y[3] -> vr(t) -    # Y[4] -> omega(t) -    - dYdt[1] := Y[3]; dYdt[2] := Y[4]; dYdt[3] := Y[1]*Y[4]^2 + g*cos(Y[2]) - as; dYdt[4] := -(2*Y[3]*Y[4] + g*sin(Y[2]))/Y[1]; end proc:

We build the function of calculating the state of the system, for a given horizontal initial velocity of the load

 sys_pos := proc(v0) #    local initc := Array([L, 0, 0, v0/L]); #  ,   local q := [r(t), phi(t), vr(t), omega(t)]; #      local dsolv := dsolve(numeric, number = 4, procedure = EQs_func, start = 0, initial = initc, procvars = q, output=listprocedure); #      local R := eval(r(t), dsolv); local Phi := eval(phi(t), dsolv); local Vr := eval(vr(t), dsolv); local Omega := eval(omega(t), dsolv); return [R, Phi, Vr, Omega]; end proc:

Now we check the “school” solution of the problem.

 #     ,     v0 := evalf(sqrt(g*L*(2 + sqrt(3)))): #      eps := 1e-5: #      r := sys_pos(v0)[1]: phi := sys_pos(v0)[2]: vr := sys_pos(v0)[3]: #     x := t->r(t)*sin(phi(t)): y := t->-r(t)*cos(phi(t)): #      t1 := fsolve(r(t) = eps, t=0..10.0): #      v := vr(t1); #    plot([x(t), y(t), t=0..t1], view=[-L..L, -L..L]);

As a result, we get the result shown in the screenshot. The speed of the load at the moment of impact corresponds to the value given in the preface, and it can be seen that before the thread sags, the load moves in a circle, and after the thread sags, it moves as a free point under the action of gravity, along a parabola.

I note that the error of hitting the nail is a necessary measure: in the polar coordinates that were used, the task has a feature that is clear from equation (8). Therefore, r ( t ) was not compared with zero, but with the value of eps small enough to get a solution, and large enough so that the numerical solver fsolve () does not go crazy. However, this does not detract from the practical value of the results presented.

Instead of conclusion

Perhaps the reader will reproach me for shooting sparrows with a cannon. However, I would like to note that everything complex begins with a simple one, and big science starts with small tasks.

Test version of the library can be downloaded here.

Thank you for your attention to my work)

Source: https://habr.com/ru/post/244957/

All Articles