Hacker's guide to neural networks. Schemes of real values. Strategy number 2: Numerical gradient
Content:
We recall that at the beginning we had a scheme:
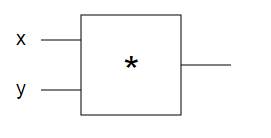
')
Our circuit has one logical element * and several defined initial values (for example, x = -2, y = 3). The logical element computes the result (-6) and we want to change x and y to make the result larger.
What we are going to do is as follows: Imagine that you took the output value, which is obtained from the circuit, and pull it in a positive direction. This positive tension will, in turn, be transmitted through the logical element and apply force to the initial values of x and y. The forces that tell us how x and y should change to increase the resulting value.
How can such forces look on our direct example? We can assume that the force exerted on x should also be positive, since a small increase in x improves the result of the circuit. For example, increasing from x = -2 to x = -1 will result in -3, which is much more than -6. On the other hand, a negative force must appear on y , which will cause it to decrease (since a lower y value, for example, y = 2 , compared to the initial y = 3 , will make the result higher: 2 x -2 = -4 , which again more than -6). In any case, this principle must be remembered. When we move on, it turns out that the forces that I described will actually be a derivative of the output values with respect to their initial values (x and y). You probably already heard this term.
How can we actually evaluate this force (derivative)? It turns out that there is a fairly simple procedure for this. We will work in the opposite direction: instead of stretching the result of the scheme, we will change each initial value in turn, increase it slightly, and see what happens with the result. The number of changes in the output value is the derivative. But for now, theory is enough. Let's look at the mathematical definition. We can write the derivative for our function with respect to the original values. For example, the derivative with respect to x can be calculated as follows:
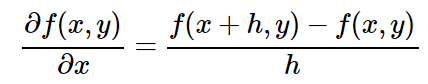
Where h is a small change value. In addition, if you are not particularly familiar with this method of calculation, note that the horizontal line on the left side of the above equation does not mean division. The integer symbol (∂f (x, y)) / ∂x is a single element: the derivative of the function f (x, y) with respect to x. The horizontal line on the right side is the division. I know that it is difficult, but it is a standard notation. In any case, I hope that this does not look too scary.
The scheme produced a certain initial result f (x, y), after which we changed one of the initial values to a small number h and got a new result f (x + h, y). Subtracting these two values shows us the change, and dividing by h simply brings this change to the (arbitrary) value of the change we used. In other words, it expresses exactly what I described above, and translates it into this code:
recall that the forwardMultiplyGate (x, y) function returns the product of arguments
Let's go over the example for x. We turned x into x + h, and the circuit responded with a higher value (again, note that -5.9997> -6). The division by h (in the derivative formula) is performed to bring the result of the circuit to the (arbitrary) value h, which we decided to use in this case. Technically, we need the value of h to be infinitely small (the exact mathematical definition of the gradient is expressed as the limit of expression when h tends to zero), but in practice h = 0.00001 or a similar value is perfect for most cases in which you need to get a good approximation. Now we see that the derivative with respect to x is equal to +3. I specifically indicated a plus sign, as it shows that the circuit pulls x towards a higher value. The actual value of 3 can be interpreted as the force of such tension.
By the way, we usually speak of a derivative with respect to a single initial value, or a gradient with respect to all such values. The gradient consists of the derivatives of all the original values connected to a vector (i.e., a list). Most importantly, if we allow the original values to respond to tension with a small value following the gradient (i.e., we add the derivative only to the upper point of each original value), we can see that it increases, as we expected:
As expected, we changed the original values to a gradient, and the scheme now gives a higher value (-5.87> -6.0). It was a lot easier than trying to arbitrarily change x and y, right? The fact is that if you perform the calculations, you can prove that the gradient is actually the direction of the sharp increase in the function. There is no need to dance with a tambourine, trying to substitute arbitrary values, as we did in strategy # 1. To estimate the gradient, only three estimates of the passage of the circuit are needed instead of a hundred, and we get the optimal impetus we could count on (locally) if we are interested in increasing the output value.
More is not always better. Let me explain a little. Note that in this simple example, using a step size (step_size) greater than 0.01 always gives the best result. For example, step_size = 1.0 results in -1 (larger, better!), And a truly infinite step size can produce an infinitely good result. It is important to understand that as soon as our circuits become significantly more complex (for example, entire neural networks), the functions from source to output values will be more chaotic and “curly”. The gradient ensures that if you have a very small (essentially infinitely small) step size, then you will definitely get a larger number if you proceed in its direction, and for such an infinite small step size there is no other direction that would work just as well. But if you use a larger step (for example, step_size = 0.01), everything will lose its meaning. The reason why we can successfully use the larger step, instead of the infinite small, is that our functions are usually relatively homogeneous. But in fact, we cross our fingers and hope for the best.
Analogy with climbing to the top. I once heard one analogy that the output value of our scheme is like a hill top, and we are trying to climb it blindfolded. We feel the slope of the hill under our feet (gradient), so if we gradually rearrange our legs, we will climb up. But if we take a big and too confident step, we can fall into a hole.
I hope I convinced you that the numerical gradient is really a very useful thing to evaluate, and also quite simple. But. It turns out that we can do even more, which we will discuss in the next part.
We recall that at the beginning we had a scheme:
')
Our circuit has one logical element * and several defined initial values (for example, x = -2, y = 3). The logical element computes the result (-6) and we want to change x and y to make the result larger.
What we are going to do is as follows: Imagine that you took the output value, which is obtained from the circuit, and pull it in a positive direction. This positive tension will, in turn, be transmitted through the logical element and apply force to the initial values of x and y. The forces that tell us how x and y should change to increase the resulting value.
How can such forces look on our direct example? We can assume that the force exerted on x should also be positive, since a small increase in x improves the result of the circuit. For example, increasing from x = -2 to x = -1 will result in -3, which is much more than -6. On the other hand, a negative force must appear on y , which will cause it to decrease (since a lower y value, for example, y = 2 , compared to the initial y = 3 , will make the result higher: 2 x -2 = -4 , which again more than -6). In any case, this principle must be remembered. When we move on, it turns out that the forces that I described will actually be a derivative of the output values with respect to their initial values (x and y). You probably already heard this term.
The derivative can be considered as a force acting on each initial value as we increase the resulting value.
How can we actually evaluate this force (derivative)? It turns out that there is a fairly simple procedure for this. We will work in the opposite direction: instead of stretching the result of the scheme, we will change each initial value in turn, increase it slightly, and see what happens with the result. The number of changes in the output value is the derivative. But for now, theory is enough. Let's look at the mathematical definition. We can write the derivative for our function with respect to the original values. For example, the derivative with respect to x can be calculated as follows:
Where h is a small change value. In addition, if you are not particularly familiar with this method of calculation, note that the horizontal line on the left side of the above equation does not mean division. The integer symbol (∂f (x, y)) / ∂x is a single element: the derivative of the function f (x, y) with respect to x. The horizontal line on the right side is the division. I know that it is difficult, but it is a standard notation. In any case, I hope that this does not look too scary.
The scheme produced a certain initial result f (x, y), after which we changed one of the initial values to a small number h and got a new result f (x + h, y). Subtracting these two values shows us the change, and dividing by h simply brings this change to the (arbitrary) value of the change we used. In other words, it expresses exactly what I described above, and translates it into this code:
recall that the forwardMultiplyGate (x, y) function returns the product of arguments
var x = -2, y = 3; var out = forwardMultiplyGate(x, y); // -6 var h = 0.0001; // x var xph = x + h; // -1.9999 var out2 = forwardMultiplyGate(xph, y); // -5.9997 var x_derivative = (out2 - out) / h; // 3.0 // y var yph = y + h; // 3.0001 var out3 = forwardMultiplyGate(x, yph); // -6.0002 var y_derivative = (out3 - out) / h; // -2.0 Let's go over the example for x. We turned x into x + h, and the circuit responded with a higher value (again, note that -5.9997> -6). The division by h (in the derivative formula) is performed to bring the result of the circuit to the (arbitrary) value h, which we decided to use in this case. Technically, we need the value of h to be infinitely small (the exact mathematical definition of the gradient is expressed as the limit of expression when h tends to zero), but in practice h = 0.00001 or a similar value is perfect for most cases in which you need to get a good approximation. Now we see that the derivative with respect to x is equal to +3. I specifically indicated a plus sign, as it shows that the circuit pulls x towards a higher value. The actual value of 3 can be interpreted as the force of such tension.
The derivative with respect to any initial value can be calculated by adjusting such an initial value by a small number and observing the change in the output value.
By the way, we usually speak of a derivative with respect to a single initial value, or a gradient with respect to all such values. The gradient consists of the derivatives of all the original values connected to a vector (i.e., a list). Most importantly, if we allow the original values to respond to tension with a small value following the gradient (i.e., we add the derivative only to the upper point of each original value), we can see that it increases, as we expected:
var step_size = 0.01; var out = forwardMultiplyGate(x, y); // : -6 x = x + step_size * x_derivative; // x -1.97 y = y + step_size * y_derivative; // y 2.98 var out_new = forwardMultiplyGate(x, y); // -5.87! As expected, we changed the original values to a gradient, and the scheme now gives a higher value (-5.87> -6.0). It was a lot easier than trying to arbitrarily change x and y, right? The fact is that if you perform the calculations, you can prove that the gradient is actually the direction of the sharp increase in the function. There is no need to dance with a tambourine, trying to substitute arbitrary values, as we did in strategy # 1. To estimate the gradient, only three estimates of the passage of the circuit are needed instead of a hundred, and we get the optimal impetus we could count on (locally) if we are interested in increasing the output value.
More is not always better. Let me explain a little. Note that in this simple example, using a step size (step_size) greater than 0.01 always gives the best result. For example, step_size = 1.0 results in -1 (larger, better!), And a truly infinite step size can produce an infinitely good result. It is important to understand that as soon as our circuits become significantly more complex (for example, entire neural networks), the functions from source to output values will be more chaotic and “curly”. The gradient ensures that if you have a very small (essentially infinitely small) step size, then you will definitely get a larger number if you proceed in its direction, and for such an infinite small step size there is no other direction that would work just as well. But if you use a larger step (for example, step_size = 0.01), everything will lose its meaning. The reason why we can successfully use the larger step, instead of the infinite small, is that our functions are usually relatively homogeneous. But in fact, we cross our fingers and hope for the best.
Analogy with climbing to the top. I once heard one analogy that the output value of our scheme is like a hill top, and we are trying to climb it blindfolded. We feel the slope of the hill under our feet (gradient), so if we gradually rearrange our legs, we will climb up. But if we take a big and too confident step, we can fall into a hole.
I hope I convinced you that the numerical gradient is really a very useful thing to evaluate, and also quite simple. But. It turns out that we can do even more, which we will discuss in the next part.
Source: https://habr.com/ru/post/244935/
All Articles