Hacker's guide to neural networks. Schemes of real values. Strategy # 1: Random local search
We are starting to publish the translation of the book (as the author calls it) “Hacker's Guide to Neural Networks”. The book consists of four parts, two of which have already been completed. We will try to break the text into logically complete parts, the size of which will allow not overloading the reader. We will also follow the update of the book and publish the translation of new parts after they appear in the author's blog.
Content:
Hi there, I'm a graduate student in computing at Stanford. For several years, as part of my research, I have been working on in-depth training, and among several related my favorite projects - ConvNetJS - Javascript library for training neural networks. Javascript allows you to visualize well what is happening, and gives you the opportunity to understand the various settings of the hyperparameters, but I still regularly hear people want to consider this topic in more detail. This article (which I plan to gradually expand to the volume of several chapters) is my modest attempt to do so. I post it online, instead of creating it in PDF format, as I should do with books, because it should (and I hope it will) end up with animations / demos, etc.
My personal experience with neural networks shows that everything becomes much clearer when I start to ignore full page spreads, dense derivatives of back-propagation errors, and just start writing code. Therefore, this manual will contain very little mathematics (I don’t think it is necessary, and in some places it may even complicate the understanding of simple concepts). Since my specialty is computer science and physics, I, instead, will develop this topic from the point of view of a hacker. My presentation will be centered around code and physical intuition, instead of mathematical derivatives. Basically, I will try to present the algorithms in the way I would like to use when I first started.
')
Surely you will want to skip and immediately begin to study neural networks, how to use them in practice, etc. But before we take up this, I would like us to forget about all this. Let's take a step back and see what, in fact, is happening. Let's first talk about real-world value schemes.
Chapter 1: Real Value Schemes
In my opinion, the best way to imagine neural networks is as real-world value schemes in which real values (instead of Boolean {0,1}) “flow” along boundaries and interact in logical elements. However, instead of such logical elements as AND, OR, NOT, etc., we have binary logical elements, such as * (multiply), + (add), max, or unary logic elements, such as exp, etc. However in contrast to conventional boolean schemes, we will eventually also have gradients flowing along the same boundaries of the scheme, but in the opposite direction. But we are running ahead. Let's concentrate and start simple.
Basic scenario: Simple logical element in the scheme
Let's first consider a single simple circuit with one logical element. Here is an example:
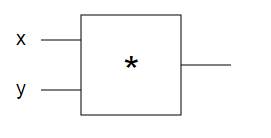
The circuit takes two source real values x and y and multiplies x * y with the aid of a logical element *.
The javascript version of this equation will look very simple, like this:
And in the mathematical form, we can consider this logical element as a reproduction of a function with real values:
f (x, y) = xy
As in this example, all our logical elements will take one or two initial values and produce one output value.
purpose
The problem, the study of which interests us, is as follows:
1. We enter certain initial values into the given scheme (for example, x = -2, y = 3)
2. The circuit calculates the output value (for example, -6)
3. As a result, the key question arises: How should the initial value be slightly changed to increase the result?
In this case, which way should we change x, y to get a number greater than -6? Note that, for example, x = -1.99 and y = 2.99 results in x * y = -5.95, which is already greater than -6.0. Do not worry: -5.95 is better (higher) than -6.0. This is an improvement of 0.05, even though the value of -5.95 (distance from zero) is sometimes lower.
Strategy # 1: Random local search
Good. We have a circuit, we have several source values, and we just need to change them a bit to increase the output value? What is the difficulty? We can easily “help” the scheme to calculate the result for any given x and y value. Isn't it easy? Why not change x and y arbitrarily and not track which of the changes gives the best result:
When I started it, I got best_x = -1.9928, best_y = 2.9901, and best_out = -5.9588. Again, -5.9588 is higher than -6.0. Well, we are done, right? Not really: This is the ideal strategy for small problems with a small number of logical elements, if you have the time to calculate, but it does not work if we want to deal with large circuits with millions of initial values. It turns out we can do more, but more on that in the next part.
Content:
Hi there, I'm a graduate student in computing at Stanford. For several years, as part of my research, I have been working on in-depth training, and among several related my favorite projects - ConvNetJS - Javascript library for training neural networks. Javascript allows you to visualize well what is happening, and gives you the opportunity to understand the various settings of the hyperparameters, but I still regularly hear people want to consider this topic in more detail. This article (which I plan to gradually expand to the volume of several chapters) is my modest attempt to do so. I post it online, instead of creating it in PDF format, as I should do with books, because it should (and I hope it will) end up with animations / demos, etc.
My personal experience with neural networks shows that everything becomes much clearer when I start to ignore full page spreads, dense derivatives of back-propagation errors, and just start writing code. Therefore, this manual will contain very little mathematics (I don’t think it is necessary, and in some places it may even complicate the understanding of simple concepts). Since my specialty is computer science and physics, I, instead, will develop this topic from the point of view of a hacker. My presentation will be centered around code and physical intuition, instead of mathematical derivatives. Basically, I will try to present the algorithms in the way I would like to use when I first started.
')
"... everything became much clearer when I started writing code"
Surely you will want to skip and immediately begin to study neural networks, how to use them in practice, etc. But before we take up this, I would like us to forget about all this. Let's take a step back and see what, in fact, is happening. Let's first talk about real-world value schemes.
Chapter 1: Real Value Schemes
In my opinion, the best way to imagine neural networks is as real-world value schemes in which real values (instead of Boolean {0,1}) “flow” along boundaries and interact in logical elements. However, instead of such logical elements as AND, OR, NOT, etc., we have binary logical elements, such as * (multiply), + (add), max, or unary logic elements, such as exp, etc. However in contrast to conventional boolean schemes, we will eventually also have gradients flowing along the same boundaries of the scheme, but in the opposite direction. But we are running ahead. Let's concentrate and start simple.
Basic scenario: Simple logical element in the scheme
Let's first consider a single simple circuit with one logical element. Here is an example:
The circuit takes two source real values x and y and multiplies x * y with the aid of a logical element *.
The javascript version of this equation will look very simple, like this:
var forwardMultiplyGate = function(x, y) { return x * y; }; forwardMultiplyGate(-2, 3); // returns -6. And in the mathematical form, we can consider this logical element as a reproduction of a function with real values:
f (x, y) = xy
As in this example, all our logical elements will take one or two initial values and produce one output value.
purpose
The problem, the study of which interests us, is as follows:
1. We enter certain initial values into the given scheme (for example, x = -2, y = 3)
2. The circuit calculates the output value (for example, -6)
3. As a result, the key question arises: How should the initial value be slightly changed to increase the result?
In this case, which way should we change x, y to get a number greater than -6? Note that, for example, x = -1.99 and y = 2.99 results in x * y = -5.95, which is already greater than -6.0. Do not worry: -5.95 is better (higher) than -6.0. This is an improvement of 0.05, even though the value of -5.95 (distance from zero) is sometimes lower.
Strategy # 1: Random local search
Good. We have a circuit, we have several source values, and we just need to change them a bit to increase the output value? What is the difficulty? We can easily “help” the scheme to calculate the result for any given x and y value. Isn't it easy? Why not change x and y arbitrarily and not track which of the changes gives the best result:
// , var forwardMultiplyGate = function(x, y) { return x * y; }; var x = -2, y = 3; // some input values // x,y , var tweak_amount = 0.01; var best_out = -Infinity; var best_x = x, best_y = y; for(var k = 0; k < 100; k++) { var x_try = x + tweak_amount * (Math.random() * 2 - 1); // x var y_try = y + tweak_amount * (Math.random() * 2 - 1); // y var out = forwardMultiplyGate(x_try, y_try); if(out > best_out) { // ! x y best_out = out; best_x = x_try, best_y = y_try; } } When I started it, I got best_x = -1.9928, best_y = 2.9901, and best_out = -5.9588. Again, -5.9588 is higher than -6.0. Well, we are done, right? Not really: This is the ideal strategy for small problems with a small number of logical elements, if you have the time to calculate, but it does not work if we want to deal with large circuits with millions of initial values. It turns out we can do more, but more on that in the next part.
Source: https://habr.com/ru/post/244723/
All Articles