How I drove Balda on Visual Basic for Applications for MS Access
I do not remember what I was stuck with. Probably, someone beat me in Baldu with a crushing score (its online version is on Odnoklassniki, Mail.ru and in a bunch of other places). In short, I accepted the challenge. Last time it was with the program for solving the SUDOKU. But everything turned out to be noticeably simpler there.
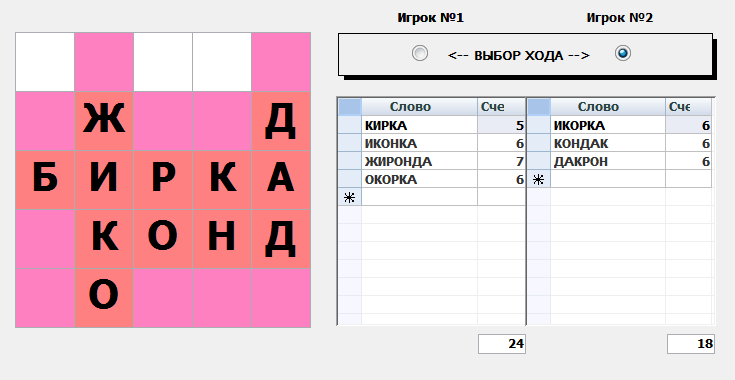
Balda, she's the Magic Square. Players add one letter at a time to make a meaningful word as long as possible.
Being a programmer of the old school (FORTRAN, PL1 and a stack of punched cards), I believe that it really doesn’t matter what to write the code on. From the cardinal ideas that happened in the history of programming, it is worth mentioning only object orientation and the relational data model (well, perhaps, functional programming, all sorts of lambda-things, as opposed to the usual procedural approach). The main thing, nevertheless, is the Algorithm! Which are all mainly set out in the seven-volume “Basics of Programming” by Donald Knuth. And which teams will draw you a window, an icon and other charms is the tenth thing. Knut's seven-volume book, like the base article on Edgar Codd's relational bases from the IBM Research Center, appeared in the second half of the 60s. That is almost half a century ago. That is why I write in VBA and do not get distracted by any newfangled things.
There were actually two calls (I don’t like this tracing from the English challenge, but I’m used to it!) When I wrote the game. Correctly register the recursive algorithm, and then optimize the search for words in the dictionary.
')
With the algorithm itself, everything is quite simple. Here there is a playing field 5 by 5 with the letters already entered. You need to add one more letter adjacent to the existing one from any side (except diagonally), and look through the dictionary for all the variations of words that appear with all possible variants of “walking around” the playing field filled with letters. This is where recursion occurs.
We start in order with any letter and go in any direction, where there is another letter. So the word is typed for verification. The letters themselves, already included in the word to be checked, should be excluded from further checks, since the word cannot be with intersections (it is impossible to use the same letter 2 times).
The typed character string at each stage is searched in the dictionary. If the word is found, we remember this option, but continue the search without interrupting the recursion, since there may be a longer word with the same beginning (having found the CAT, we do not miss the chance to find also CATOVASIA, CATTING, etc.)
The signal to exit recursion (this, as we remember, the most important part in writing recursive functions) is simply the inability to choose another letter when all possible moves in a given step are exhausted (already included in the word to be tested or out of reach of the playing field, where we were at this step). Then we make a way out, that is, we step back a step and try to move in the other direction. A complete exit from recursion will occur when we iterate through all possible options - all paths bypassing the field with letters.
At the same time, the newly added letter should fall into the word we are checking. But this rule cannot be included a priori - it may be that this letter will turn out to be the last, so this check needs to be done only at the very end, before searching in the dictionary.
In this place I was surprised by the number of options that arise. In the midst of the game (when the playing field is already full, but there are enough free cells), the system scans over 100,000 (in words - one hundred thousand) variants of words at every step! We are clearly dealing with a problem of exponential complexity on the size of the field (NP-completeness?). Therefore, from the original idea - to calculate every game for many moves ahead, in order to choose the option that does not give the enemy long words in his turn (assuming, of course, that we use the same vocabulary!) Had to be abandoned.
By the way, the depth of recursion is quite small - as is clear from the described algorithm, it does not exceed the number of letters on the field at the moment.
I took Zaliznyak's dictionary as a dictionary (this is the same linguist who whose tables on the morphology of the Russian language and word forms were based on the syntax check in Microsoft Word 6.0 by Igor Agamirzyan). According to the Baldy rules, only nouns in the nominative singular can be used, such as in the dictionary I used was exactly 43,304, from "ABAZHURA" to "LIZHURA".
So, we have one hundred thousand variants of words (at the peak - up to 150,000), which should be searched in a dictionary of 43,304 words. It comes out more than six billion views of the dictionary, if I'm not mistaken in the calculations. The first version of the program was conceived over each move for several minutes, and this disgrace could not, of course, be tolerated. Not to mention the fact that if you use the program to fight a real rival, it’s not more than a minute to think about the move. And I also want to look at least one step ahead, so as not to substitute any super long word to the enemy in his turn.
So optimization. First, all work should be carried out only in RAM, the amount of data it allows. The entire dictionary is read from a table into an array, which is then searched. But this is clearly not enough.
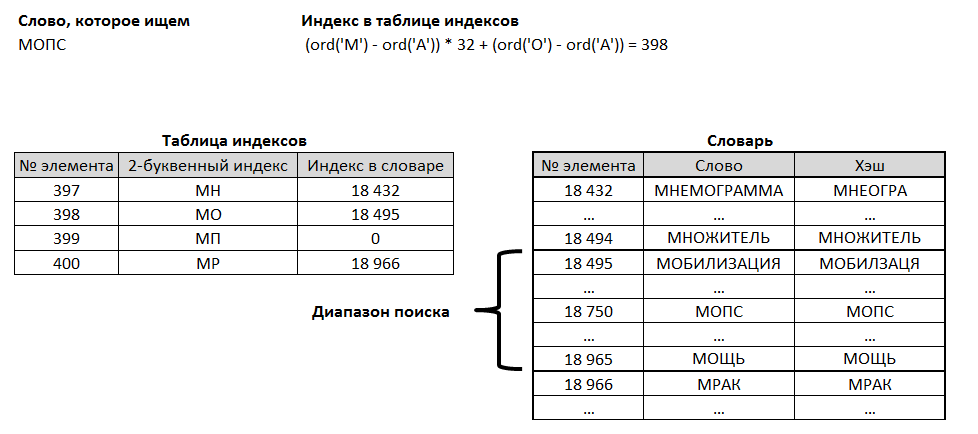
The second clear way to optimize is indexing. I made it in a 2-letter version. In a separate array, consisting of all possible two-letter pairs, an index was entered, starting with which the words beginning with these same 2 letters are located in the array with a complete dictionary. In order not to search for the first 2 letters in the array of indexes, it was made complete, that is, it contained even those pairs of letters for which there is not a single word in the dictionary. Thus, the index in the array of indices was calculated directly from the first 2 letters of the word we are looking for, that is, very quickly.
The array of indexes also does not take up much space in memory, its length is 32 x 32 = 1024 elements. Actually, it was easy to make the index and 3-letter, but this, as experience has shown, did not lead to further acceleration.
This is not all optimization! I also expanded the source dictionary with some hash, if you can call it that - in fact, it was the same word, but in which each letter was found only once (POTOP - VET). As a result, the fastest search option turned out to be:
- we iterate over the full dictionary, leaving only those words that contain the same letters as in the word we are looking for;
- we build on this truncated dictionary a 2-letter index;
- we are looking for the desired word using the index.
The result - the search for all variants of words on each turn takes no more than 2 seconds, while, as I said, up to 150,000 words in the dictionary are viewed and up to a hundred variants of the course are displayed - words from 4-letter or higher. It is also possible for each word option found to calculate the possible future moves of the opponent - at a price of 2 seconds for one option.
Now about MS Access. I am endlessly in love with this program, as it combines a quite tolerable relational database engine, simple interface building, and a powerful Visual Basic for Applications behind the scenes.
The latter, they say, is not inferior to C ++ / C # in the speed of processing string information - which was demonstrated by the optimization of our program.
As for the database, this, I believe, is the only correct data storage format, on which there is at least some kind of structure. It also allows you to write programs "with accumulation" - that is, such, the calculation for which takes many days (these are all sorts of linguistic tasks that I sometimes indulge in). In order not to lose intermediate results, it is correct to discard them into tables with a certain regularity, which does not slow down the execution of basic calculations. That there was always some starting point from which to proceed.
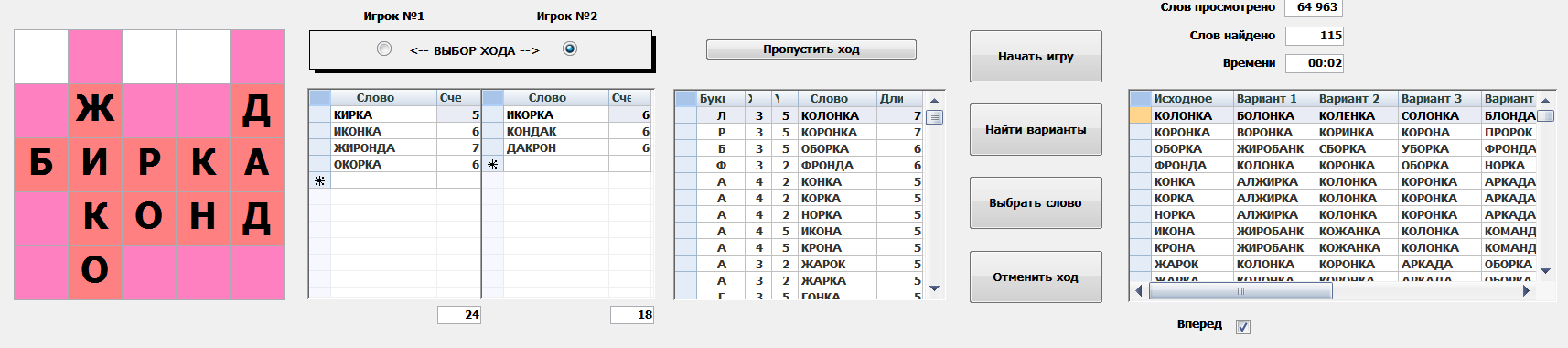
Program interface The system offers all options of moves, sorted in descending order of length. If you wish, you can look ahead to the next possible move of the opponent when you choose one or another word variant.

And this is how the match with the opponent looks like. You need to carefully make his moves, and the program will tell you the best option.
Want to scold me for dishonesty? But I wrote and optimized the program myself! Moreover, he played for the interest, and not for the sake of any benefits. Moreover, almost all rivals use something similar, but they are not written by themselves - this is immediately apparent. Where does the 15-year-old guy, whose profile is full of photos with cats, come from, know the word PROZELITISM? (“What does baby Tiffany do in an unfavorable area at one o'clock with a textbook of quantum physics in her hands?”)

Balda, she's the Magic Square. Players add one letter at a time to make a meaningful word as long as possible.
Being a programmer of the old school (FORTRAN, PL1 and a stack of punched cards), I believe that it really doesn’t matter what to write the code on. From the cardinal ideas that happened in the history of programming, it is worth mentioning only object orientation and the relational data model (well, perhaps, functional programming, all sorts of lambda-things, as opposed to the usual procedural approach). The main thing, nevertheless, is the Algorithm! Which are all mainly set out in the seven-volume “Basics of Programming” by Donald Knuth. And which teams will draw you a window, an icon and other charms is the tenth thing. Knut's seven-volume book, like the base article on Edgar Codd's relational bases from the IBM Research Center, appeared in the second half of the 60s. That is almost half a century ago. That is why I write in VBA and do not get distracted by any newfangled things.
There were actually two calls (I don’t like this tracing from the English challenge, but I’m used to it!) When I wrote the game. Correctly register the recursive algorithm, and then optimize the search for words in the dictionary.
')
With the algorithm itself, everything is quite simple. Here there is a playing field 5 by 5 with the letters already entered. You need to add one more letter adjacent to the existing one from any side (except diagonally), and look through the dictionary for all the variations of words that appear with all possible variants of “walking around” the playing field filled with letters. This is where recursion occurs.
We start in order with any letter and go in any direction, where there is another letter. So the word is typed for verification. The letters themselves, already included in the word to be checked, should be excluded from further checks, since the word cannot be with intersections (it is impossible to use the same letter 2 times).
The typed character string at each stage is searched in the dictionary. If the word is found, we remember this option, but continue the search without interrupting the recursion, since there may be a longer word with the same beginning (having found the CAT, we do not miss the chance to find also CATOVASIA, CATTING, etc.)
The signal to exit recursion (this, as we remember, the most important part in writing recursive functions) is simply the inability to choose another letter when all possible moves in a given step are exhausted (already included in the word to be tested or out of reach of the playing field, where we were at this step). Then we make a way out, that is, we step back a step and try to move in the other direction. A complete exit from recursion will occur when we iterate through all possible options - all paths bypassing the field with letters.
At the same time, the newly added letter should fall into the word we are checking. But this rule cannot be included a priori - it may be that this letter will turn out to be the last, so this check needs to be done only at the very end, before searching in the dictionary.
In this place I was surprised by the number of options that arise. In the midst of the game (when the playing field is already full, but there are enough free cells), the system scans over 100,000 (in words - one hundred thousand) variants of words at every step! We are clearly dealing with a problem of exponential complexity on the size of the field (NP-completeness?). Therefore, from the original idea - to calculate every game for many moves ahead, in order to choose the option that does not give the enemy long words in his turn (assuming, of course, that we use the same vocabulary!) Had to be abandoned.
By the way, the depth of recursion is quite small - as is clear from the described algorithm, it does not exceed the number of letters on the field at the moment.
I took Zaliznyak's dictionary as a dictionary (this is the same linguist who whose tables on the morphology of the Russian language and word forms were based on the syntax check in Microsoft Word 6.0 by Igor Agamirzyan). According to the Baldy rules, only nouns in the nominative singular can be used, such as in the dictionary I used was exactly 43,304, from "ABAZHURA" to "LIZHURA".
So, we have one hundred thousand variants of words (at the peak - up to 150,000), which should be searched in a dictionary of 43,304 words. It comes out more than six billion views of the dictionary, if I'm not mistaken in the calculations. The first version of the program was conceived over each move for several minutes, and this disgrace could not, of course, be tolerated. Not to mention the fact that if you use the program to fight a real rival, it’s not more than a minute to think about the move. And I also want to look at least one step ahead, so as not to substitute any super long word to the enemy in his turn.
So optimization. First, all work should be carried out only in RAM, the amount of data it allows. The entire dictionary is read from a table into an array, which is then searched. But this is clearly not enough.
The second clear way to optimize is indexing. I made it in a 2-letter version. In a separate array, consisting of all possible two-letter pairs, an index was entered, starting with which the words beginning with these same 2 letters are located in the array with a complete dictionary. In order not to search for the first 2 letters in the array of indexes, it was made complete, that is, it contained even those pairs of letters for which there is not a single word in the dictionary. Thus, the index in the array of indices was calculated directly from the first 2 letters of the word we are looking for, that is, very quickly.
The array of indexes also does not take up much space in memory, its length is 32 x 32 = 1024 elements. Actually, it was easy to make the index and 3-letter, but this, as experience has shown, did not lead to further acceleration.
This is not all optimization! I also expanded the source dictionary with some hash, if you can call it that - in fact, it was the same word, but in which each letter was found only once (POTOP - VET). As a result, the fastest search option turned out to be:
- we iterate over the full dictionary, leaving only those words that contain the same letters as in the word we are looking for;
- we build on this truncated dictionary a 2-letter index;
- we are looking for the desired word using the index.

The result - the search for all variants of words on each turn takes no more than 2 seconds, while, as I said, up to 150,000 words in the dictionary are viewed and up to a hundred variants of the course are displayed - words from 4-letter or higher. It is also possible for each word option found to calculate the possible future moves of the opponent - at a price of 2 seconds for one option.
Now about MS Access. I am endlessly in love with this program, as it combines a quite tolerable relational database engine, simple interface building, and a powerful Visual Basic for Applications behind the scenes.
The latter, they say, is not inferior to C ++ / C # in the speed of processing string information - which was demonstrated by the optimization of our program.
As for the database, this, I believe, is the only correct data storage format, on which there is at least some kind of structure. It also allows you to write programs "with accumulation" - that is, such, the calculation for which takes many days (these are all sorts of linguistic tasks that I sometimes indulge in). In order not to lose intermediate results, it is correct to discard them into tables with a certain regularity, which does not slow down the execution of basic calculations. That there was always some starting point from which to proceed.

Program interface The system offers all options of moves, sorted in descending order of length. If you wish, you can look ahead to the next possible move of the opponent when you choose one or another word variant.
And this is how the match with the opponent looks like. You need to carefully make his moves, and the program will tell you the best option.
Want to scold me for dishonesty? But I wrote and optimized the program myself! Moreover, he played for the interest, and not for the sake of any benefits. Moreover, almost all rivals use something similar, but they are not written by themselves - this is immediately apparent. Where does the 15-year-old guy, whose profile is full of photos with cats, come from, know the word PROZELITISM? (“What does baby Tiffany do in an unfavorable area at one o'clock with a textbook of quantum physics in her hands?”)
Source: https://habr.com/ru/post/244217/
All Articles