Analyze friendships VK using Python. Continuation
In the previous article, we built a graph on the basis of mutual friends on VKontakte, and today we will talk about how to get a list of friends, friends of friends, and so on. It is assumed that you have already read the previous article , and I will not describe everything anew. Habrakat large pictures and a lot of text.
To begin with, simply downloading all user id's is easy enough; a list of valid id can be found in the Vkontakte User Catalog . Our task is to get a list of friends of our chosen user id, their friends, and recursively as much as desired, depending on the specified depth.
The code published in the article will change over time, so a more recent version can be found in the same project on Github .
How we will implement:
What we will use:
What we need at the beginning is to indicate the depth ( deep ) with which we want to work. This can be done immediately in settings.py :
')
deep equal to 1 is our friends, 2 is friends of our friends and so on. As a result, we get a dictionary, the keys of which are the users' id, and the values are their list of friends.
Do not rush to set a large depth. With 14 of my original friends and a depth of 2, the number of keys in the dictionary was 2427, and with a depth of 3, I didn’t have the patience to wait for the script to finish, at that time the dictionary had 223,908 keys. For this reason, we will not visualize such a huge graph, because the vertices are the keys, and the edges are the values.
The already known friends.get method, which will be located in a stored procedure that has the following form, will help us achieve the result we need:
I remind you that you can create a stored procedure in the application settings , it is written in VkScript , as well as execute , the documentation can be read here and here .
Now how it works. We accept a string of 25 id, separated by commas, take out one id, make a request to friends.get , and the information we need will come in the dictionary, where the keys are id, and the values are a list of friends of this id.
When you first start, we will send to the stored procedure a list of friends of the current user whose id is specified in the settings. The list will be divided into several parts (N / 25 - this is also the number of requests), this is due to the limitation of the number of calls to the VKontakte API.
We store all received information in a dictionary, for example:
The keys 1, 2 and 3 were obtained with a depth equal to 1. Suppose that these were all the friends of the specified user (0).
If the depth is greater than 1, then we use the difference of sets, the first of which is the dictionary values, and the second is its keys. Thus, we get those id (in this case, 0 and 4), which are not in the keys, divide them again into 25 parts and send to the stored procedure.
Then in our dictionary there will be 2 new keys:
The very method deep_friends () looks like this:
Of course, this is faster than throwing one id at friends.get without using a stored procedure, but it still takes a lot of time.
If friends.get were similar to users.get , namely, it could take user_ids as a parameter, that is, id listed by comma, for which you need to return a list of friends, rather than one id, then the code would be much simpler, and The number of requests was several times less.
Returning to the beginning of the article, I can repeat it again - very slowly. Stored procedures do not save, the alxpy solution with multithreading (thanks to him for his contribution and participationat least someone was interested, except for me ) accelerated the program for a few seconds, but wanted more.
Wise advice received from igrishaev - we need some kind of map.
The fact is that VKontakte resolves 25 requests to the API through execute , it follows from this that if we make requests from different clients, we can increase the number of valid requests. 5 wheelbarrows - this is 125 requests per second. But this is far from the case. Looking ahead, I will say that it is possible and even faster, it will look something like this (on each machine):
If we receive an error message, we make a request again, after a specified number of seconds. This technique works for some time, but then VKontakte starts to send None in all answers, so after each request we honestly wait for 1 second. For now.
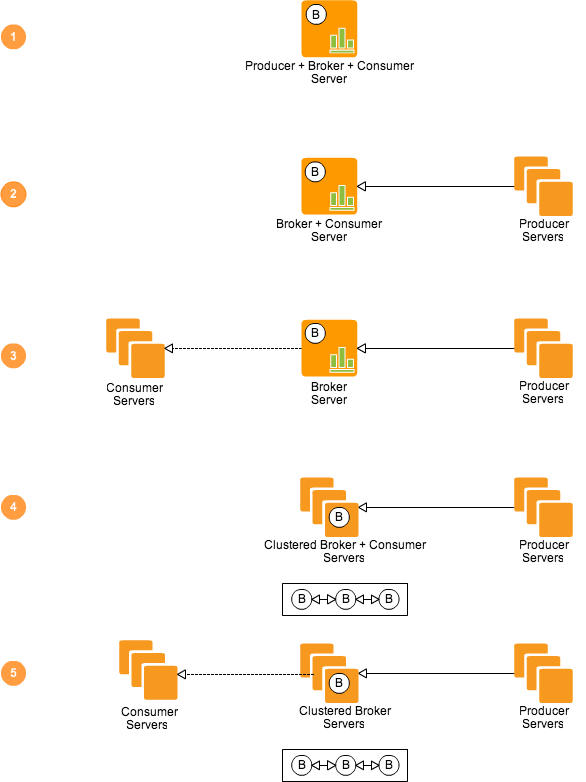
Next, we need to choose new tools or write our own to realize our plans. As a result, we should have a horizontally scalable system, the principle of operation seems to me as follows:
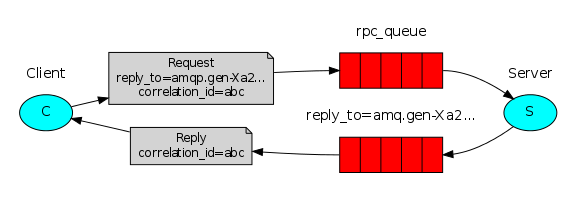
And if you saw this picture, then you understand what message broker I am hinting at.
Once all the answers are accepted, we merge them into one. Further, the result can be displayed on the screen or even saved, more on that later.
Here it is worth noting that the code will change, and if it was enough for you to use the previous version of the project, then it remained unchanged. All the code below will be for the new release.
As a message broker, we will use RabbitMQ , an asynchronous distributed job queue - Celery .
For those who have never come across them, here are some useful links to materials that I advise you to read:
Do not be afraid to understand, although they say that you can specifically turn your head when you start to “think not with one computer, but with several”, but this is not at all the case.
If you have a Mac, like the author, then RabbitMQ is smartly installed via Homebrew :
Celery is put even easier, we use the third branch of Python :
I have Celery installed on Linux Mint, and RabbitMQ on Mac. With Windows, as usual, the problems arehard to find, it is easy to lose , for some reason, she didn’t always want to return the response to my Mac.
Next, create a virtual host , user, and give him the right:
In the RabbitMQ configuration, you must specify the ip of the host on which it is installed:
Here are some possible configurations, which one to choose is up to you.
If you have a router or something else, it will be useful to know that RabbitMQ uses port 5672, well, and make redirection in the settings of your device. Most likely, if you test, you scatter the workers on different machines, and they will need to use a broker, and if you don’t correctly set up the network, Celery will not reach RabbitMQ .
Very good news is that VKontakte allows you to do 3 requests per second from one id. Multiply these requests by the number of possible calls to the VKontakte API (25), we get the maximum number of contacts processed per second (75).

If we have a lot of workers, then the moment will come when we begin to go beyond the allowed limit. Therefore, the token variable (in settings.py ) will now be a tuple containing several tokens from different id. At each request to the VK API, the script will choose one of them in a random way:
In this regard, you should have no difficulties if there are several accounts on VKontakte (you can strain friends, relatives), I did not have problems with 4 tokens and 3 workers.
No, no one bothers you to use time.sleep () , or the example above with while, but then get ready to receive error messages (empty answers are possible at all - id: None), or wait a little longer.
The most interesting from the file call.py :
As you can see, in 2 functions we use groups () , which runs several tasks in parallel, after which we “glue” the answer. Remember how deep_friends () looked at the beginning (there’s a very old example - even without multithreading)? The meaning remains the same - we use the set difference.
And finally, tasks.py . Someday these great features will merge into one:
When everything is set up, run RabbitMQ with the command:
Then go to the project folder and activate the worker:
Now, to get and save a list of common or "deep" friends, just command in the console:
Let me remind you that the author of the article , which inspired me to the first part , had 343 friends (a request for mutual friends) “processed” in 119 seconds .
My version of the previous article did the same thing in 9 seconds .
Now that author has a different number of friends - 308. Well, you have to make one extra request for the last eight id, spend a precious second on it, although you can process 75 id in that second.
With one worker, the script took 4.2 seconds , and with two workers, 2.2 seconds .
If 119 is round to 120, and 2.2 to 2, then my version works 60 times faster .
As for the “deep friends” (friends of my friends and so on + we test on another id to wait less) - with a depth equal to 2, the number of keys in the dictionary was 1,251.
The execution time of the code given at the very beginning of the article is 17.9 seconds .
With one worker, the script execution time is 15.1 seconds , with two workers, 8.2 seconds .
Thus, deep_friends () has become about 2.18 times faster.
Yes, the result is not always so bright, sometimes you have to wait 10 or 20 seconds for a response to one VKontakte (although the frequent execution time of one task is 1.2 - 1.6 seconds ), most likely, this is due to the load on the service, because we not alone in the universe.

As a result, the more workers do, the faster the result will be processed. Do not forget about the power of your hardware, additional tokens, the network (for example, the author dramatically increased the script execution time when he used his iPhone as an access point) and other factors.
Yes, there are a lot of graph-oriented databases. If in the future (and it will be so), we want to analyze the results obtained, then all the same they will need to be stored somewhere until the analysis itself, then the same results should be uploaded to the memory and some actions should be taken with them. I see no reason to use any subd, if the project would be commercial and we were interested in, for example, what happens to the graph of a particular user over time - then yes, then the graph-oriented database is obligatory, but since we will be engaged in the analysis at home “ Pickle is enough for us.
Before saving dictionaries, it will be logical to delete from them keys whose values are None . These are blocked or deleted accounts. Simply put, these id will be in the column, because they have someone as friends, well, we will save on the number of keys in the dictionary:
As you can see, if we save the result somewhere, then we need to load it somewhere in order not to collect the id again.
In order not to write your bike, let's use a fairly well-known networkx , which will do all thedirty work for us. You can learn more about networkx from this article .
Before we begin to analyze the graph, draw it. networkx for this you need matplotlib :
Next we need to create the graph itself. In general, there are 2 ways.
The first will eat a lot of RAM and your time:
And this is not the author has survived the mind, no. A similar example is given on the Rice University page , under the heading Convert Dictionary Graph Representation into networkx Graph Representation :
You can take my word for it, the count was being built the whole evening, when there were already more than 300,000 peaks in it, my patience snapped.If you completed a course on oursera on Python from this university, then you know what I mean. And I told everyone on the course that people do not teach this, but oh well.
Yes, an example is given for a directed graph, but the essence remains the same - first we add keys, making them vertices, then making vertices of the values, and then if they are not already in the graph, and then we connect them with edges (in my version).
And the second method will do everything in seconds:
The code lies in the graph.py file, to draw a graph of mutual friends, just run this script or create an instance of the VkGraph () class somewhere and then call its draw_graph () method.
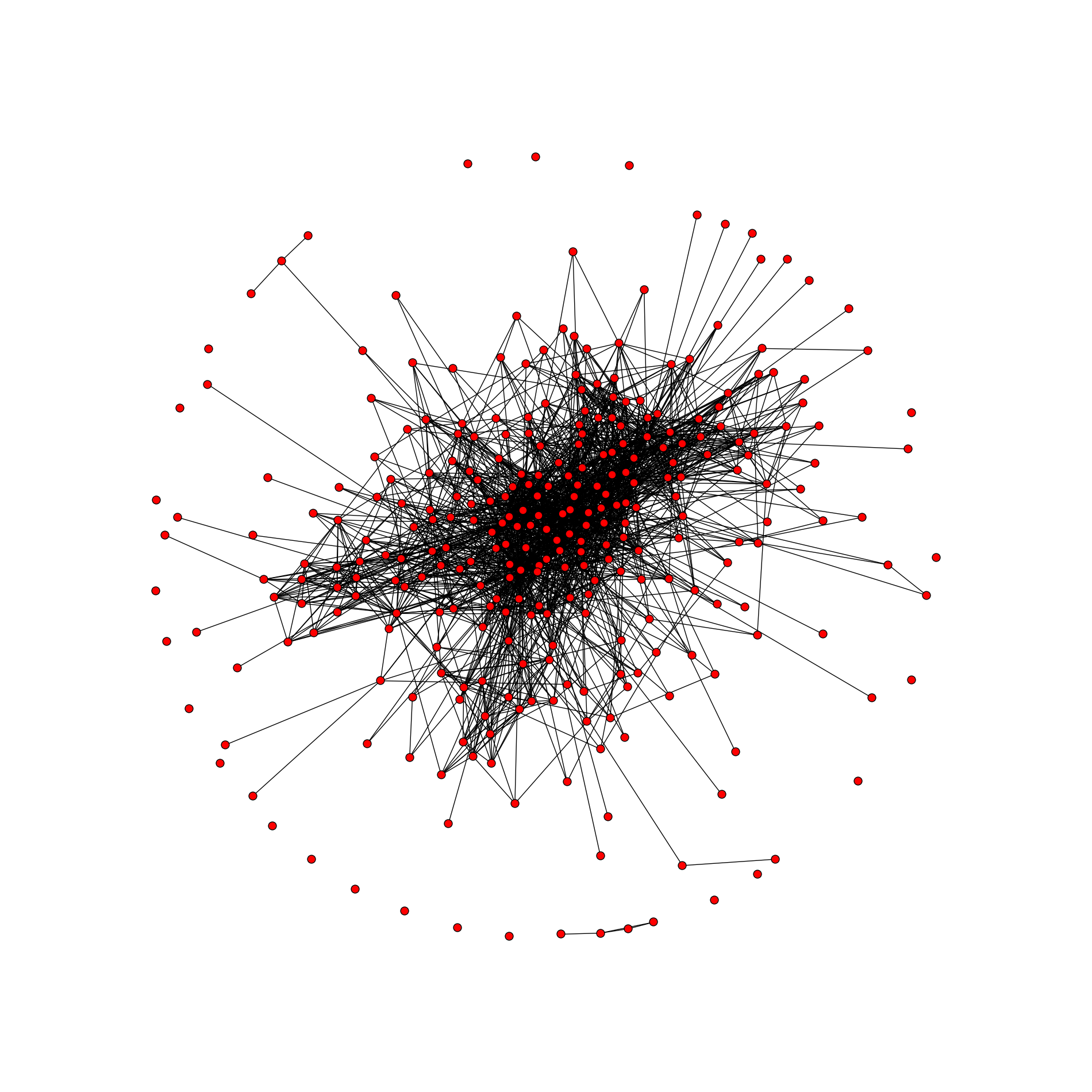
This is a graph of mutual friends, with a total of 306 vertices and 2096 edges. Unfortunately, I have never been a designer (almost all the settings are standard), but you can always stylize the graph “for yourself”. Here are a couple of links:
And the method itself looks like this:
As a result, you get a picture of the date graph.png in the project folder. I do not recommend drawing a graph for deep friends. With 308 friends and a depth of 2, there are more than 145,000 keys in the dictionary. And there are after all also values - tuples with id, which are unlikely to be small.
For a long time I was looking for the most poor friends on VKontakte profile, although it’s more important - friends and friends. There are 10 initial friends (1 of them is locked and will be automatically deleted), with our standard depth (2), in the dictionary there were 1234 keys and 517 174 id (from values). Approximately 419 friends for one id. Yes, there are common friends, when we build a graph, we will understand this:
Will return:
With such big data it would be nice to play around. Networkx has a very large list of algorithms that can be applied to graphs. Let us examine some of them.
First, let's determine if the graph is connected:
A connected graph is a graph in which any pair of vertices is connected by a route.
By the way, at the same id with a depth equal to 1, this is such a beautiful graph containing 1268 vertices and 1329 edges:
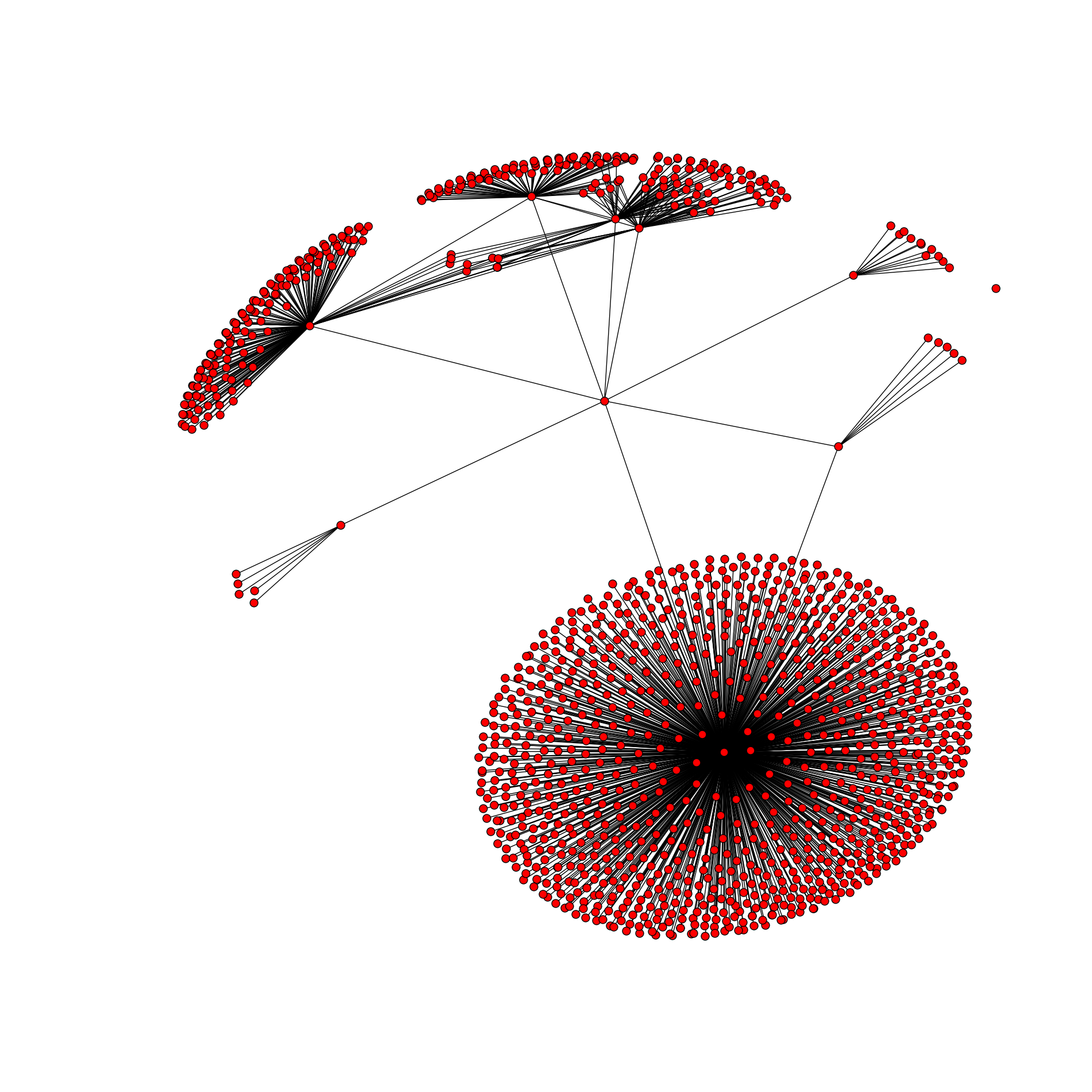
A question for connoisseurs. Once we have a graph of friends of friends, it should be connected anyway. There can not be such that from nowhere a vertex appears that is not connected with any of the existing ones. However, we see on the right one vertex that is not connected to any one. Why? I urge you to think first, it will be more interesting to learn the truth.
We assume that you will not have such a situation, that is, most likely you will see True .
Recall that the diameter of a graph is the maximum distance between its two vertices.
The center of a graph is any vertex, such that the distance from it to the most distant vertex is minimal. The center of the graph can be one vertex or several vertices. Or easier. The center of the graph is a vertex, eccentricity (the distance from this vertex to the farthest from it) is equal to the radius.
Returns a list of vertices that are the center of the graph. Do not be surprised if the center is the id specified in settings.py .
The radius of the graph is the smallest eccentricity of all vertices.
This is the same Page Rank , which you thought. As a rule, the algorithm is used for web pages or other documents linked by links. The more links to a page, the more important it is. But nobody forbids using this algorithm for graphs. We will borrow a more precise and suitable definition from this article :
Quoting Wikipedia:
As you can see, there is nothing complicated, and networkx offers many more algorithms (the author counted 148) that can be applied to graphs. You just have to choose the algorithm you need and call the appropriate method in the graph.py file .
We made a distributed system that allows you to collect and build a graph of common friends on VKontakte, which works 60 times faster (depending on the number of workers) than the proposed version from Himura , also implemented a new function - a request from all "deep friends", added the ability to analyze constructed graphs.
If you do not want to install additional software and you need to build a beautiful graph of mutual friends from the previous article , then the old release is at your service. In it, you will also find the old version of retrieving the list of friends of the user recursively as deeply as you like.
This is not the limit at all, work will continue to increase the speed of the program.
Still waiting for you delicious pull requests, especially if you are engaged in data visualization. Thanks for attention!
To begin with, simply downloading all user id's is easy enough; a list of valid id can be found in the Vkontakte User Catalog . Our task is to get a list of friends of our chosen user id, their friends, and recursively as much as desired, depending on the specified depth.
The code published in the article will change over time, so a more recent version can be found in the same project on Github .
How we will implement:
- We set the depth we need
- We send the source data or the id, which must be investigated at a given depth
- We get the answer
What we will use:
- Python 3.4
- VKontakte stored procedures
We set the depth we need
What we need at the beginning is to indicate the depth ( deep ) with which we want to work. This can be done immediately in settings.py :
')
deep = 2 # deep equal to 1 is our friends, 2 is friends of our friends and so on. As a result, we get a dictionary, the keys of which are the users' id, and the values are their list of friends.
Do not rush to set a large depth. With 14 of my original friends and a depth of 2, the number of keys in the dictionary was 2427, and with a depth of 3, I didn’t have the patience to wait for the script to finish, at that time the dictionary had 223,908 keys. For this reason, we will not visualize such a huge graph, because the vertices are the keys, and the edges are the values.
Sending data
The already known friends.get method, which will be located in a stored procedure that has the following form, will help us achieve the result we need:
var targets = Args.targets; var all_friends = {}; var req; var parametr = ""; var start = 0; // while(start<=targets.length){ if (targets.substr(start, 1) != "," && start != targets.length){ parametr = parametr + targets.substr(start, 1); } else { // , id req = API.friends.get({"user_id":parametr}); if (req) { all_friends = all_friends + [req]; } else { all_friends = all_friends + [0]; } parametr = ""; } start = start + 1; } return all_friends; I remind you that you can create a stored procedure in the application settings , it is written in VkScript , as well as execute , the documentation can be read here and here .
Now how it works. We accept a string of 25 id, separated by commas, take out one id, make a request to friends.get , and the information we need will come in the dictionary, where the keys are id, and the values are a list of friends of this id.
When you first start, we will send to the stored procedure a list of friends of the current user whose id is specified in the settings. The list will be divided into several parts (N / 25 - this is also the number of requests), this is due to the limitation of the number of calls to the VKontakte API.
Getting an answer
We store all received information in a dictionary, for example:
{1:(0, 2, 3, 4), 2: (0, 1, 3, 4), 3: (0, 1, 2)} The keys 1, 2 and 3 were obtained with a depth equal to 1. Suppose that these were all the friends of the specified user (0).
If the depth is greater than 1, then we use the difference of sets, the first of which is the dictionary values, and the second is its keys. Thus, we get those id (in this case, 0 and 4), which are not in the keys, divide them again into 25 parts and send to the stored procedure.
Then in our dictionary there will be 2 new keys:
{1:(0, 2, 3, 4), 2: (0, 1, 3, 4), 3: (0, 1, 2), 0: (1, 2, 3), 4:(1, 2, ….)} The very method deep_friends () looks like this:
def deep_friends(self, deep): result = {} def fill_result(friends): for i in VkFriends.parts(friends): r = requests.get(self.request_url('execute.deepFriends', 'targets=%s' % VkFriends.make_targets(i))).json()['response'] for x, id in enumerate(i): result[id] = tuple(r[x]["items"]) if r[x] else None for i in range(deep): if result: # , + id:None fill_result(list(set([item for sublist in result.values() if sublist for item in sublist]) - set(result.keys()))) else: fill_result(requests.get(self.request_url('friends.get', 'user_id=%s' % self.my_id)).json()['response']["items"]) return result Of course, this is faster than throwing one id at friends.get without using a stored procedure, but it still takes a lot of time.
If friends.get were similar to users.get , namely, it could take user_ids as a parameter, that is, id listed by comma, for which you need to return a list of friends, rather than one id, then the code would be much simpler, and The number of requests was several times less.
Too slow
Returning to the beginning of the article, I can repeat it again - very slowly. Stored procedures do not save, the alxpy solution with multithreading (thanks to him for his contribution and participation
Wise advice received from igrishaev - we need some kind of map.
The fact is that VKontakte resolves 25 requests to the API through execute , it follows from this that if we make requests from different clients, we can increase the number of valid requests. 5 wheelbarrows - this is 125 requests per second. But this is far from the case. Looking ahead, I will say that it is possible and even faster, it will look something like this (on each machine):
while True: r = requests.get(request_url('execute.getMutual','source=%s&targets=%s' % (my_id, make_targets(lst)),access_token=True)).json() if 'response' in r: r = r["response"] break else: time.sleep(delay) If we receive an error message, we make a request again, after a specified number of seconds. This technique works for some time, but then VKontakte starts to send None in all answers, so after each request we honestly wait for 1 second. For now.
Next, we need to choose new tools or write our own to realize our plans. As a result, we should have a horizontally scalable system, the principle of operation seems to me as follows:
- The main server receives from the client its VK id and operation code: either pull out all mutual friends, or walk recursively through the list of friends with the specified depth.
- Further, in both cases, the server makes a request to the VK API - we need a list of all the user's friends.
- Since everything is done so that we use the maximum capabilities of the stored procedures - here it will be necessary to divide the list of friends into parts, 25 contacts each. In fact, 75. More on this below.
- We will have many parts, using the message broker, we will deliver each part to a specific recipient (producer-consumer).
- Recipients will accept contacts, immediately make requests, return the result to the supplier. Yes, you thought correctly about RPC.
And if you saw this picture, then you understand what message broker I am hinting at.

Once all the answers are accepted, we merge them into one. Further, the result can be displayed on the screen or even saved, more on that later.
Here it is worth noting that the code will change, and if it was enough for you to use the previous version of the project, then it remained unchanged. All the code below will be for the new release.
As a message broker, we will use RabbitMQ , an asynchronous distributed job queue - Celery .
For those who have never come across them, here are some useful links to materials that I advise you to read:
Celery
Do not be afraid to understand, although they say that you can specifically turn your head when you start to “think not with one computer, but with several”, but this is not at all the case.
If you have a Mac, like the author, then RabbitMQ is smartly installed via Homebrew :
brew update brew install rabbitmq Celery is put even easier, we use the third branch of Python :
pip3 install Celery I have Celery installed on Linux Mint, and RabbitMQ on Mac. With Windows, as usual, the problems are
Next, create a virtual host , user, and give him the right:
rabbitmqctl add_vhost vk_friends rabbitmqctl add_user user password rabbitmqctl set_permissions -p vk_friends user ".*" ".*" ".*" In the RabbitMQ configuration, you must specify the ip of the host on which it is installed:
vim /usr/local/etc/rabbitmq/rabbitmq-env.conf NODE_IP_ADDRESS=192.168.1.14 // Here are some possible configurations, which one to choose is up to you.

If you have a router or something else, it will be useful to know that RabbitMQ uses port 5672, well, and make redirection in the settings of your device. Most likely, if you test, you scatter the workers on different machines, and they will need to use a broker, and if you don’t correctly set up the network, Celery will not reach RabbitMQ .
Very good news is that VKontakte allows you to do 3 requests per second from one id. Multiply these requests by the number of possible calls to the VKontakte API (25), we get the maximum number of contacts processed per second (75).

If we have a lot of workers, then the moment will come when we begin to go beyond the allowed limit. Therefore, the token variable (in settings.py ) will now be a tuple containing several tokens from different id. At each request to the VK API, the script will choose one of them in a random way:
def request_url(method_name, parameters, access_token=False): """read https://vk.com/dev/api_requests""" req_url = 'https://api.vk.com/method/{method_name}?{parameters}&v={api_v}'.format( method_name=method_name, api_v=api_v, parameters=parameters) if access_token: req_url = '{}&access_token={token}'.format(req_url, token=random.choice(token)) return req_url In this regard, you should have no difficulties if there are several accounts on VKontakte (you can strain friends, relatives), I did not have problems with 4 tokens and 3 workers.
No, no one bothers you to use time.sleep () , or the example above with while, but then get ready to receive error messages (empty answers are possible at all - id: None), or wait a little longer.
The most interesting from the file call.py :
def getMutual(): all_friends = friends(my_id) c_friends = group(mutual_friends.s(i) for i in parts(list(all_friends[0].keys()), 75))().get() result = {k: v for d in c_friends for k, v in d.items()} return cleaner(result) def getDeep(): result = {} for i in range(deep): if result: # , + id:None lst = list(set([item for sublist in result.values() if sublist for item in sublist]) - set(result.keys())) d_friends = group(deep_friends.s(i) for i in parts(list(lst), 75))().get() result = {k: v for d in d_friends for k, v in d.items()} result.update(result) else: all_friends = friends(my_id) d_friends = group(deep_friends.s(i) for i in parts(list(all_friends[0].keys()), 75) )().get() result = {k: v for d in d_friends for k, v in d.items()} result.update(result) return cleaner(result) As you can see, in 2 functions we use groups () , which runs several tasks in parallel, after which we “glue” the answer. Remember how deep_friends () looked at the beginning (there’s a very old example - even without multithreading)? The meaning remains the same - we use the set difference.
And finally, tasks.py . Someday these great features will merge into one:
@app.task def mutual_friends(lst): """ read https://vk.com/dev/friends.getMutual and read https://vk.com/dev/execute """ result = {} for i in list(parts(lst, 25)): r = requests.get(request_url('execute.getMutual', 'source=%s&targets=%s' % (my_id, make_targets(i)), access_token=True)).json()['response'] for x, vk_id in enumerate(i): result[vk_id] = tuple(i for i in r[x]) if r[x] else None return result @app.task def deep_friends(friends): result = {} for i in list(parts(friends, 25)): r = requests.get(request_url('execute.deepFriends', 'targets=%s' % make_targets(i), access_token=True)).json()["response"] for x, vk_id in enumerate(i): result[vk_id] = tuple(r[x]["items"]) if r[x] else None return result When everything is set up, run RabbitMQ with the command:
rabbitmq-server Then go to the project folder and activate the worker:
celery -A tasks worker --loglevel=info Now, to get and save a list of common or "deep" friends, just command in the console:
python3 call.py About measurement results
Let me remind you that the author of the article , which inspired me to the first part , had 343 friends (a request for mutual friends) “processed” in 119 seconds .
My version of the previous article did the same thing in 9 seconds .
Now that author has a different number of friends - 308. Well, you have to make one extra request for the last eight id, spend a precious second on it, although you can process 75 id in that second.
With one worker, the script took 4.2 seconds , and with two workers, 2.2 seconds .
If 119 is round to 120, and 2.2 to 2, then my version works 60 times faster .
As for the “deep friends” (friends of my friends and so on + we test on another id to wait less) - with a depth equal to 2, the number of keys in the dictionary was 1,251.
The execution time of the code given at the very beginning of the article is 17.9 seconds .
With one worker, the script execution time is 15.1 seconds , with two workers, 8.2 seconds .
Thus, deep_friends () has become about 2.18 times faster.
Yes, the result is not always so bright, sometimes you have to wait 10 or 20 seconds for a response to one VKontakte (although the frequent execution time of one task is 1.2 - 1.6 seconds ), most likely, this is due to the load on the service, because we not alone in the universe.

As a result, the more workers do, the faster the result will be processed. Do not forget about the power of your hardware, additional tokens, the network (for example, the author dramatically increased the script execution time when he used his iPhone as an access point) and other factors.
Saving result
Yes, there are a lot of graph-oriented databases. If in the future (and it will be so), we want to analyze the results obtained, then all the same they will need to be stored somewhere until the analysis itself, then the same results should be uploaded to the memory and some actions should be taken with them. I see no reason to use any subd, if the project would be commercial and we were interested in, for example, what happens to the graph of a particular user over time - then yes, then the graph-oriented database is obligatory, but since we will be engaged in the analysis at home “ Pickle is enough for us.
Before saving dictionaries, it will be logical to delete from them keys whose values are None . These are blocked or deleted accounts. Simply put, these id will be in the column, because they have someone as friends, well, we will save on the number of keys in the dictionary:
def cleaner(dct): return {k:v for k, v in dct.items() if v != None} def save_or_load(myfile, sv, smth=None): if sv and smth: pickle.dump(smth, open(myfile, "wb")) else: return pickle.load(open(myfile, "rb")) As you can see, if we save the result somewhere, then we need to load it somewhere in order not to collect the id again.
Graph analysis
In order not to write your bike, let's use a fairly well-known networkx , which will do all the
pip3 install networkx Before we begin to analyze the graph, draw it. networkx for this you need matplotlib :
pip3 install matplotlib Next we need to create the graph itself. In general, there are 2 ways.
The first will eat a lot of RAM and your time:
def adder(self, node): if node not in self.graph.nodes(): self.graph.add_node(node) self.graph = nx.Graph() for k, v in self.dct.items(): self.adder(k) for i in v: self.adder(i) self.graph.add_edge(k, i) And this is not the author has survived the mind, no. A similar example is given on the Rice University page , under the heading Convert Dictionary Graph Representation into networkx Graph Representation :
def dict2nx(aDictGraph): """ Converts the given dictionary representation of a graph, aDictGraph, into a networkx DiGraph (directed graph) representation. aDictGraph is a dictionary that maps nodes to its neighbors (successors): {node:[nodes]} A DiGraph object is returned. """ g = nx.DiGraph() for node, neighbors in aDictGraph.items(): g.add_node(node) # in case there are nodes with no edges for neighbor in neighbors: g.add_edge(node, neighbor) return g You can take my word for it, the count was being built the whole evening, when there were already more than 300,000 peaks in it, my patience snapped.
Yes, an example is given for a directed graph, but the essence remains the same - first we add keys, making them vertices, then making vertices of the values, and then if they are not already in the graph, and then we connect them with edges (in my version).
And the second method will do everything in seconds:
self.graph = nx.from_dict_of_lists(self.dct) The code lies in the graph.py file, to draw a graph of mutual friends, just run this script or create an instance of the VkGraph () class somewhere and then call its draw_graph () method.

This is a graph of mutual friends, with a total of 306 vertices and 2096 edges. Unfortunately, I have never been a designer (almost all the settings are standard), but you can always stylize the graph “for yourself”. Here are a couple of links:
And the method itself looks like this:
def draw_graph(self): plt.figure(figsize=(19,19), dpi=450,) nx.draw(self.graph, node_size=100, cmap=True) plt.savefig("%s graph.png" % datetime.now().strftime('%H:%M:%S %d-%m-%Y')) As a result, you get a picture of the date graph.png in the project folder. I do not recommend drawing a graph for deep friends. With 308 friends and a depth of 2, there are more than 145,000 keys in the dictionary. And there are after all also values - tuples with id, which are unlikely to be small.
For a long time I was looking for the most poor friends on VKontakte profile, although it’s more important - friends and friends. There are 10 initial friends (1 of them is locked and will be automatically deleted), with our standard depth (2), in the dictionary there were 1234 keys and 517 174 id (from values). Approximately 419 friends for one id. Yes, there are common friends, when we build a graph, we will understand this:
deep_friends = VkGraph(d_friends_dct) print(' :', deep_friends.graph.number_of_nodes()) print(' :', deep_friends.graph.number_of_edges()) Will return:
: 370341 : 512949 With such big data it would be nice to play around. Networkx has a very large list of algorithms that can be applied to graphs. Let us examine some of them.
Connected graph
First, let's determine if the graph is connected:
print(' ?', nx.is_connected(deep_friends.graph)) A connected graph is a graph in which any pair of vertices is connected by a route.
By the way, at the same id with a depth equal to 1, this is such a beautiful graph containing 1268 vertices and 1329 edges:

A question for connoisseurs. Once we have a graph of friends of friends, it should be connected anyway. There can not be such that from nowhere a vertex appears that is not connected with any of the existing ones. However, we see on the right one vertex that is not connected to any one. Why? I urge you to think first, it will be more interesting to learn the truth.
Correct answer
Let's see. First, a list of friends is taken, and it turns out that we have id X. Because of which the graph is incoherent. Next, we make a request to the friends of this X (in depth because). So if X has all the friends hidden, then there will be an entry in the dictionary:
When the graph is built, we honestly add the vertex X, but it will not have any edges. Yes, theoretically, the vertex X should have an edge with a vertex whose id is specified in settings.py , but you read it carefully - we add only what is in the dictionary. Therefore, with a depth equal to 2, we will get the id specified in the settings in the dictionary. And then edges will appear at vertex X.
{X:(), ...} When the graph is built, we honestly add the vertex X, but it will not have any edges. Yes, theoretically, the vertex X should have an edge with a vertex whose id is specified in settings.py , but you read it carefully - we add only what is in the dictionary. Therefore, with a depth equal to 2, we will get the id specified in the settings in the dictionary. And then edges will appear at vertex X.
We assume that you will not have such a situation, that is, most likely you will see True .
Diameter, center and radius
Recall that the diameter of a graph is the maximum distance between its two vertices.
print(' :', nx.diameter(deep_friends.graph)) The center of a graph is any vertex, such that the distance from it to the most distant vertex is minimal. The center of the graph can be one vertex or several vertices. Or easier. The center of the graph is a vertex, eccentricity (the distance from this vertex to the farthest from it) is equal to the radius.
print(' :', nx.center(deep_friends.graph)) Returns a list of vertices that are the center of the graph. Do not be surprised if the center is the id specified in settings.py .
The radius of the graph is the smallest eccentricity of all vertices.
print(' :', nx.radius(deep_friends.graph)) Authority or page rank
This is the same Page Rank , which you thought. As a rule, the algorithm is used for web pages or other documents linked by links. The more links to a page, the more important it is. But nobody forbids using this algorithm for graphs. We will borrow a more precise and suitable definition from this article :
Authority in the social graph can be analyzed in various ways. The easiest one is to sort the participants by the number of incoming edges. Who has more - the more authoritative. This method is suitable for small graphs. Searching on the Internet, Google uses PageRank as one of the criteria for authoritative pages.It is calculated using a random walk along the graph, where the nodes are the pages and the edge between the nodes is if one page refers to another. The random walker moves along the graph and from time to time moves to a random node and starts the walk again. PageRank is equal to the proportion of stay on a node for the entire time of wandering. The more it is, the more authoritative the node.
import operator print('Page Rank:', sorted(nx.pagerank(deep_friends.graph).items(), key=operator.itemgetter(1), reverse=True)) Clustering coefficient
Quoting Wikipedia:
The clustering factor is the degree of probability that two different users associated with a particular individual are also connected.
print(' ', nx.average_clustering(deep_friends.graph)) As you can see, there is nothing complicated, and networkx offers many more algorithms (the author counted 148) that can be applied to graphs. You just have to choose the algorithm you need and call the appropriate method in the graph.py file .
Total
We made a distributed system that allows you to collect and build a graph of common friends on VKontakte, which works 60 times faster (depending on the number of workers) than the proposed version from Himura , also implemented a new function - a request from all "deep friends", added the ability to analyze constructed graphs.
If you do not want to install additional software and you need to build a beautiful graph of mutual friends from the previous article , then the old release is at your service. In it, you will also find the old version of retrieving the list of friends of the user recursively as deeply as you like.
This is not the limit at all, work will continue to increase the speed of the program.
Still waiting for you delicious pull requests, especially if you are engaged in data visualization. Thanks for attention!
Source: https://habr.com/ru/post/243229/
All Articles