Why Spritz has become so popular over the past few weeks.

Hello, dear cryptographers and mathematicians!

It is difficult for me, not professional mathematics and not a cryptographer, to understand immediately how the encryption algorithm works. Before you try to deal with the individual functions of a single algorithm. And also, to understand why the Spritz algorithm is now more discussed by experts than, for example, Keccak . On Habré there were several articles that described the Sponge function , or, in Russian, the sponge ( one , two ). This function can be used in several ways: as a cryptor / decryptor, as a hash, as a hash with separate domains, to form a message authenticity code (MAC) or simulator, to work as a stream cipher and as a stream cipher with random access, for authentication with associated data (Authenticated Encryption with Associated Data) as a pseudo-random number generator and for generating symmetric keys from passwords.

To figure it out, I used the original article and presentation , as well as the source code from GitHub ( C , JS ).

Since I am not an expert, I’ll start with examples. In particular, from the function hash (M, r).
')
M is the input byte array.
r is the length of the output hash of the array in bytes.

As can be seen from the example, the input array has a length of 3 bytes, and the output is 32 bytes. Thus, the array length is increased by 29 bytes.

Let's see how this happens.

Initially, the variables and the array of permutations are initialized.

i = j = k = z = a = 0;
w = 1;

i, j are the positions of two elements.
to - key
z is the last calculated value.
a - the number of used nibbles (nibbles)

All of these values ​​are initially zero. And the array of permutations initially has ordered values ​​from 1 to N. In our example, N is 256.

w - the width of the hop is 1, but may vary depending on the presence of the greatest common factor with N.

Soak up

Then the function is called absorb (M) - absorption, as we remember the array M in the example consists of 3 bytes. For definiteness, let it be bytes 'A', 'B' and 'C'. The “sponge” has a rather large size of 256 bytes, for our 3 bytes that need to be absorbed. For each byte, we call the function absorbByte ('A'), similarly for 'B' and 'C'.

Each byte is divided into two nibbla - the older and the younger, and for each of them we call the function absorbNibble ('low 4 bits'), the same for the high 4 bits of a byte.
How does the current nibbla absorb? The function absorbNibble takes the first byte from the array of permutations (it is equal to 1) and interferes with its position equal to the middle of the array
permutations plus the value of the nibbl itself. Since code A is equal to 65. Then the lowest nibble is 1, then the new position for the first element is 128 + 1 = 129.
And in the first position we will have the number 129.

Next, we increase the count of used nibls by 1 (a = 2).

We do the same for the older nibbl and for the remaining 2 bytes. In total, in our example, 6 permutations should be carried out, according to the number of nibbles used.

Shack

After that, run the function shuffle () - shuffle.

Here's what she looks like:

/* Shuffle() 1 Whip(2N) 2 Crush() 3 Whip(2N) 4 Crush() 5 Whip(2N) 6 a=0 */ function shuffle() { whip(TWO_N); crush(); whip(TWO_N); crush(); whip(TWO_N); a = 0; } 

The first thing to do is run the update () function - update 2N times. It is in this function that Spritz differs from RC4 ( presentation , analysis ).

Compare operations with RC4

RC4:

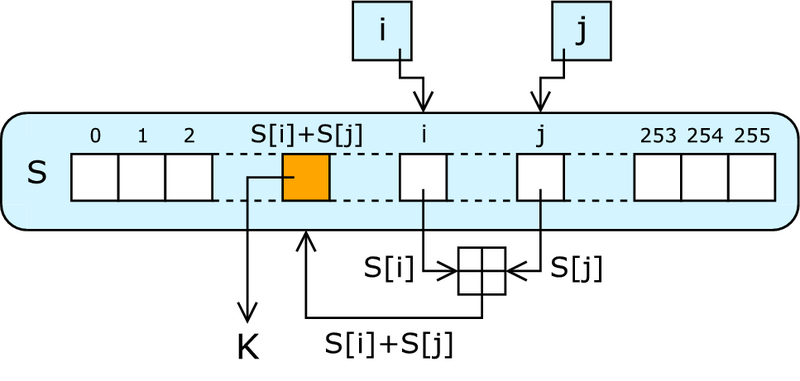
 1: i = i + 1 2: j = j + S[i] 3: SWAP(S[i];S[j]) 4: z = S[S[i] + S[j]] 5: Return z 

Spritz:

 1: i = i + w 2: j = k + S[j + S[i]] 2a: k = i + k + S[j] 3: SWAP(S[i];S[j]) 4: z = S[j + S[i + S[z + k]]] 5: Return z 

Spritz with my modification for better understanding:

 1: i = i + w 2: j = j + S[i] 2a: j = k + S[j] 2b: k = i + j 3: SWAP(S[i];S[j]) 4a: i = i + S[k+z] // z=S[j] c   4b: j = j + S[i] 4c: z = S[j] 5: Return z 

4, the operation can be represented as: Ez = S [j + S [i + S [k + z]]] = kzpSipSjpS.

Shake and crush

The parameter w appeared - which must be an odd number. In RC4, it is always 1.
Another dependent parameter, k, has appeared.
The function name Whip (2N) can be translated as shaking, and Crush () as pressure.

The Whip function performs operations 1,2,2a, 3. Then it increases the parameter w by one as many times as the largest common factor for w and N will be found.

i runs through all values ​​from 1 to 512. Suppose that k = 0. So it is set during initialization. Then, before the first iteration, j will be equal to 0. And after the first iteration, j = S [S [1]], but S [1] = 129, and if, with absorb, the first and 129 elements were rearranged only once, then j = 1. Then k at step 2a will take the value k = 129.

The Crush () function changes the values ​​symmetric about the center of the array of permutations if the value on the right side is greater than the value on the left side.

Squeeze

This is the final operation squeeze (r). In our output array \ hash, we need to get r bytes. After calling drip () and update (), the final output () operation is performed:

  /* Output() 1 z = S[j+S[i+S[z+k]]] 2 return z */ function output() { z = S[ madd(j, S[ madd(i, S[ madd(z, k) ]) ]) ]; return z; } 

As you can see, unlike RC4, this operation depends on the value of z calculated at the previous step. It turns out several fractal algorithm.

Notice

This is a completely new cipher, it will take time before this analysis appears. As a result of viewing the code, I drew on the following features.

  /* addition modulo N */ function madd(a, b) { return (a + b) % N; // return (a + b) & 0xff; // when N = 256, 0xff = N - 1 } /* subtraction modulo N. assumes a and b are in N-value range */ function msub(a, b) { return madd(N, a - b); } 

All summation and subtraction are done on a cyclic buffer with size N (this is specified in the article). This is probably a feature of this particular implementation, but it seemed to me that in some it is a rather simple summation or difference. If I understand correctly, the size of the buffer may be different.

The code is sensitive to the initial value of w. During initialization, this parameter is set to 1. What happens if it is set to N?

The array of permutations S is initialized with values ​​from 1 to N, therefore S [i] = i, if the input buffer length is small, then this will be true in subsequent rounds.

With a special selection of the key and the initialization vector (IV), it is possible that some operations will be greatly simplified. And they will have low algebraic complexity in general. For example, 2a may be equivalent to j = k + (i + j) << 1.

Total

A very interesting approach to encryption is developed in Spritz. In my opinion, existing implementations require significant refinement. Also, it will take time before this strong cipher becomes clear or not. It is already clear that it is slower than RC4. This cipher is laid out in open access and does not have any license restrictions.

Probably, Spritz can become popular as it has the following Sponge functions: AbsorbStop function, Encryption, Hash function, Domain separation hash function, Authentication Encryption with Associated Data (AEAD), Deterministic Random Bit Generator (DRBG) ).

Perhaps these functions can be used for distributed databases, for transferring audio and video over the Internet, etc.

Also, if respected specialists would like it, I can write the following article, where I will show how to use AEAD to make a one-time digital key that works only for a certain time. This can be used, in particular, for remote leasing of a car, motel, yacht or apartment or for managing IoT facilities in a hotel or guest house.

PS Thanks Ivan_83 for the link. Low algebraic complexity Keccak / Keyak facilitates cubic attacks.