Persistent Cartesian tree by implicit key

Caution persistence

Today is a rather unusual day, isn't it? How often do articles about persistent data structures appear on Habré? And today I want to tell you about an undeservedly forgotten persistent deramid with an implicit key. So, let's begin.

1. What does the author mean by persistence?

According to the source of knowledge , a persistent data structure is a data structure that stores information about all its previous versions, when its changes were performed.
There are several options for how to make the data structure persistent. In this case, we will create a fully persistent data structure by copying only those vertices in which something has changed. Thus, we don’t need to somehow change the structure of the usual Deramids or completely copy the entire tree with some kind of change. Good? Of course!

2. How to do it?

Consider the usual structure of deramids with an implicit key. In order not to be unfounded, we will consider the amount on the segment.

struct PersistentTreap { int size; long long sum, key; PersistentTreap *left, *right; //     PersistentTreap() { left = NULL; right = NULL; key = sum = 0; size = 0; } PersistentTreap(int x) { left = right = NULL; sum = key = x; size = 1; link = 0; } //      }; typedef PersistentTreap* PtrPersistentTreap; int getSize(PtrPersistentTreap root) { if (!root) return 0; return root->size; } long long getSum(PtrPersistentTreap root) { if (!root) return 0; return root->sum; } void addLink(PtrPersistentTreap root) { if (!root) return; root->link++; } void update(PtrPersistentTreap root) { if (!root) return; root->size = 1 + getSize(root->left) + getSize(root->right); root->sum = root->key + getSum(root->left) + getSum(root->right); } 

As you can see, this is a rather trivial part of the code, which is known to everyone who has ever written a deramid with an implicit key. We now turn to the most interesting: how to make the operations split, merge and push (as an option) not change the tree structure irreversibly?
Consider a few pictures that will help us figure it out.
The original Cartesian tree before the split operation. (the vertices indicate the numbers that correspond to them in the array). That is, it is similar to an array .

')
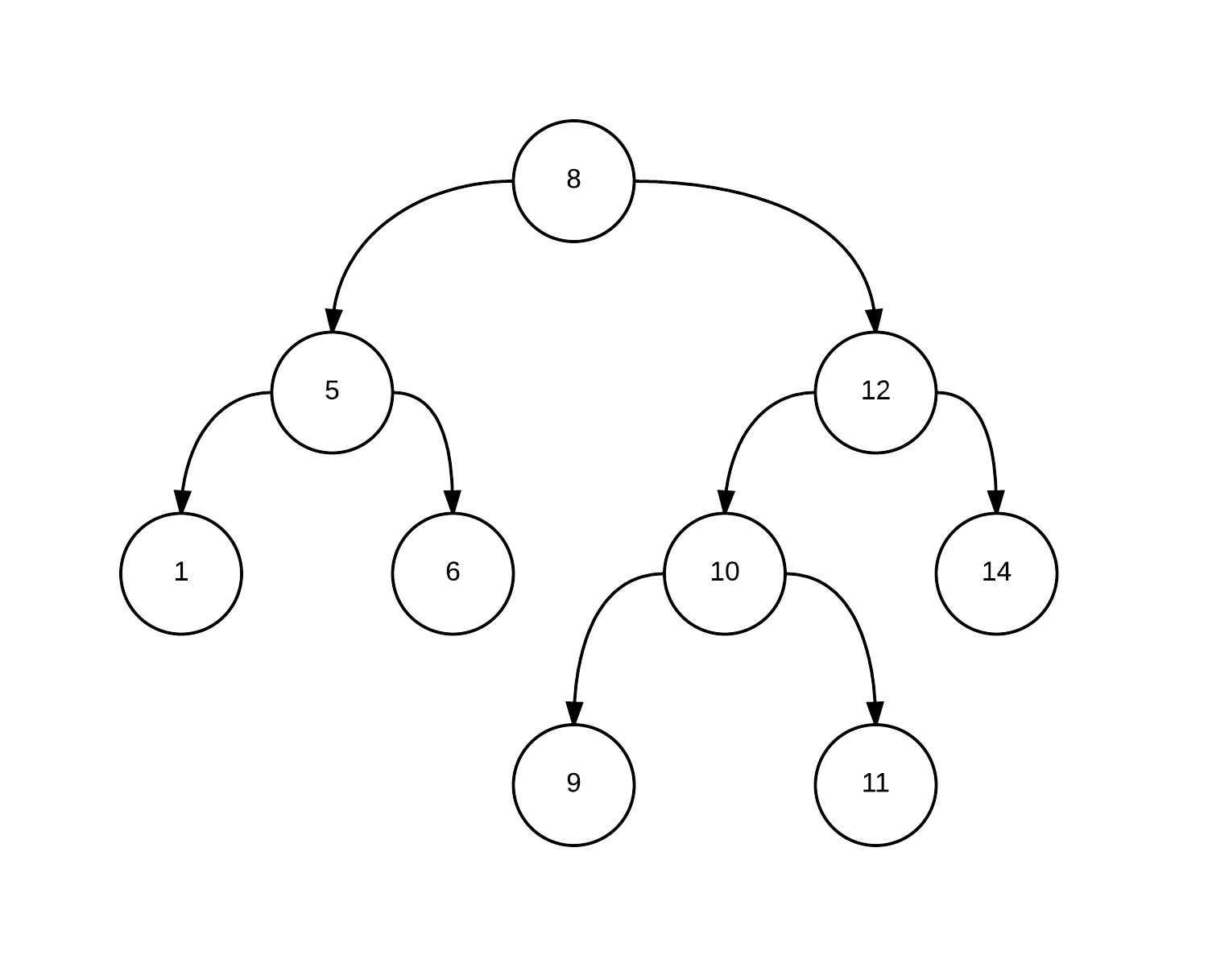
After the persistent split operation, in which we requested 5 elements in the right tree, we get the next forest. Blue marks the vertices of the original Deramids, green marks the newly created vertices. Dotted arrows - connections between new vertices.


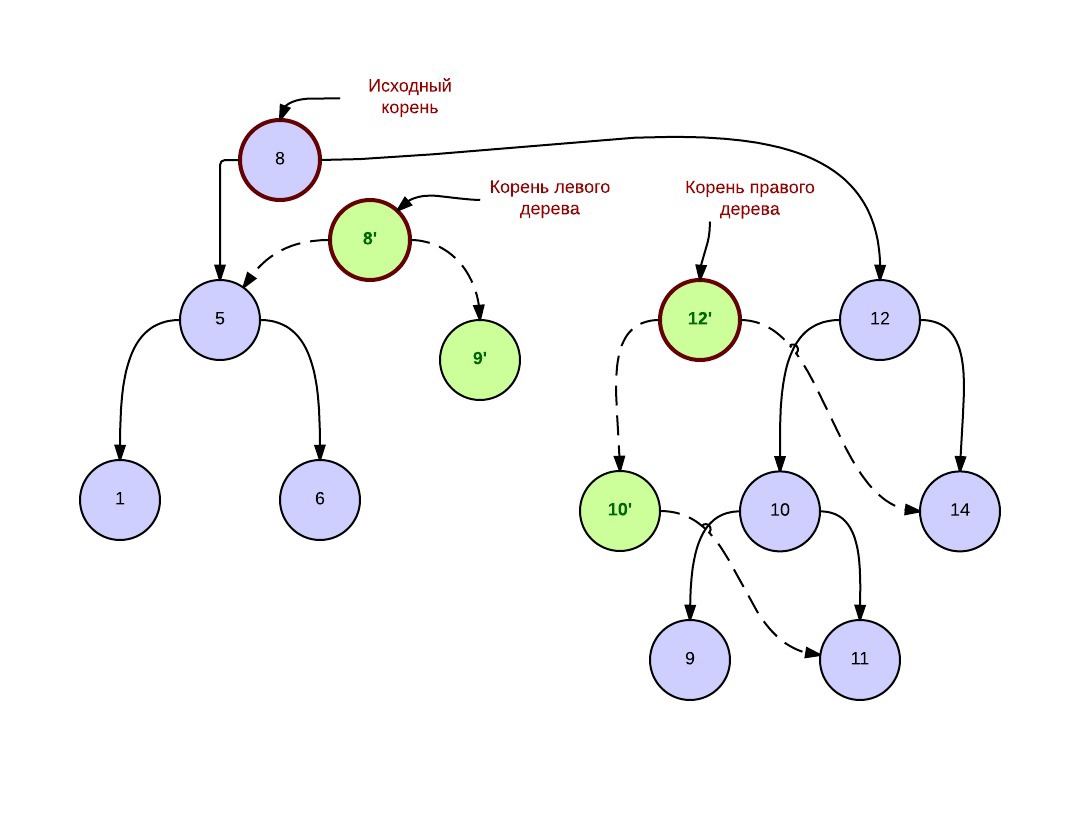
So, with each recursive call of the split operation, we have no right to modify the existing tree in any way, we need to create a new vertex, which is exactly a copy of this and carry out all the changes only with it. Literally we will write this. To do this, we first create a copy constructor:

 PersistentTreap(PersistentTreap* cur) { if (!cur) { return; } left = cur->left; right = cur->right; sum = cur->sum; key = cur->key; size = cur->size; } 

Everything, now you can write the persistent version of the split operation. Its only difference with the usual one is that we simply copy the root that needs to be changed, and continue to do our usual work.

 void Split(PtrPersistentTreap root, PtrPersistentTreap &L, PtrPersistentTreap &R, int size) { if (!root) { L = R = NULL; return; } PtrPersistentTreap cur = new PersistentTreap(root); if (getSize(cur->left) + 1 <= size) { split(cur->right, cur->right, R, size - getSize(cur->left) - 1); L = cur; } else { split(cur->left, L, cur->left, size); R = cur; } update(L); update(R); } 

Great, a third of all the work done. Now you need to deal with the persistent operation merge. Consider the two deramids that were obtained in some way (again, we assume that everything is derived from the original array). For the merge operation to work correctly, assign priorities to them so that the maximum is at the root (highlighted in red in parentheses). Later it will be shown that they are not really needed for the correct operation of the algorithm.


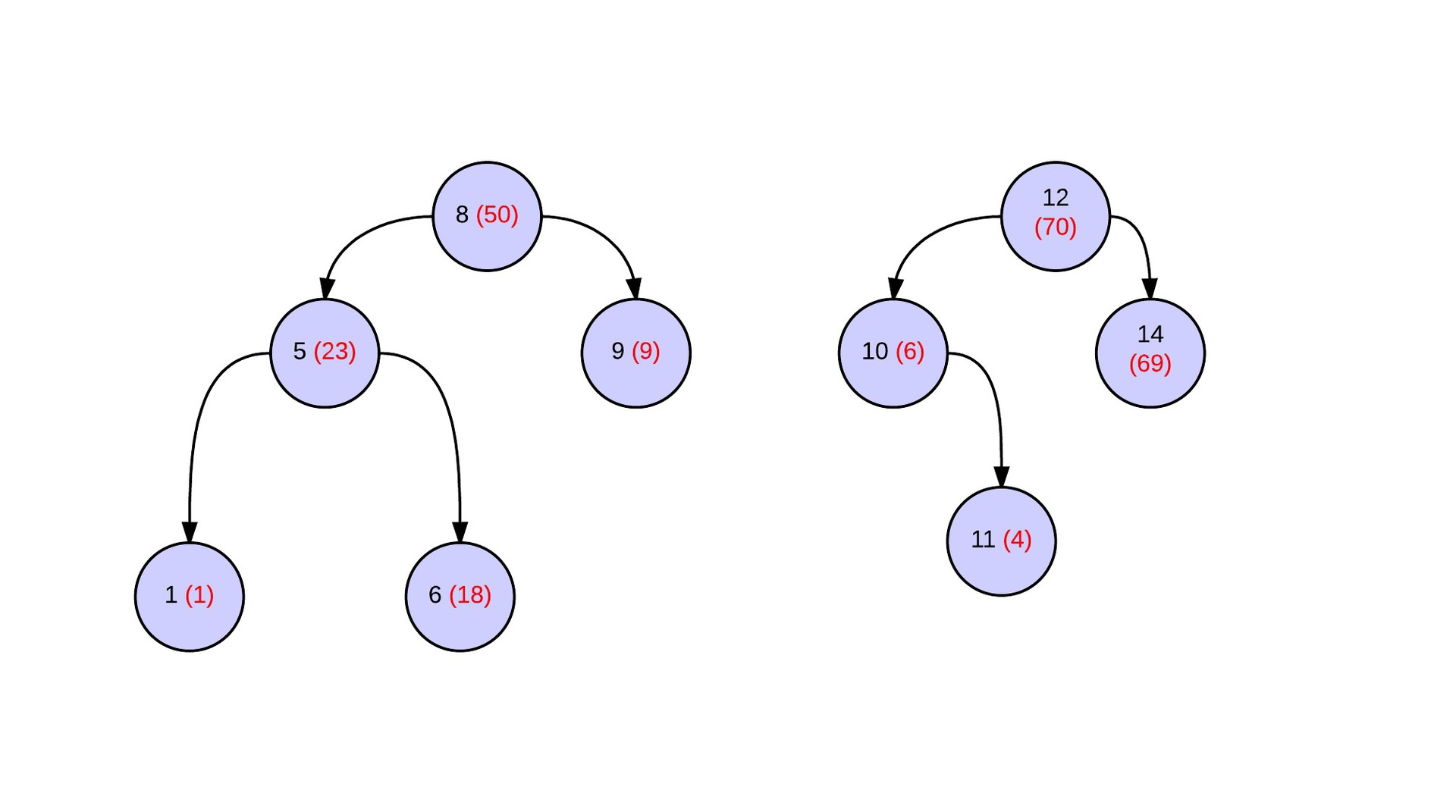
The result of the merge operation is a deramid, in which heap properties are executed for the vertex priorities. Below is a picture of the tree after the operation merge. Blue marks the vertices of the original Deramids, green marks the newly created vertices. Dotted arrows - connections between new vertices.

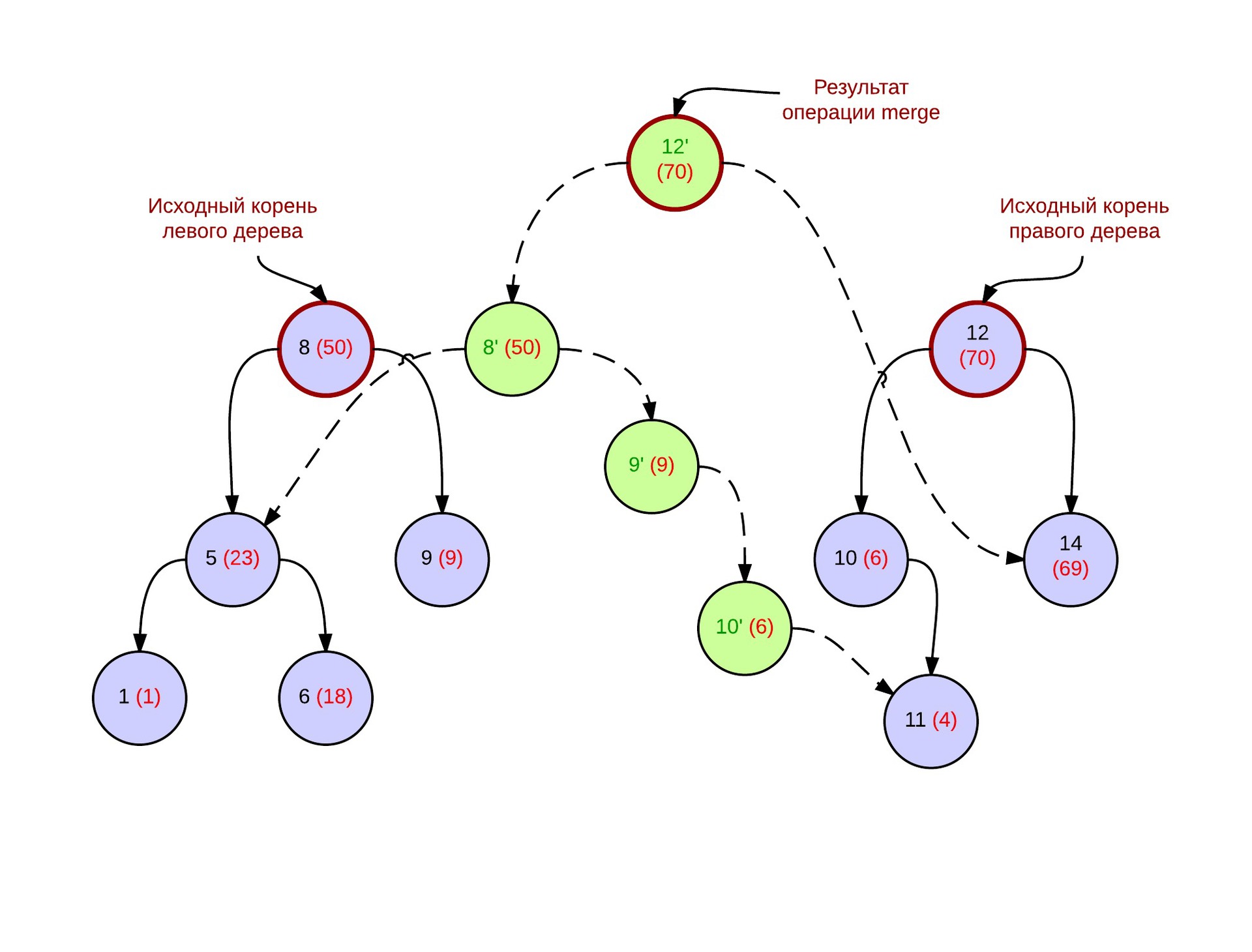
In our implementation, we will require merge to return a pointer to a new top of the tree. Thus, on each call, we copy the vertex that will become the root, and change its pointer to one of her sons. On which - depends on whether it was a left or right tree.

 PtrPersistentTreap Merge(PtrPersistentTreap L, PtrPersistentTreap R) { PtrPersistentTreap ptrNode = NULL; if (!L || !R) { ptrNode = new PersistentTreap((!L ? R : L)); return ptrNode; } if (L->prior > R->prior) { ptrNode = new PersistentTreap(L); ptrNode->right = Merge(L->right, R); update(ptrNode); return ptrNode; } else { ptrNode = new PersistentTreap(R); ptrNode->left = Merge(L, R->left); return ptrNode; } } 

However, it was promised that at the vertices there is absolutely no need to store the whole field prior, now I will tell you how to get rid of it (it is extremely useful for persistent implementation). Indeed, if the priorities coincide, the tree can degenerate into ordinary bamboo, which reduces its benefit immediately to nothing. To expose a new priority at each call to the top is expensive, not the fact that it does not exactly coincide with any other, nor the fact that the tree structure will remain. It turns out there is a simple and elegant solution.

Each vertex of the deramids stores in the size of the tree it represents. So with this value, you can try to associate the priority of the vertex to become a root. It is logical enough to make the priority of the top, which has a larger tree size, was larger. We now prove that in this case each vertex has the same probability of becoming the root of the tree. We do this by induction. Suppose we want to choose a root of two vertices. Obviously, the probabilities of becoming the root for them are equal. Now consider the case when we have all L vertices in the left tree, and R. in the right tree. Then, according to the algorithm, a vertex from the left tree can become a root with probability 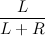. But each vertex of a tree L could become a root with the probability . So each vertex of a tree L can become a root with probability . Similarly, the case for the right tree is considered. Everything, the transition is proved, since the probabilities for all vertices are the same.
So in operation merge instead of

 if (L->prior > R->prior) 

can write

 int l = getSize(L), r = getSize(R), rang = rand() % (l + r); if (rang > r) 

and nothing will change.

3. Add counting links to the top.

Hurray, the main part of the persistent data structure is written. The following changes that need to be made are the implementation of reference counting. To do this, it is worth adding a link field that is responsible for storing the number of vertices that refer to this one. It is logical to assume that if this field is not empty, then in no case can we just delete the current vertex, because this will affect the remaining versions of the tree. And yes, when deleting a vertex, we also reduce the link in its children and cause recursive deletion if it requires.

Now we can rightfully assert that we finally wrote the persistent deramid using an implicit key. Why do we need it? It can do exactly the same operations as a regular deramid using an implicit key, but unlike it, we can now copy pieces of an array, insert copies of pieces of an array back into an array, without fear of overlapping priorities or increasing communication time with full copying of deramids . An example of using persistent deramids.