Fractal Night
It was already the last hour of this Sunday, I was already thinking of going to bed, but the good sourcerer sent me a picture from my abandoned site, which can be seen below, and the text “beautiful!”. These pictures I painted five years ago, with the help of so-called. runaway algorithm, but for the applicability of this algorithm, you need to be able to split the plane into regions for a given set of transformations, then I didn’t figure out how to do this, and never returned to this algorithm. But now I immediately figured out what to do, and wrote to Dima: “First Random IFS, then kNN, and then Escape-Time Algorithm!”
I had only an old netbook on hand that my friends gave me for a while while my laptop was being repaired. Dima told me something else, I answered him something, but I already had the code written in my head, and I searched at least some compiler or interpreter on the netbook and found C ++ Builder 6! After that, I realized that in the morning I would meet alone with the Borland compiler. Five hours later, I sent Dima new pictures, but he, like a normal person, had long slept ...
')



So, a little bit of formulas. Imagine that we have a finite set of transformations of the plane T i : R 2 → R 2 , i = 1, ..., k . For an arbitrary set E, we define T ( E ) = T 1 ( E ) ∪… ∪ T k ( E ), that is, by each transformation we act on the set E , and combine the results. It can be proved that if the maps T i were contractive, then the sequence E , T ( E ), T ( T ( E )), ... converges to some set F for any non-empty compact E. This construction is known as a system of iterable functions .
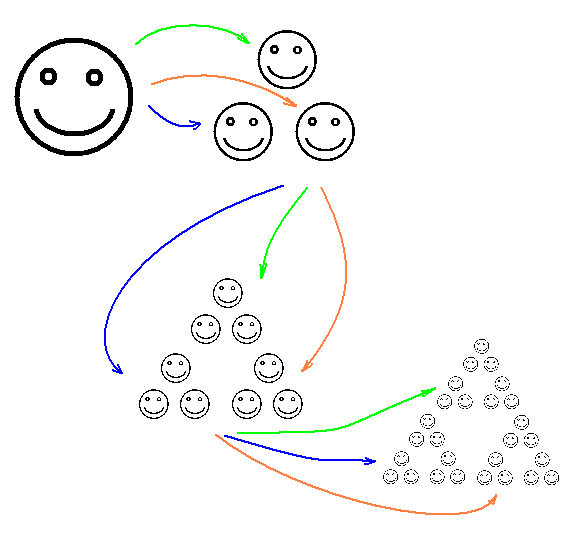
For example, if we take a smiley as a non-empty compact and consider three transformations, each of which is a composition of compression and shift to the i -th vertex of a regular triangle, then the first iterations will look like this, and in the limit we get the Sierpinski triangle:
Usually, instead of directly calculating the sequence E , T ( E ), T ( T ( E )), ..., so-called fracturers are used to construct fractals. "Game of chaos" , which is as follows. Choose an arbitrary point z 0 on the plane, then choose randomly the transformation T i 1 and calculate z 1 = T i 1 ( z 0 ), then again randomly choose T i 2 and calculate z 1 = T i 2 ( z 0 ), and m . e. It can be shown that everything will be fine, and the set of the obtained points will in some sense approximate the set F defined above. I will refer to this algorithm below as Random IFS.

Now it's time to go to the description of the escape time algorithm. Suppose we first have one transformation f . For each point z of the plane, we begin to calculate the sequence f ( z ), f ( f ( z )), f ( f ( f ( z ))), ... until either the number of iterations exceeds a certain given number N or the norm the number z will not exceed some number B. After this, the color of the point is selected in accordance with the number of iterations performed.
If for a while we imagine that our plane is complex, and the transformation f ( z ) is equal to z 2 + c , then as a result of the operation of this algorithm we obtain the Julia fractal set . You can read more about this in the habrastitia “Building a Julia set” by haphro user mephistopheies .

Suppose now that we have a system of iterable functions defined by a set of reversible compressing transformations of the plane T 1 , ..., T k . Let F be the attractor of this system.
Additionally suppose that the set F can be broken in such a way that T i ( F ) ∩ T j ( F ) = ∅, i ! = J (this assumption is far from being always fulfilled). We divide the entire plane R 2 into pieces A 1 , ...., A k so that T i ( F ) is a subset of A i for all i . We now define the function f ( z ) piecewise: on the set A i, we set f ( z ) = T k −1 ( z ) for all i .
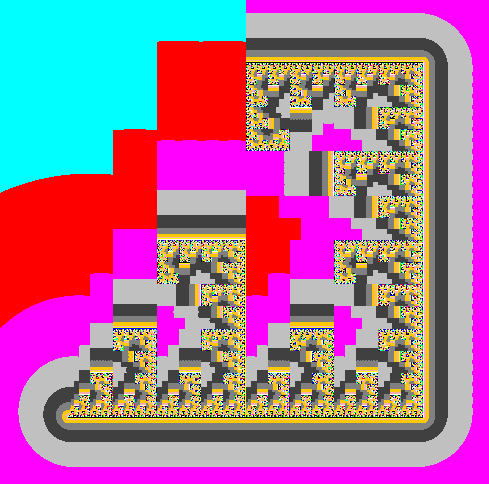
For example, for the Sierpinski triangle we consider such a partition (there are small problems with three points, but close our eyes to them).
And now the most important question is, what happens if we apply the escape time algorithm to the function f constructed in this way?
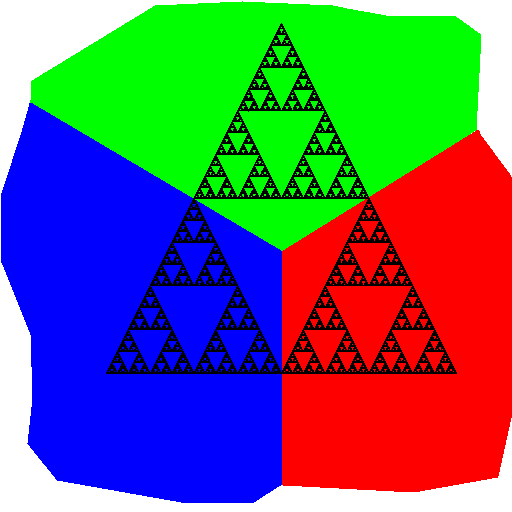
Let's get a look:

It turned out such a cute Sierpinski triangle!
It turns out this is not an accident. Just a couple of examples:




In these examples, the corresponding plane partitioning is not difficult to define analytically using Boolean combinations of circles and half-planes, using the gazing method. But often simple conditions can not be guessed. Therefore, instead of guessing, we will teach the computer to determine the partitioning on its own. This will help us the method of the nearest neighbor .
Namely, first with the help of Random IFS we generate several thousand points, and for each point we memorize the number of the transformation with which it was obtained. Then, during the EscapeTimeAlgorithm operation, for each pixel, we determine the area in which it falls using 1NN.
For example, for such an asterisk, 1NN gives the following partition into four pieces:


Putting it together, we get:

A few more pictures.




That's all. Finally, two comments.
First, the attentive reader may have wondered, since the fractals that are constructed using Random IFS can be constructed using the escape time algorithm, is it possible to build Julia's set using Random IFS? It turns out you can, you just need to reverse the mapping f ( z ) = z 2 + c , remembering how the root is extracted from the complex number. (However, when applying this method for constructing images of the Julia set, great difficulties arise.)

Secondly, the article described what is happening, if you want to know why this is happening, I recommend the book M. Barnsley "Fractals Everywere".
(Moments of source code can be found on github .)

I had only an old netbook on hand that my friends gave me for a while while my laptop was being repaired. Dima told me something else, I answered him something, but I already had the code written in my head, and I searched at least some compiler or interpreter on the netbook and found C ++ Builder 6! After that, I realized that in the morning I would meet alone with the Borland compiler. Five hours later, I sent Dima new pictures, but he, like a normal person, had long slept ...
')
So, a little bit of formulas. Imagine that we have a finite set of transformations of the plane T i : R 2 → R 2 , i = 1, ..., k . For an arbitrary set E, we define T ( E ) = T 1 ( E ) ∪… ∪ T k ( E ), that is, by each transformation we act on the set E , and combine the results. It can be proved that if the maps T i were contractive, then the sequence E , T ( E ), T ( T ( E )), ... converges to some set F for any non-empty compact E. This construction is known as a system of iterable functions .
For example, if we take a smiley as a non-empty compact and consider three transformations, each of which is a composition of compression and shift to the i -th vertex of a regular triangle, then the first iterations will look like this, and in the limit we get the Sierpinski triangle:
Usually, instead of directly calculating the sequence E , T ( E ), T ( T ( E )), ..., so-called fracturers are used to construct fractals. "Game of chaos" , which is as follows. Choose an arbitrary point z 0 on the plane, then choose randomly the transformation T i 1 and calculate z 1 = T i 1 ( z 0 ), then again randomly choose T i 2 and calculate z 1 = T i 2 ( z 0 ), and m . e. It can be shown that everything will be fine, and the set of the obtained points will in some sense approximate the set F defined above. I will refer to this algorithm below as Random IFS.
z = (0, 0) for (i = 0; i < maxIterNum; ++i) { cl = random([p1, ..., pk]) // pi -- , Ti. z = T[cl](z) if (i > skipIterNum) { // . draw(z) } } Now it's time to go to the description of the escape time algorithm. Suppose we first have one transformation f . For each point z of the plane, we begin to calculate the sequence f ( z ), f ( f ( z )), f ( f ( f ( z ))), ... until either the number of iterations exceeds a certain given number N or the norm the number z will not exceed some number B. After this, the color of the point is selected in accordance with the number of iterations performed.
for (y = y1; y < y2; y += dy) { for (x = x1; x < x2; x += dx) { z = (x, y); iter = 0; while (iter < N && ||z|| < B) { z = f(z) iter += 1; } drawPixel((x, y), color(iter)) } } If for a while we imagine that our plane is complex, and the transformation f ( z ) is equal to z 2 + c , then as a result of the operation of this algorithm we obtain the Julia fractal set . You can read more about this in the habrastitia “Building a Julia set” by haphro user mephistopheies .

Suppose now that we have a system of iterable functions defined by a set of reversible compressing transformations of the plane T 1 , ..., T k . Let F be the attractor of this system.
Additionally suppose that the set F can be broken in such a way that T i ( F ) ∩ T j ( F ) = ∅, i ! = J (this assumption is far from being always fulfilled). We divide the entire plane R 2 into pieces A 1 , ...., A k so that T i ( F ) is a subset of A i for all i . We now define the function f ( z ) piecewise: on the set A i, we set f ( z ) = T k −1 ( z ) for all i .
For example, for the Sierpinski triangle we consider such a partition (there are small problems with three points, but close our eyes to them).
And now the most important question is, what happens if we apply the escape time algorithm to the function f constructed in this way?
Let's get a look:

It turned out such a cute Sierpinski triangle!
It turns out this is not an accident. Just a couple of examples:




In these examples, the corresponding plane partitioning is not difficult to define analytically using Boolean combinations of circles and half-planes, using the gazing method. But often simple conditions can not be guessed. Therefore, instead of guessing, we will teach the computer to determine the partitioning on its own. This will help us the method of the nearest neighbor .
Namely, first with the help of Random IFS we generate several thousand points, and for each point we memorize the number of the transformation with which it was obtained. Then, during the EscapeTimeAlgorithm operation, for each pixel, we determine the area in which it falls using 1NN.
For example, for such an asterisk, 1NN gives the following partition into four pieces:

Putting it together, we get:
points = RandomIFS(Ts) classifier = kNN(points); for (y = y1; y < y2; y += dy) { for (x = x1; x < x2; x += dx) { z = (x, y) iter = 0 while (iter < maxIterNum && ||z|| < sqrdBound) { cl = classifier.getClass(z); z = T[cl].applyInvert(z); iter += 1; } draw((x, y), color(iter)) } } A few more pictures.
That's all. Finally, two comments.
First, the attentive reader may have wondered, since the fractals that are constructed using Random IFS can be constructed using the escape time algorithm, is it possible to build Julia's set using Random IFS? It turns out you can, you just need to reverse the mapping f ( z ) = z 2 + c , remembering how the root is extracted from the complex number. (However, when applying this method for constructing images of the Julia set, great difficulties arise.)
x = z0.re y = z0.im for (i = 0; i < N; ++i) { x -= c.re; y -= c.im; len = sqrt(x*x + y*y); ang = atan2(y, x); if (rand() % 2 == 0) { // - . x = sqrt(len) * cos(ang / 2); y = sqrt(len) * sin(ang / 2); } else { x = sqrt(len) * cos(ang / 2 + M_PI); y = sqrt(len) * sin(ang / 2 + M_PI); } draw(x, y) } Secondly, the article described what is happening, if you want to know why this is happening, I recommend the book M. Barnsley "Fractals Everywere".
(Moments of source code can be found on github .)
Source: https://habr.com/ru/post/240417/
All Articles