Adventures in the mathematical forest of fractal trees

Translation of the post Bernat Espigulé Pons, "Adventures into the Mathematical Forest of Fractal Trees" .
Download the translation in the form of a Mathematica document that contains all the code used in the article here .

Without a doubt, the golden section and in our time seems to be one of the most mysterious, magical and amazing numbers that are known to people: 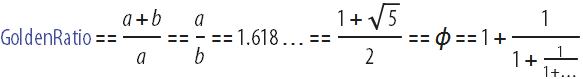. (in the Wolfram Language and Mathematica, the GoldenRatio symbol corresponds to it ). As you will see from this post, this number does have a lot of interesting properties that can be explored, some of which were considered in the works of scholars of ancient Greece, such as Pythagoras and Euclid , others in the works of the Italian mathematician Leonardo of Pisan , better known by the nickname Fibonacci , or Johann Kepler , an astronomer of the Renaissance. Although it may sound strange, in this post I will tell you about the new geometric objects related to the golden section, which illuminated my path when I tried to display the previously unknown area of ​​the Mathematical Forest.

The properties found below were not found by chance, I worked hard to get this new knowledge from the time when I was in high school. After in 2007 I saw the “golden” drawings (in terms of using the golden section fractal structure) of Hans Walser’s trees, I realized that there is still room for new research and discoveries in this area. After some searches, I found the tools I needed for this: the Mathematica system and the Theo Gray interactive model called “ Naked-blown Pythagoras blown tree ” interactive system, from the Wolfram Demonstrations Project website. Having gathered some knowledge and initial programming skills in the Wolfram Language, I got my first results and insights. Say, below you can see an example of one of the first self-touching “golden” fractal trees that I discovered by creating my own version of Theo Gray’s The Flexor, which I originally developed to study ternary trees (i.e. trees that have from each node there are three branches).
')
In [1]: =



Out [3] =



This is a self-similar tree, i.e. a tree, which is obtained, in fact, by the consistent application of a certain branching rule. I call “golden” those trees whose length of branches is a multiple of the golden section GoldenRatio = φ. For this particular tree, the scale factor for the central branch is , and for lateral branches . The angle between the central branch and each of the side branches is 72º. Since this tree has no intersecting branches or elements that are not interconnected, it can be called a “self-touching” tree. Let's take a closer look at some of its properties:

In [4]: ​​=



Out [7] =



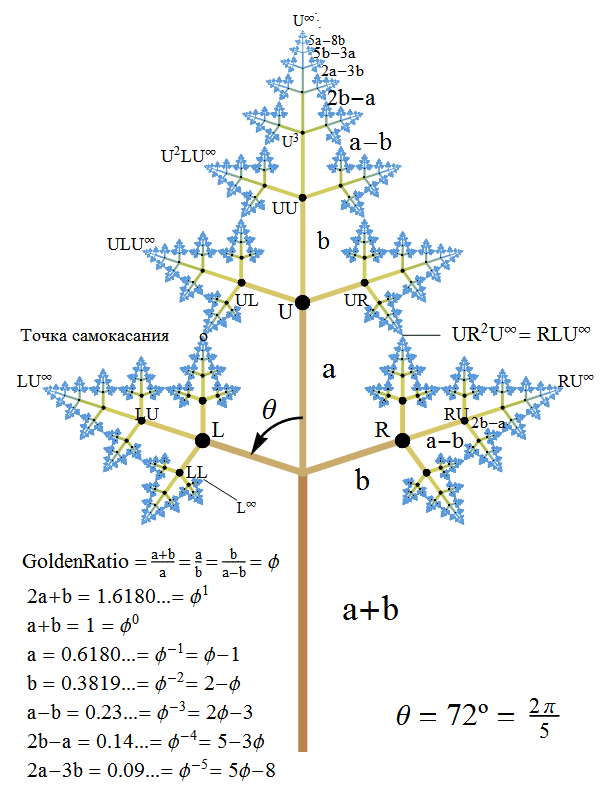
Following the designations proposed by Benoit Mandelbrot and Michael Frame for binary trees, I added the third letter U , with which we can describe all the branches of our triple tree. The letter L indicates the branches that go to the left, the letter R shows the branches that go to the right, and the letter U corresponds to the central branch. Thus, the string of these letters uniquely defines each branch of our fractal. In the event that this kind of “address” has infinite length, then we can indicate a specific “top” of our fractal tree, which can be considered, in fact, as an unattainable limit point, to which the chain of branches of the fractal tree is gradually approaching. For example, an endless “address” of the form sets the “tip” at the very top of our tree:

In [8]: =



Out [8] =



Thus, the height of our tree is:

In [9]: =



Out [9] =



And its width is equal to the distance between points. and :

In [10]: =



Out [10] =



It is also very interesting that the length of a sequence of tree branches can be expressed using Fibonacci numbers (in Mathematica , the Fibonacci [n] function serves to search for the nth Fibonacci number). You can find some expressions used in the code below in the lower left corner of the previous figure:

In [11]: =



Out [11] =



In [12]: =



Out [12] =



Finally, in order to prove that this tree is self-touching, we need to show that two different branches (their tops) touch each other at one point, which simultaneously corresponds to two points (tops) of the tree: . In this case, the same thing is observed for a mirror-symmetric point (see the diagram below). If this is so, then self-similarity of the tree will mean that there are no vertices in it that do not touch other vertices. This means that you can take any vertex, “cut off” a subset of the tree containing it, which repeats the entire tree in appearance, then change its scale accordingly, rotate it to the desired angle and we will get the point of tangency of one of the two main types considered. :



Vertex coordinates can be defined as follows:

In [13]: =



Out [13] =



The coordinates of the vertex will be equal to:

In [14]: =



Out [14] =



Thus, in view of the fact that these coordinates are equal, we can assert that our tree is indeed self-touching.

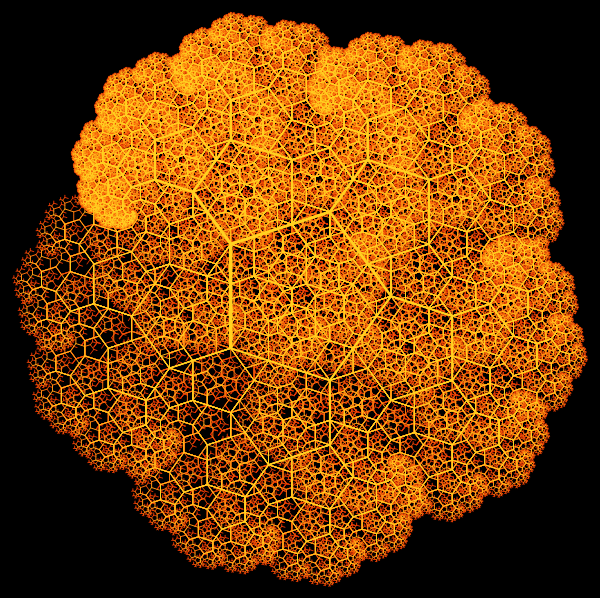
Another amazing thing associated with this “golden” tree is that it creates a beautiful 5th-order axial symmetry pattern, which can be obtained by rotating the main tree around its base:

In [15]: =



Out [17] =



Or you can create a similar pattern by rotating the tree around its main vertex:

In [18]: =



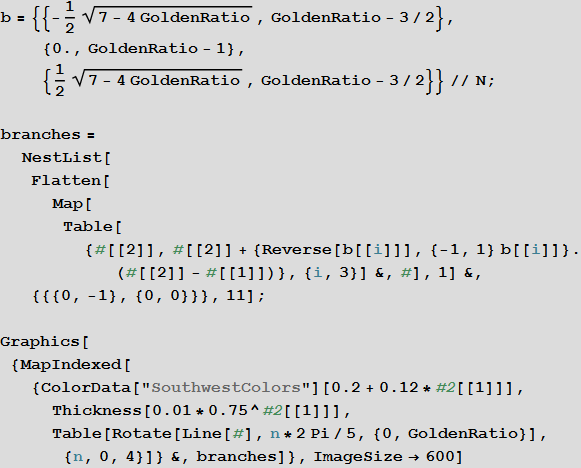
Out [20] =



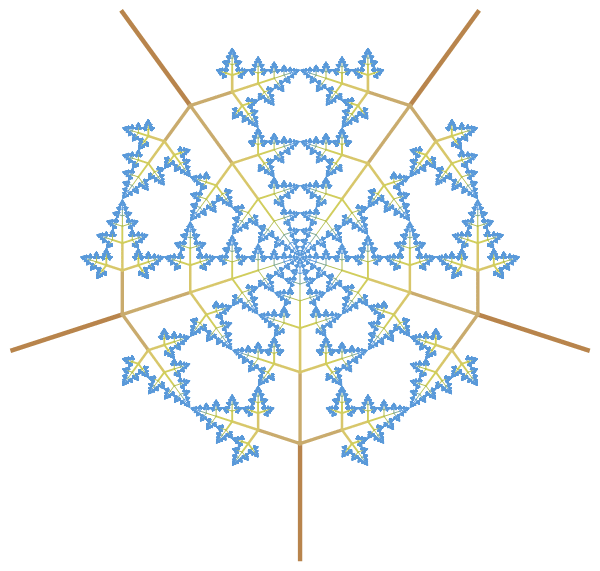
On the same day, I discovered a second triple “golden” tree. This tree, in which the central branch goes down, we denote it by the letter D , and the right R and left L branches form a 36º angle together with the central branch.

In [21]: =



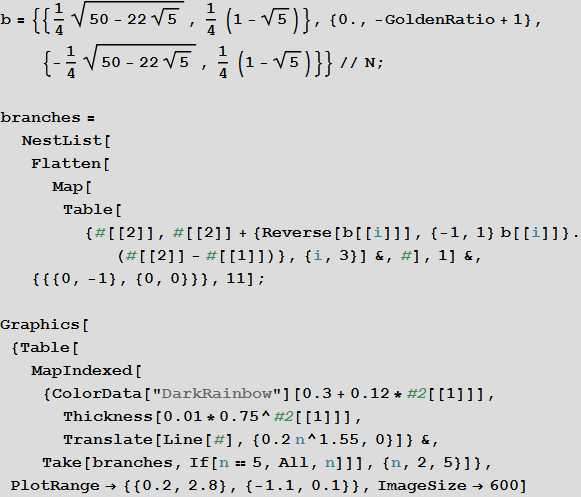
Out [23] =



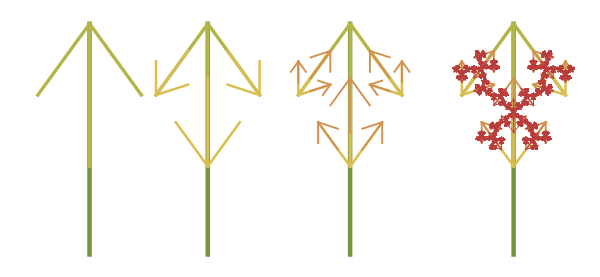
In this case, we can create a pattern with axial symmetry of the 10th order by rotating the created tree around its base:

In [24]: =



Out [26] =



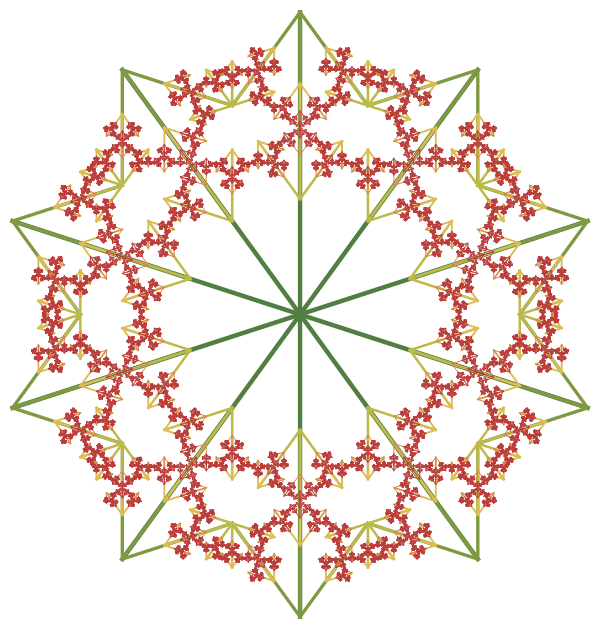
Now let me introduce to you the very first “golden” tree, which I discovered back in 2011:

In [27]: =



Out [29] =



This binary tree is asymmetrical. In it, the length of the branches that go to the left, at each step is multiplied by the coefficient while they form with an extension of the central branch an angle of 36º. The branches extending to the right are arranged in such a way as to form regular pentagons. The first four iterations are listed below:

In [30]: =



Out [32] =



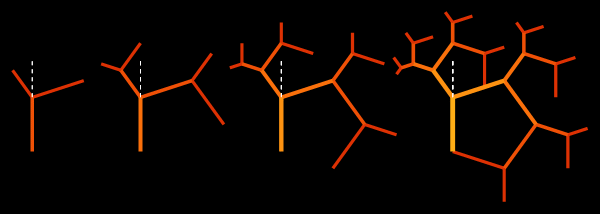
You can also consider an asymmetric tree, shown below, which has a mirror symmetry with respect to a straight line passing through the central branch:

In [33]: =



Out [37] =



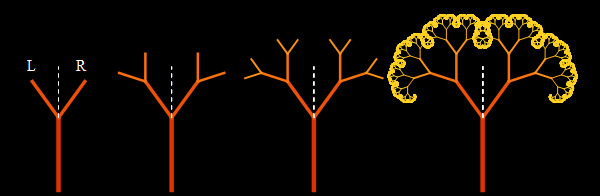
Based on this tree, you can create a fractal that has a 5th order axial symmetry:

In [38]: =



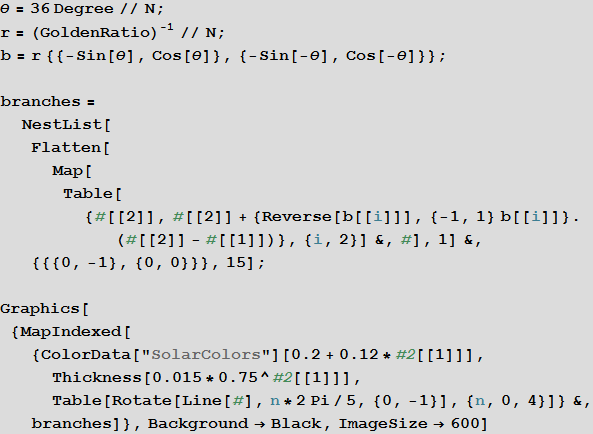
Out [42] =



The real magic happened after I “folded” this tree as shown in this gif-animation created with the help of Mathematica .



When the branches were fully folded, the tops of the tree formed a “golden” Koch snowflake . The golden section “built” the branches in such a way that they formed “ golden triangles ” and “ golden gnomons ”, which can be seen at any degree of magnification of the image.

In [43]: =



Out [43] =


( watch online CDF demo )

After the trees, whose ends of the maternal branches move clearly along a straight line, were considered, a whole family of self-touching binary trees appeared (about this you can read more in the post “ Automatic Drawing in Mathematica: Drakens Trees ”).

Then I began to consider trees that have more than two branches extending from the main branch. The collection of “ Fractal Mosaics” by Robert Fathauer inspired me to search for a way to display all possible trees that produce Koch's snowflakes, like the tree that was examined earlier, using a single diagram. This diagram was presented at last year’s Bridges conference (you can find the article by reference , the diagram itself is a figure with figure figure 4). These studies and observations allowed me to move forward and summarize the symmetric self-tapping binary fractal trees studied by Benoit Mandelbrot and Michael Frame (Michael Frame) (see [1] ), Tara Taylor (see [2] [3] ), Dushan Pagon (see [4] ) and Stephen Wolfram (see [5] ). After a long work on finding out how the “addresses” of the paths to the tree tops, in which it touches itself, are related to the angle θ, as well as the number of branches of the tree, using Mathematica, I managed to get all nine types of equations that determine the coefficient of self-touch for n -ary symmetric fractal trees. I will not go into details here - you can explore the self-shedding trees in the manipulator below. If you are interested in this question, you can read the post “ Nine equations to rule them all. The entire Sierpinski family of fractals ”(Nine equations to rule them all. The Sierpinski's whole family), which was written for the Wolfram Community. In this post, results are obtained, which were then published in the journal Symmetry (Volume 24, Numbers 1-4, pages 320–338, 2013).

In [44]: =



Out [44] =


( watch online CDF demo )

My research didn't end there. Last summer, during my first week at the Wolfram Science Summer School , I had the good fortune to open five three-dimensional self-touching infinite “golden” trees with branches pointing down (below you can see one of these trees generating a three-dimensional code snowflake can be obtained if we take the angle of inclination of the side branches relative to the extension of the central branch to be 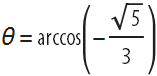). This moment became for me the most outstanding.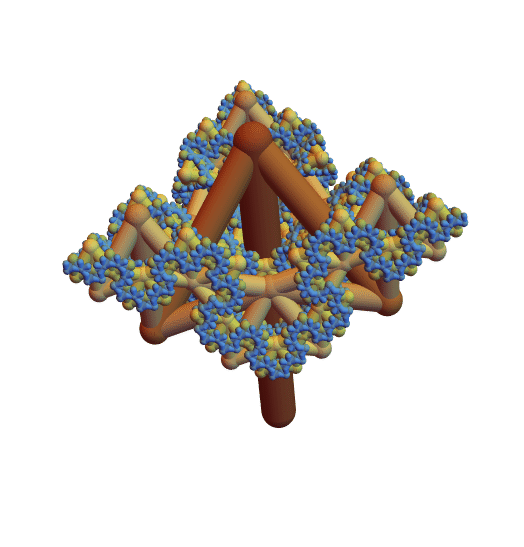



When I arrived at the Wolfram Science Summer School, I already had some vague vision of what I would do about the project. I wanted to generalize the equations I found for two-dimensional fractal trees for a three-dimensional case. I tried to do this before, but I had certain difficulties in applying all sorts of rotations, and I could only create a small set of highly symmetrical trees, like a tetrahedral tree , which I printed on a 3D printer just before joining summer school. The demonstration of “ Tree Branching in 4D ” by Todd Rowland, the academic director of the summer school, helped me to understand the main ideas of my project, and my leader, Vitaliy Kaurov , was very inspired by my goal .



After my first conversation with Stephen Wolfram (Stephen Wolfram), everyone agreed that I should stay in the same Mathematical Forest from which I came and should try to move on to the higher dimension of the trees in question. During my first week, I searched for literature on three-dimensional fractal trees, and I found an article “Symmetric Fractal Trees in Three Dimensions” written by Frongillo et al., As well as Paul Nylander’s example generating three-dimensional ternary fractal trees. After that, I quickly tried to reproduce and expand the results presented in the article, based on my intuition and knowledge gained from studying two-dimensional trees under the guidance of Susanne Krömker at Heidelberg University. The final results were astounding and I am still amazed at how quickly all these equations were obtained in just three weeks. Of course, the atmosphere that stood in the summer school was the best assistant for the implementation of such a project.

“Simple rules that are applied infinitely many times are an inexhaustible source of miracles.” - Benoit B.Mandelbrot

In [45]: =



Out [45] =


( watch online CDF demo )

(A manipulator created using the Manipulate function, which you see above, will allow you to explore the “forest” of symmetric binary fractal trees. The blue “map” in the background is the Mandelbrot set for symmetric binary trees. In this case, the Julia set associated with this "map" is the set of vertices of the respective trees. this "map", opened by Michael Barnsley (Michael Barnsley), has some common features with the dot cards , open Stephen Wolfram (Stephen Wolfram). The imaginary axis is directed at the e Figure ohm up to trees "growing" upwards. In this case in the center of the white area corresponds to the provisions of the parent branch at which derived from them are disconnected trees).