Transition from an approximate solution to an exact one: the problem of splitting a square into 50 similar acute-angled triangles

Translation of Ed Pegg Jr's post (Ed Pegg Jr) " From Close to Perfect — A Triangle Problem "
I express my gratitude for the help in translating Andrei Dudin .
Download the translation in the form of a Mathematica document that contains all the code used in the article here .

In the Wolfram Language (available, say, in Mathematica), the RootApproximant function allows us to find a closed form as an algebraic number for some approximate number, and this function allowed us to transform an approximate solution of the problem of splitting a square into 50 similar acute-angled triangles with angles (45 ° , 60 °, 75 °) to the exact.
')
It is clear that a square can be divided into triangles (triangulated), for example, simply by connecting its opposite vertices. It is also known that the square can be divided into seven similar triangles of different area or ten acute-angled isosceles triangles (see the figure below). There are also classical problems associated with splitting a square into eight acute triangles (see the figure below), or into twenty triangles with sides that refer to each other as . The third drawing (counting from above) shows a splitting of a square into similar triangles with angles (45 °, 60 °, 75 °), but you can easily notice that this solution is not correct, since one of the triangles superimposes a little on the other.

In [1]: =



Out [9] =







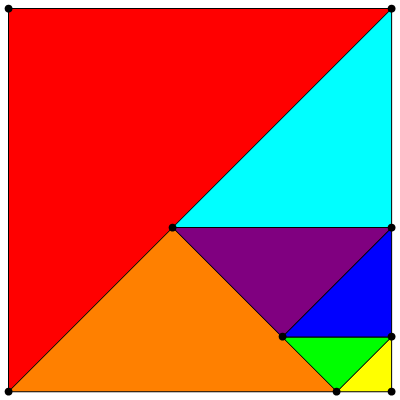
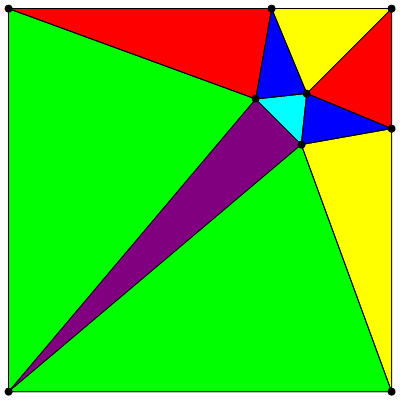
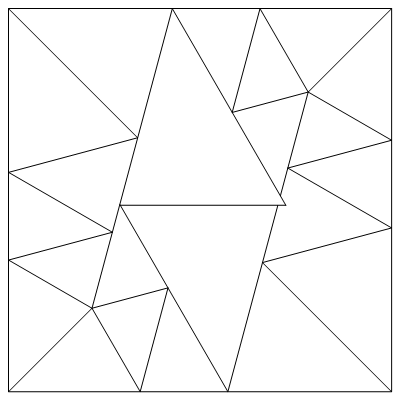
You can easily find a partition of a square into similar right triangles. But is it possible to find a partition of a square into similar non-rectangular triangles? In his article “ Tilings of Polygons with Similar Triangles ” (“Splitting polygons into similar triangles”) ( Combinatorica , 10 (3), 1990 pp. 281–306), Laskovich (Laczkovich) proved that this is possible only for three types of triangles with angles (22 ° 30 ', 45 °, 112 ° 30'), (15 °, 45 °, 120 °) and (45 °, 60 °, 75 °). I read this article and tried to find explicitly splitting the square into similar triangles with angles (45 °, 60 °, 75 °), but the construction of such a partition turned out to be difficult, and I had the feeling that to solve this problem it would be necessary to use thousands of such triangles. In all my decisions there were flaws similar to what was shown above, so I decided to organize a small competition : the reward for the found splitting is $ 200 minus a dollar for each triangle in the found solution.

Lew Baxter began (Lew Baxter) with a careful study of Laskovich’s approach, and was able to find a solution using 7 trillion triangles. But he found a way to improve this solution and wrote a program to find more optimal solutions. Within a few weeks, he received a solution containing 198 triangles, which would be enough to get a prize of $ 2 from me. But he continued his search and finally came to a solution containing only 64 triangles. Unfortunately, the coordinates of all the vertices of the triangles were found approximately, albeit with great accuracy. At that moment it seemed that the solution that I give below is optimal, and it would not be possible to find a better solution, also in a closed form. In the figure below you can see the found splitting for half of the square, it is clear that it is enough to reflect this decision relative to the diagonal of the square to get the solution of the original problem.

In [10]: =



In [11]: =



In [12]: =



Out [12] =



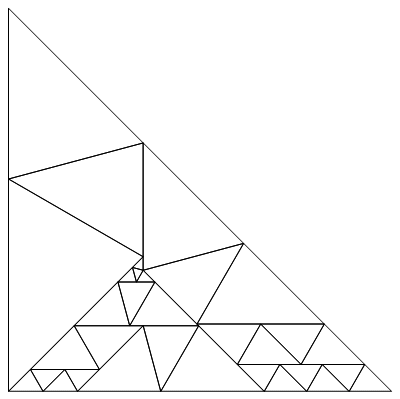
To construct an exact solution for this approximate solution, you can use the RootApproximant function, which searches for the root of a certain polynomial, which will approximate this approximate number with a given accuracy. In geometric problems like the one we are considering, very often the exact solution is just the set of roots of some polynomials. For the task in question, I tried the following: using the RootApproximant function, possible closed forms were found for each of the coordinates, which were then multiplied by 4686 in order to get rid of fractions. All values, as is easy to see, have the form that seems pretty encouraging.

In [13]: =



Out [13] =



Below you can look at the resulting solution containing 64 triangles.

In [14]: =



Out [14] =



Then, I received a new message from Lew - if you work a little with triangles 6, 7, 21, and 22, you can end up replacing seven triangles with just one.



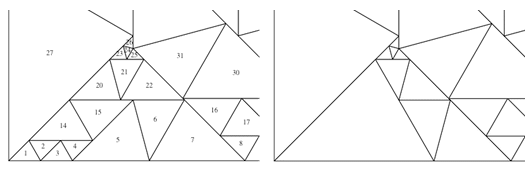
I calculated a new set of exact vertex coordinates, although it was not very simple.

In [15]: =



In [16]: =



The result was a solution containing 50 triangles. Is this an exact solution? Using the code below, we calculate the angles of all triangles.

In [17]: =



In [18]: =



Out [18] =



It is easy to see that each of the triangles has angles equal to exactly (45 °, 60 °, 75 °), so Baxter’s solution is actually exact. Now we can look at the solution containing 50 triangles.

In [19]: =



Out [19] =



So, I owe Lew Bakster $ 150. If you have ever dealt with the problems of numerical optimization and the search for an exact solution is difficult and incomprehensible, you should probably try using functions like RootApproximant in the Wolfram Language.