Summation of divergent series by the methods of Abel, Borel, Cesaro and Dirichlet

Translation of Davendra Kapadia's post " The ABCD of Divergent Series ."
I express my gratitude for the help in translating Andrei Dudin .

What is the sum of all natural numbers? Intuition suggests that the answer is infinity. In mathematical analysis, the sum of natural numbers is a simple example of a divergent series. Nevertheless, mathematicians and physicists found it useful to give fractional, negative, and even zero values ​​to the sums of such series. The purpose of my article is the desire to remove the veil of secrecy surrounding the results of the summation of divergent series. In particular, I will use the Sum function (the search function for partial sums, series, etc. in Mathematica ), as well as other functions in the Wolfram Language to explain in what sense the following statements should be considered:


')
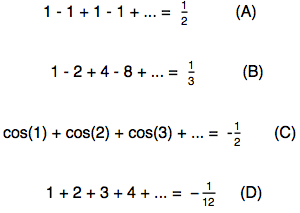
The importance of the designations of formulas with the letters A, B, C, and D will soon become clear to you.

To begin with, recall the notion of a convergent series using the following infinitely decreasing geometric progression.



The common member of the series, starting with n = 0 , is determined by the formula:

In [1]: =



Now we define the sum of the series members from i = 0 to some final value i = n .

In [2]: =



This finite sum is called the partial sum of the series .

The graph of the values ​​of such partial sums shows that their values ​​approach the number 2 with increasing n :

In [3]: =



Out [3] =



Using the Limit function (searching for the limit of a sequence or a function at a point), we find the limit of the value of the partial sums of this series as n tends to infinity, which will confirm our observations.

In [4]: ​​=



Out [4] =



The Sum function gives the same result when we perform the summation of the series in the range from 0 to infinity.

In [5]: =



Out [5] =



We say that a given series (the sum of a given infinitely decreasing geometric progression) converges and that its sum is 2.

In general, an infinite series converges if the sequence of its partial sums tends to some value with an unlimited increase in the number of the partial sum. In this case, the limit value of partial sums is called the sum of a series.

An infinite series that does not converge is called divergent . By definition, the sum of the divergent series cannot be found using the partial sum method discussed above. However, mathematicians have developed various ways of assigning finite numerical values ​​to the sums of these series. This sum is called the regularized sum of the divergent series. The process of calculating regularized sums is called regularization .



Now we look at example A from the introduction.



“A” stands for Abel, a famous Norwegian mathematician, who proposed one of the regularization techniques for divergent series. During his short life, he died at just 26 years old, Abel achieved impressive results in solving some of the most difficult mathematical problems. In particular, he showed that a solution to a fifth-degree algebraic equation cannot be found in radicals, thereby putting an end to the problem that remained unsolved for 250 years before it.

In order to apply the Abel method, we note that the common member of this series has the form:

In [6]: =



This can be easily verified by finding the first few values ​​of a [ n ].

In [7]: =



Out [7] =



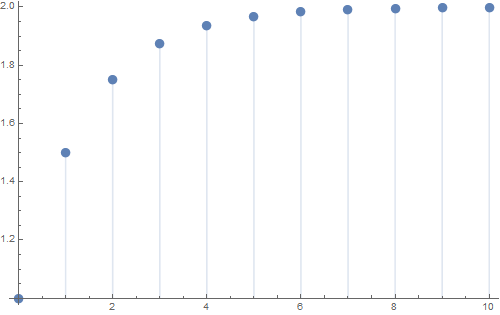
As can be seen in the graph below, the partial sums of a series take values ​​of 1 or 0, depending on whether it is even n or odd.

In [8]: =



Out [8] =



Naturally, the Sum function issues a message stating that the row diverges.

In [9]: =





Out [9] =



Abel regularization can be applied to this series in two steps. First we build the corresponding power series.

In [10]: =



Out [10] =



Then we take the limit of this sum when x tends to 1, and note that the corresponding series converges for values ​​of x smaller, but not equal to 1.

In [11]: =



Out [11] =



These two steps can be combined to form, in essence, the determination of the sum of the divergent series according to Abel .

In [12]: =



Out [12] =



We can get the same answer using the Regularization option for the Sum function as follows.

In [13]: =



Out [13] =



The value 1/2 is reasonable, since it is the average of two values, 1 and 0, taken as a partial sum of this series. In addition, the transition used in this method is intuitive, since the power series at x = 1 coincides with our divergent series. However, Abel was deeply concerned about the lack of rigor that was inherent in the mathematical analysis of the time, and expressed his concern about this:

“Divergent ranks are the invention of the devil, and it is embarrassing to refer to them in any evidence. With their help, any conclusion can be made which is pleasing to him, and that is why these series produce so many mistakes and so many paradoxes. ”(N. H. Abel in a letter to his former teacher Berndt Holmboy, January 1826)



Let us now turn to example B, which states that:



“B” refers to Borel, a French mathematician who worked in such areas as measure theory and probability theory. In particular, Borel is associated with the so-called “endless monkey theorem,” which states that if an abstract monkey randomly strikes a typewriter keyboard for an infinite amount of time, then the probability that it will type some specific text, for example, complete Collected works of William Shakespeare, different from zero.

In order to apply the Borel method, we note that the common member of this series has the form:

In [14]: =



Borel's regularization can be applied to rapidly diverging rows in two steps. In the first step, we calculate the exponential generating function for the sequence of members of this series. The factorial in the denominator ensures the convergence of the given series for all values ​​of the parameter t .

In [15]: =



Out [15] =



Then we produce the Laplace transform of our exponential generating function and look for its value at the point s = 1 .

In [16]: =



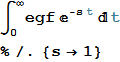
Out [16] =



Out [17] =



These steps can be combined; as a result, we will obtain, in essence, the determination of the sum of the divergent series according to Borel .

In [18]: =



Out [18] =



We can also use Wolfram Language’s specialized functions to search for the exponential generating function and the Laplace transform:

In [19]: =



Out [19] =



In this case, the answer can be obtained directly using Sum as follows.

In [20]: =



Out [20] =



Determining the Borel sum is reasonable, because it gives the same result as the ordinary partial sum method, if applied to the convergent series. In this case, you can swap the summation and integration, and then determine the Gamma function , and we will get that the corresponding integral will be equal to 1 and the simple sum of the series will remain:

In [21]: =



Out [21] =



However, in the case of divergent rows, the signs of the sum and integral cannot be interchanged, which leads to interesting results, which are given by this regularization method.

Borel summation is a universal method of summation of divergent series, which is used, say, in quantum field theory. There is a huge collection of literature on the application of Borel summation.



Example C states that:



“C” stands for Cesaro (in English, his name is spelled Cesaro), an Italian mathematician who made a significant contribution to differential geometry, number theory, and mathematical physics. Cesaro was a very productive mathematician and wrote about 80 works in the period from 1884 to 1886, before he received his PhD in 1887!

To begin with, we note that the common member of the series, starting with n = 0, has the form:

In [22]: =



The graph shows a strong oscillation of the partial sums of this series.

In [23]: =



Out [23] =



The Cesàro method uses a sequence of arithmetic means of partial sums of a series in order to suppress oscillations, as the following graph shows.

In [24]: =



Out [24] =



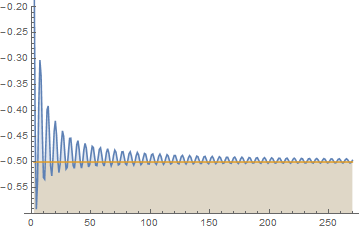
Formally speaking, Cesaro summation is defined as the limit of the sequence of arithmetic mean values ​​of partial sums of a series. By calculating this limit for the series from Example C, we get the result we expect to be -1/2 (see the graph above).

In [25]: =



Out [25] =



The Cesàro amount can be obtained directly if we use this type of regularization in the Sum function, specifying the appropriate value of the Regularization option.

In [26]: =



Out [26] =



The Cesàro summation method plays an important role in the theory of Fourier series , in which series based on trigonometric functions are used to represent periodic functions. The Fourier series for a continuous function may not converge, but the corresponding Cesàro amount (or the Cesáro average, as it is usually called) will always converge to the function. This beautiful result is called the Fejer theorem.



Our last example states that the sum of the natural series is -1/12.



“D” means Dirichlet, a German mathematician who made a huge contribution to number theory and a number of other areas of mathematics. The breadth of Dirichlet contributions can be judged by simply entering the following code in Mathematica 10.

In [27]: =



Out [27] // TableForm =



Dirichlet regularization got its name from the concept of “Dirichlet series”, which is defined as follows:



A special case of this series is the Riemann zeta function , which can be defined as:

In [28]: =



In [29]: =



Out [29] =



The SumConvergence function tells us that this series converges if the real part of the parameter s is greater than 1.

In [30]: =



Out [30] =



However, the Riemann zeta function itself can be determined for other values ​​of the parameter s using the process of analytic continuation, known from the theory of functions of a complex variable. For example, when s = -1, we get:

In [31]: =



Out [31] =



But with s = -1, the series defining the Riemann zeta function is the natural series. From here we get that:

In [32]: =



Out [32] =



Another way to realize this result is to enter the infinitesimal parameter ε into the expression of a member of our divergent series, and then find the decomposition of the obtained function into the Maclaurin series using the Series function, as shown below.

In [33]: =



Out [33] =



First term in the expansion above, tends to infinity as the parameter ε approaches zero, while the third term and all the following members tend to zero. If we drop all the terms depending on ε, then the remaining number -1/12 will be the Dirichlet sum of the natural series. Thus, the Dirichlet sum is obtained by discarding the infinitely small and infinitely large terms of the expansion of the series constructed by the method described by us. This is in contradiction with the fact that it is customary to discard only infinitely small values ​​in ordinary mathematical analysis, therefore the result of summing up divergent Dirichlet series is not so intuitive.

Similarly, you can get an incredibly strange value of 0 for a divergent sum of squares of positive integers.

In [34]: =



Out [34] =



In this case, in the corresponding decomposition there are no terms that are not dependent on the parameter ε, as a result we get 0.

In [35]: =



Out [35] =





Dirichlet's regularization is closely related to the zeta regularization process, which is used in modern theoretical physics. In his famous work, the eminent British physicist Stephen Hawking applied this method to the problem of computing Feynman integrals in a curved space-time. Hawking's article describes the zeta regularization process very systemically and it became very popular after publication.

Our knowledge of divergent ranks is based on the deepest theories developed by some of the best thinkers of the past few centuries. Nonetheless, I agree with many readers who, like me, feel some misunderstanding when they see them in modern physical theories. Great Abel was probably right when he called these series “the invention of the devil”. It is possible that some future Einstein, who has a mind free from all sorts of principles and authorities, will reject the prevailing scientific beliefs and reformulate fundamental physics so that there will be no room for divergent series. But even if such a theory becomes a reality, the divergent series will still give us a rich source of mathematical ideas, illuminating the road to a deeper understanding of our Universe.