Equation or all the same observation?

Father: Make yourself comfortable, Bug, we will conduct mental experiments with free-falling bodies with you today.
Bug: And how is that? Will the bodies fall in my mind? Right and I see: naked bodies flying against the starry sky ...
Father: The bodies are, of course, imaginary, but not so large as to be naked. In general, we are talking about the free fall of bodies in a uniform gravitational field.



Bug: What is this such a dream projector?
Father: This is my experimental project. So far this is a bunch of scary Python code using IPython for the binding. Well, let's get back to our conversation. So, a body falling freely at an initial speed moving with acceleration ...
Bug: Again you mumble under your breath all sorts of incomprehensible curses. Many times I have seen how pieces of butterflies fly, which I devour with pleasure every day. And your projector can show what happens if you scatter a bunch of bits of space in different directions? I'm here thinking about a new way of babo gutting ... I'm sorry, absorption of lunch.
Father: You always think about food, Bug. In general, yes, we can simulate such a situation. Let's assume that all the pieces fly out of one at the same speed, and follow their flight for the first few seconds.

')
Bug: Wow, salute!
Father: Really, it seems? Anything else you notice?
Bug: Hmm, it looks like the pieces form a circle ... always ... a curious picture. And why is this happening?
Father: Before I explain, notice that you have recognized that it is a circle without any calculations and formulas. Even in the projector, if you look, there is no indication anywhere that the pieces should always form a circle. I just told the projector to emulate a lot of flying pieces and everything, and already your brain itself noticed the pattern without any abstruse explanations and formulas. The main thing is to ask an interesting question and have such a projector on hand!

And now I will try to explain why this picture is obtained. Imagine that you are one of the small pieces flying along with the rest. However, you were not thrown along with everyone, you managed to slip away and you fell out of the nest without initial speed. A little coming to yourself, you start to look around and watch the rest of the pieces. How do you think what their behavior will be like?
Bug: Well, they probably will be moving away from me, as they were thrown out of the nest.
Father: That's right, in the frame of reference associated with you falling freely, the force of attraction will not act, which means that the pieces will move away from you, moving with the same speed evenly and straightforwardly.
Bug: Wow, how did you start to be clever again. But I caught the point: the pieces will run away from me like a bicycle, and in general they will form a circle like a bicycle wheel. Can this be "seen" in your projector?
Father: You can, and this will be an exercise for you at home. And also try to prove formally that the pieces will always form a circle using formulas for free fall.

Bug: Okay, okay. And what else can be interesting to see in your projector?
Father: I will tell you about one method of finding curious properties of ordinary phenomena. Do you remember that freely falling bodies move, in general, along a parabola?
Bug: So what you have there is drawn like a tail in the stars in the projector! Yes, something about my parabolas remained in my memory.
Zpyatoshka: Very good! Let's see in the encyclopedia what interesting properties a parabola has. To begin with, let's see what the picture will turn out if we mark the vertices of the trajectories of the pieces, the flight of which we admired above.
Bug: And how do you explain to the projector where to put the mark?
Father: Well, we can do it in two ways. If we were investigating an unknown phenomenon, then we could simply explain to the projector how to find the local maximum of the trajectory. But we know how the body moves in the field of the earth, so we will try to find a formula for the coordinates of the vertex, and at the same time we will see how the sympy package can help us in this, which can solve all sorts of tasks in a symbolic form.

 v_x = v_0 * cos(alpha) v_y = v_0 * sin(alpha) - g * t (Eq(Symbol('v_x'), v_x), Eq(Symbol('v_y'), v_y)) 

Father: Now let's calculate the coordinates of the piece, considering that we started it from the point (0,0). To do this, it is necessary to integrate the speed over time.

 x_t = integrate(v_x, t) y_t = integrate(v_y, t) (Eq(x, x_t),Eq(y, y_t))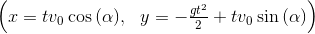 

Bug: wait, wait! I'm confused a bit. Why do you write Symbol ('v_x')? Why can't I just specify the v_x variable to see the resulting equation? And you somehow strangely derive the equations themselves ...
Father: you are very observant, Bug, well done! This is because the v_x variable and the v_x symbol are different entities. You can read more here .
Father: Vertical speed at the top of the trajectory where we find the moment of time 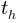when this happens.

 solution=solve(v_y, t) t_h = solution[0]; t_h 

Father: Finally, the coordinates of the vertex of the parabola:

 x_h = x_t.subs(t, t_h);x_h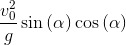 

 y_h = y_t.subs(t, t_h);y_h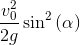 

Father: We teach our projector this knowledge and see what happens.


Bug: Stunned! This is ... this is ... Ellipse! Well, very similar!
Father: Well done, Bug. Notice, you first saw the picture, and the brain itself already suggested to you a pattern that could not be noticed no matter how much we stared at the formulas.
Bug: Fuck, I seem to be starting to understand why you are messing with your projector. And we will prove that this is really an ellipse, and not a fiction of our imagination?
Father: Of course, let's try to do it. True, we have to sweat a bit explaining what sympy we want to achieve. In essence, it is necessary to get rid of the angle in the expressions for the vertices of the parabolas, and to obtain a formula connecting 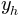and . If you try to solve the forehead:

 solve([x-x_h, y-y_h], [y, alpha]) 

Fatherie: it will turn out abracadabra (check yourself at home). And all because sympy is still small, does not know how to elegantly manipulate trigonometric expressions. But we will help him. To start:

 x_h = trigsimp(x_h); x_h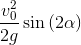 

Fatherie: further note that in the expression for 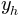you can make a replacement 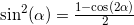. Make the substitution and get:

 y_h = y_h.subs(sin(alpha)**2, (1-cos(2*alpha))/2);y_h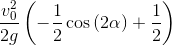 

Bug: Something tells me that you want to use equality
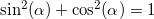
Father: Immediately it is clear that long nights of training were not in vain for you. Express 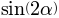and through and .

 s = solve([x-x_h, y-y_h], [sin(2*alpha), cos(2*alpha)]);s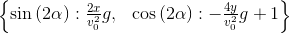 

Fatherie: and substitute in the equality noted by you:

 Eq(s[sin(2*alpha)]**2 + s[cos(2*alpha)]**2, 1)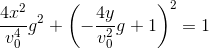 

Father: We get nothing like the equation of an ellipse!
Bug: Hmmm ...
Father: Here's another homework for you: find out how the shape of the ellipse changes depending on the initial speed, as well as the coordinates of its center, you can also explore tricks. Hint: find the eccentricity of the ellipse. He, as you remember, defines the shape of an ellipse.

Bug: Okay, okay, you're not the only one so smart, I'll figure it out somehow. You'd better show me something else, but you’ve found some kind of ellipse and you are happy like a child ...
Father: Well, I'll show you! We read the above mentioned encyclopedia further and find there a description of the focus of the parabola. What we immediately have a question? In your acid mine, it is immediately clear that we want to mark the tricks of all our parabolas and see what happens.
Bug: What, again, an ellipse?
Father: How do I know? Let's watch. In view of symmetry, the abscissa of the focus coincides with the abscissa of the top of the parabola. But the ordinate will need to find the formula 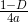according to the encyclopedia. To do this, we first find the equation of the parabola through and get rid of it from .

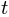 ss = solve([x-x_t,y-y_t], [y,t], dict=True);ss 

Fatherie: Therefore, the coefficients of the quadratic triple:

 a,b,c = ss[0][y].as_poly(x).all_coeffs(); a,b,c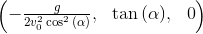 

Father: Then try it yourself.
Bug: Well, then the discriminant will turn out like this:

 D = b**2 - 4*a*c; D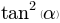 

Bug: and focus ordinate:

 y_f=(1-D)/(4*a);y_f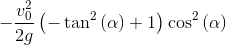 

Bug: What happens if you substitute it in your projector, wop?
Father: But what!


Bug: I have no words! Something looks like a sacred sign ... I remembered! Eye of Ra!
Father: Well, you have imagination, Bug. Try to prove that the tricks fall on the circle?
Bug: So, first we try to simplify:

 y_f = trigsimp(y_f); y_f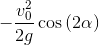 

Bug: Uh, everything here just turns out! You don’t even need to sweat, just fold the abscissa and ordinate squares:

 Eq(x**2 + y**2, simplify(x_h**2 + y_f**2))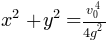 

Father: Well, since you are such a good fellow with us, here is another one of your tasks for the house. Learn how the directors of our parabolas behave.
Bug: And what if I have difficulties?
Father: Try to figure it out yourself, remembering that our tools are still far from perfect and they need to be occasionally helped and prompted. If all the questions remain, we will meet again and talk.

Finally, the last problem: look carefully at the very first picture at the beginning of our conversation - see, is there another figure looming on the background? Try to figure out what kind of figure it is and how it behaves.

Here's a couple more resources for inspiration.

• JL Fernandez-Chapou et al., An elliptic property of parabolic trajectories
• "Dream Projector": source code
• Bret Victor, Up and Down the Ladder of Abstraction
• Bret Victor, Simulation as a Practical Tool