Calculated knowledge and the future of pure mathematics

Translation of the post by Stephen Wolfram (Stephen Wolfram) " Computational Knowledge and the Future of Pure Mathematics "
I express my deep gratitude to those who helped me to make this translation: Vladislav Glagolev ( Himura ), Ilya Marchevsky , Sergey Shevchuk ( opckSheff ) and Anna Kovalenko .

Introduction

For more than a century, the International Congress of Mathematicians (ICM) has been held at some point in the world every 4 years. In 1900, it was there that David Hilbert presented his famous collection of problems in mathematics, which to this day sets the direction for research to mathematicians from all over the world.
')
This year ICM is taking place in Seoul, and today I am going there. I once visited ICM - in Kyoto in 1990. Then the Mathematica system was only 2 years old, and mathematicians were just beginning to get used to it. Many have already used it everywhere, but on ICM there were those who said “I am engaged in pure mathematics. What, I wonder, can Mathematica help me? ”



24 years later, most experts in the field of pure mathematics around the world, one way or another, use the Mathematica system. But, nevertheless, a large number of pure mathematicians continues to do everything just as it has been done for centuries - by hand and on paper.

Since attending the ICM congress in 1990, I have not ceased to reflect on how technology can be introduced into this traditional process. And now I can not wait to tell you that, apparently, I began to understand how this can be done. Although it should be noted: many details are still unknown to me. But in order to accomplish this, the support and cooperation of most pure mathematicians all over the world will be needed. If everything works out - the result promises to be impressive - it will definitely force the pure mathematicians to change their working methods as much as the Mathematica system (and for the younger generation, Wolfram | Alpha) changed the whole computational mathematics. Potentially, this result is able to bring pure mathematics into a new golden age.

Workflow pure mathematics

In general, this issue is very complicated. But for me, one of the most important starting points is the difference in the methods used in computational mathematics and pure mathematics. In computational mathematics, a specific computational problem is usually posed, which is then solved in order to get a result - just like a typical work session in Mathematica . In pure mathematics, on the contrary, some mathematical objects, results or structures are taken, some hypotheses are formed about them and then proofs of the hypotheses put forward are given.

How to effectively bring technology into such a workflow? There is one simple way to remember Wolfram | Alpha. If you enter 2 + 2 , then Wolfram | Alpha, in the same way as Mathematica , will give you 4. 4. But if you enter, say, “ new york ”, “ 2.3363636 ”, or “ cos (x) log (x) ” , then a simple "answer" that can not be counted. Instead, Wolfram | Alpha will generate a report containing a set of “interesting facts” about the data you entered.



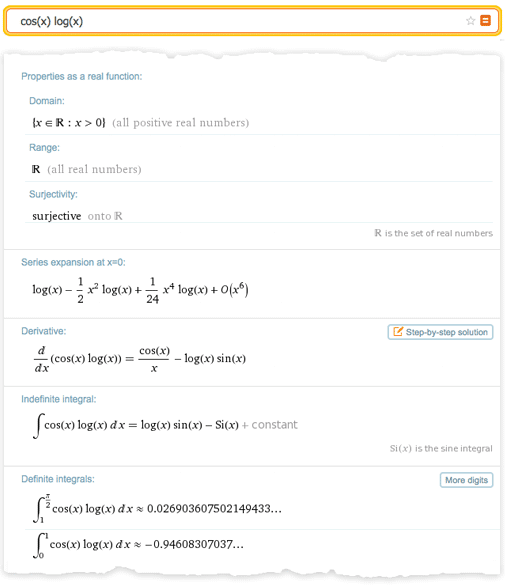
Answers of this kind fit perfectly into the workflow of pure mathematics. You enter some mathematical object, result or structure, and the system tries to tell something about them, just as your very wise mathematician could do. If necessary, you can tell the system what you want to know specifically, or even just indicate some statement that may be true. But working at Wolfram | Alpha always looks like searching for an answer to a question like “What can you tell me about it?”, Whereas in Mathematica the question in the spirit of “What is the answer to what I asked?”.

Wolfram | Alpha can already do a lot with all sorts of mathematical objects. For example, enter a number , a mathematical expression , a graph , a distribution of probabilities , whatever — and Wolfram | Alpha will use complex algorithms, trying to tell some interesting things about the entered data, structured into detailed reports.



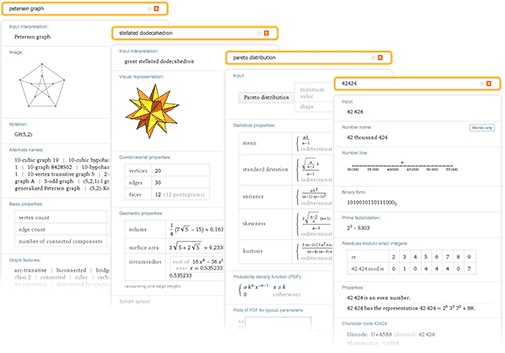
But in order to actually be useful when working with pure mathematics, the Wolfram | Alpha system needs something else. In addition to working with specific mathematical objects, the ability to work with abstract mathematical structures is also needed.

Countless articles on pure mathematics begin with the words: “Let us suppose that F is a field with such and such properties”. Therefore, we need to be able to introduce something similar, so that later the system automatically gives us theorems and facts about the field F, in essence, independently creating a full-fledged article devoted to the field F.

So, what do we need to create such a system? Is it possible to create it in principle? There are several components that are necessary for such a system - they are complex and it will take a lot of time to create them. But based on my experience of working on Mathematica , Wolfram | Alpha and A New Kind of Science (a fundamental monograph on cellular automata and related issues - “A New Type of Science”), I am pretty sure that with proper guidance and sufficient effort, they can all be are created.

The key component is the presence of an exact symbolic description of mathematical concepts and structures. Most of it already exists - after more than a quarter of a century of working on it - in the Mathematica system. Therefore, the most abstract ways of representing geometric objects , equations , stochastic processes , quantifiers , etc. are directly embedded into the Wolfram Language . But what is not yet present in Wolfram Language is representations of such concepts of pure mathematics as, for example, bijections, abstract semigroups or Cartesian squares .

Mathematica pura

Over the centuries, many mathematicians studied a variety of problems. But is it possible to expand the Wolfram Language so that it covers the whole range of tasks in pure mathematics and does something like “Mathematica Pura”? Undoubtedly, the answer is yes. solving this problem will be amazingly interesting, but it will require the most complex elaboration of the structure of the language.

I have been developing the structure of such a language for 35 years now - and I can say that this is the most difficult intellectual task of all that I have met. It requires a combination of clear thinking with an aesthetic and pragmatic approach. One constantly has to figure out to achieve the most profound understanding of things and unify everything as much as possible, and the result of the work should always be primitives that represent things in the simplest and most obvious way.

At the moment, the main way to describe pure mathematics (for example, in articles) is a mixture of mathematical notation and natural language along with a small number of schemes. And this should be the starting point when developing an exact symbolic language for pure mathematics.

One might think that one way or another, mathematical notation has already solved this problem, but in fact, there is not such a large number of constructions and concepts that can be expressed in any standardized way using mathematical notation, while many of they are already available in the Wolfram Language.

So how do we move on? The first step is to understand what primitives are needed. The entire Wolfram Language currently contains about 5000 built-in functions along with millions of built-in standardized data objects. It seems to me that for broad support of pure mathematics, we will need about a thousand more additional well-thought functions, probably along with several tens of thousands of new data objects or their analogues, which will complement and link the existing structure.



Consider an area such as functional spaces. Most likely, the FunctionSpace function must exist in this area, defining the function space. Then, operations on functional spaces will be needed, for example, PushForward (the image of a measure under the action of a mapping) or MetrizableQ (whether the space is metrizable). Further, it will be necessary to define a set of known function spaces, for example, “CInfinity” (a space of infinitely differentiable functions) with various parametrization options.

At a low level, it all comes down to symbolic expressions. But in the Wolfram Language, in the end, it all comes down to three ways to directly enter information, all of which are necessary in order to have a convenient and readable language. The first way is to use concise notation - such as + or ∀ - just as in the usual mathematical notation. The second is the use of very carefully crafted function names, for example, MatrixRank or Simplex . And the third is the use of a free input form in natural language, for example, “trefoil knot ” ( triple knot) or “ aleph0 ” (the power of the many aleph-0).

We want to have a short record for some of the most common structural or connecting elements, but we need the right number of them: not too little (as in LISP) and not too much (as in APL). In addition, we want the names of functions to be as if what they are doing is simply written in ordinary words, so that you can easily get an idea of ​​the purpose of the function by simply reading its name by words.

Computers and people

But in the modern world of the Wolfram Language, there is also a free input form in natural language. The key point here is that using it, you can effectively use the whole variety of convenient (albeit ugly) writing options that only real mathematicians understand and use. For example, “L2” may in the appropriate context be interpreted as “Lebeste space of the second degree”. A natural language recognition system will take care of resolving the ambiguity in interpreting such a query and find the canonical symbol form for it.

Ultimately, each construction or concept of pure mathematics, which has its own name, must find its place in our symbolic language: most of the objects from more than 13 thousand articles on the MathWorld website, materials about 5600 elements of the MSC2010 classifier of concepts, all of those objects in any field, the essence of which mathematicians understand immediately, as soon as they hear their name.

Suppose we manage to create an exact symbolic language that works with the concepts of pure mathematics. What can we do with it?

Let's say you can work in the “Wolfram | Alpha style”: you enter something in a free form, the entered data are interpreted by the language, and after all the calculations are done, you will receive a generated report.

But you can also consider this option: if we have such a perfectly thought-out character language, it will be useful not only for computers, but also for humans. In fact, if the language turns out to be good enough, then probably people will begin to write their mathematical calculations on it, instead of the classic mixture of natural language and mathematical notation.

When I program in the Wolfram Language, it often turns out to think right there. I don’t think of what I want to do in a natural language and then translate it into the Wolfram Language. I form thoughts on the Wolfram Language initially and its structure helps me shape these thoughts.

If we manage to develop a fairly good symbolic language for pure mathematics, this, among other things, will give mathematicians a tool that can be used directly in thinking. This is also good because if you can describe what you think in an exact symbolic language, then any ambiguity or ambiguity disappears: in the documentation of the language you can always find a unique description of any object and symbol.

At the same time, as soon as pure mathematics begins to be written down in an exact symbolic language, it becomes what you can do calculations on. Evidence can be generated and verified. You can search for theorems. You can automatically find links and chains of prerequisites.

But well, let's say we just have a computational apparatus necessary for pure mathematics. How can we use it to implement the workflow in the “Wolfram | Alpha style” - when we enter descriptions of things, and automatically get all sorts of mathematical knowledge about them?

There are, apparently, two different ways to solve this issue. The first is to present an abstract listing of possible theorems about the entered data, and then use a heuristic algorithm for selecting those that may be interesting. The second is to start by creating calculated versions of those millions of theorems ever published in the mathematical literature, and then to understand how to find the connection between them and any entered query.

Each of these areas, in fact, reflects a slightly different perspective on how mathematics research is going on. And about every direction there is something to tell.

Mathematics by enumeration

Let's start with a sequence of theorems. In the simplest case, one can begin with a system of axioms and a consistent formulation of correct theorems based on this system. There are two main ways to do this. The first is to formulate hypothetical statements and, using direct or indirect evidence , determine the true ones. The second is to list possible methods of proof , and then find out possible ways of applying axioms.

Both ways are easy to implement if the object is, for example, Boolean algebra. The result will be a sequence of true theorems. But if a person looks at them, many of them will seem trivial or uninteresting. Thus, the question arises which of the theorems are “interesting enough” for them to be included in the generated report.

My first assumption was that such an automatic approach in this matter does not exist, and also that interest in various theorems necessarily depends on the historical development of the corresponding field of mathematics. But when I was working on A New Kind of Science, I did a simple experiment in Boolean algebra.



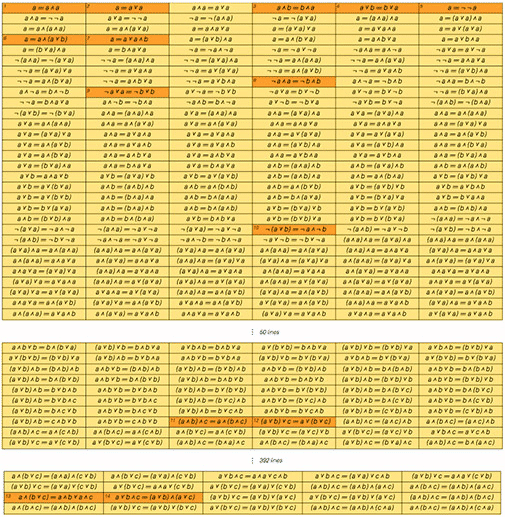
In Boolean algebra there are 14 theorems that are considered “quite interesting” and are given special names in textbooks. I took all possible theorems and listed them in order of complexity (by the number of variables, operators, etc.) and I discovered an amazing thing - the combination of the above theorems mainly refers to those that cannot be proved directly with the previous ones in the list. In other words, the theorems that were given the names are, in a sense, minimal statements that give new information about Boolean algebra.

Boolean algebra is, of course, the simplest example. And besides, in this example of construction, as soon as we obtain theorems that correspond to all axioms, we can conclude that there is no longer any “interesting” theorem, which is quite absurd for many mathematical theories. But I think that this example shows well how one can in fact automatically find out which theorems should be “included in a report”, and which ones are “uninteresting” and are just “decorations” of the report.

Measure of interest

Of course, the problem of classification by interest arises in Wolfram | Alpha all the time. In mathematical examples, these are questions like: “which area of ​​the graph is the most interesting?”, “Which alternative forms of expressions are interesting?”, Etc. Even when someone enters one number, you can ask, “which closed forms of this number are interesting?” - and in order to understand this, it is necessary to classify all types of mathematical objects (for example, how complicated is the representation of π with respect to log (343) and to the Hinchin constant , etc.?)



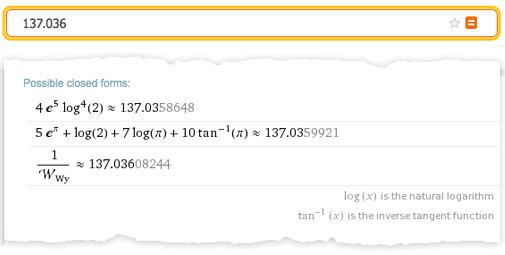
So, in principle, you can imagine a system that generates "interesting" theorems about what goes into the input. Notice that while in normal calculations in Mathematica , data is received at the input and calculations are performed on them “to get an answer”, here interesting statements are generated about them.

The nature of the input is also different. In the case of calculations, you usually deal with the operation to be performed. In the case of working with pure mathematics in the “Wolfram | Alpha style”, the user usually gives a description of some object. In some cases, it is explicit, say: a number of a certain type, a specific equation, a graph of a certain type. But more often it is implicit, for example, it may just be a set of constraints. Say, for the above example with a field, we say: "Let F be a field," and then we set the constraints that this field must satisfy.

In a sense, the axiom system also sets constraints : it does not claim that such an operator “is Nand” (Sheffer's stroke); it is simply stated that the operator must satisfy certain conditions. We know from Gödel's theorem that it is impossible, even for something like standard Peano arithmetic, to completely overcome the restrictions — we can never pin a specific operation, for example, the simple addition of integers, with the “+” sign in axioms. Of course, at the same time we can prove quite a lot of theorems about “+”, including those that we use for the report.

So, with specific input data, we can figure out how to present them as a set of constraints in our exact character language. Then we can formulate theorems based on these constraints and heuristically choose among them the “most interesting” ones.

I am sure that one day this occupation will become the most important part of the work of pure mathematics. Today, for most pure mathematicians, this task will seem alien, since they are not accustomed to the “without the author” theorems; they are accustomed to theorems from articles of concrete mathematicians.

And this leads us to the second approach, to the automatic generation of “mathematical knowledge: start with the entire collection of written mathematical articles, and then associate it with any specific input data. So that you can say, for example, “The following theorem from article X is applicable to your input data in some way”, etc.

Supervising the entire mathematics database

How big is the historical foundation of mathematics? In total, there are about 3 million published mathematical articles, or about 100 million pages, and this number increases by an average of 2 million pages per year. At the same time, all these articles, apparently, contain about 5 million different formulated theorems.

What can you do with this? First of all, of course, simple research and processing. Often the words in the article describe a lot more material than just a mathematical notation and formulations of theorems. But with the help of linguistic recognition technology for mathematical queries in Wolfram | Alpha, it is not so difficult to implement a good statistical processing of a collection of mathematical articles.

But can we go further? Someone might think about creating tags for source documents in order to improve the review. But I believe that such work will not make sense, as indicated by the fact that it is much easier and better for the Internet to create a more refined and conscious system than simply adding tags from each document and their groups.

What would certainly be more rational is to translate the theorems into the original computable form: extract the theorems from the articles and rewrite them in the exact symbolic language.

Is it possible to do this automatically? In the end, I suppose for the most part this will be possible. Today, we can already take small fragments of theorems from the articles and use the Wolfram | Alpha linguistic recognition system to convert them into Wolfram Language code. But gradually it will be possible to move on to large fragments, and in the end to come to the conclusion that to transform a typical theorem into an exact symbolic form, only the smallest effort of a person will be needed.

So let's imagine that we organized all the theorems from mathematical literature in a computable form. What will we do next? We would, of course, be able to build a visual system similar to Wolfram | Alpha, which would be very useful in practice for pure mathematics.

Intractable problems

However, there will inevitably be some limitations that, in fact, the mathematics itself imposes. For example, it is not always easy to say which theorem can be applied to which object and even which theorems are equivalent. In the end, these are classic theoretically unsolvable problems - and I suspect that they will create difficulties in practice. At least, one can apply to them such a basic process as automatic proof.

So, a combination of the two main approaches that we have discussed is proposed. First, the entire collection of published mathematical works is taken and is considered formally as a giant 5-millionth system of axioms, and then follows a procedure for the consistent formulation of theorems, that is, what we called the “listing of interesting facts”

Math: science or art?

So, well, let's say we created such a system. Will she actually solve the key task of finding new truths in pure mathematics, or will she not cope with this?

I think it all depends on what is considered the essence of pure mathematics. Is it science or art? If this is science, then the rapid creation of a larger number of theorems is of course very good. But if it is an art, then it is not the main thing. If work in pure mathematics is viewed with an artistic picture, then the automatic approach will most likely become counterproductive, since the basis of this activity is a form of human self-expression.

This also relates to the role of evidence. For some mathematicians, only the theorem is important: to know whether the statement is true. In fact, the proof is only the fact that there is no error. But for other mathematicians, proof is a key part of the content of mathematics. For them, proof is a story that clarifies mathematical concepts and unites them.

So what happens when we automatically generate evidence? I had one interesting example that I considered 15 years ago when I was working on A New Kind of Science and had already finished work on the simplest axiom system of Boolean algebra (as it turned out, it consists of only one axiom (p◦q) ◦r) ◦ (p◦ ((p◦r) ◦p)) == r). To prove the consistency of the axiom system, I used an automatic theorem-proof system based on equational logic (which is now built into the FullSimplify function). And I included the generated proof in the book:



It contains 343 steps and with a standard font size will take, perhaps, 40 printed pages. And, as it seems to me, it is completely unreadable for a person. - , 81 . , , . , , , .

, , , « ». , , . .

? , , , , . , , . , , , .

, . , , , , — , .

, , , , , , — Wolfram|Alpha Pro. , Wolfram|Alpha, .



, , . , , . Wolfram|Alpha , , “”, , , (« », ).

, , , , , , , . , ? - , . — .

, . , . : , , Wolfram Language, .

, . , “ ”, , Wolfram|Alpha, -. , , — Mathematica Pura, — , .

, “ ”? , , , -. , « », , , , , , “” “”. , WolframTones , , , .

, , , — . , . , , , ( — , ) , . , , , , . , , , , , , .

, , , — . -. . , - , , - , , .

. , , , . , , , . “ ”, , , . — (A New Kind of Science) — , , -, .

“ ”, , , , - , .

, - , , . , ? , , , . , : , , , .

, . ?

. , , ; . 1960- — , Automath — . , 1970- , Mizar, . « », Coq HOL.

: « » . , , - , , .

Wolfram Language , , , . , , , , .

, Mathematica Pura, Wolfram Language, ? Wolfram Language , . . , x . , Wolfram Language — — .

, Mathematica Wolfram Language, «», . , 19 . ? . , , — , , .

, , 20- . , . , , . , — , Wolfram Language , .

, , , . , , , , . , , , , - . — , , , , .

So, what can be said about the curation of theorems from all mathematical literature? Using Wolfram | Alpha and Wolfram Language, not to mention, for example, Wolfram Functions Site and Wolfram Connected Device Project , we already have a lot of experience in creating and maintaining huge databases of structured data on a variety of objects, as well as to make this kind of data computable.

An example of an eCF - chain framing project

But in order to get a clear idea of ​​what the organization and ordering of mathematical theorems is, we have been carrying out our pilot project based on the Wolfram Foundation , supported by the Alfred Sloan Foundation , over the past two years. For this project we have chosen a very specific and well-developed section of mathematics: the study of continued fractions. Chain fractions have been continuously studied since ancient times, but reached a peak of their popularity between 1780 and 1910. In total, they are described in approximately 7,000 books and articles with a total volume of about 150,000 pages.

We selected about 2000 documents, and then proceeded to extract theorems and other mathematical information from them. The work resulted in approximately 600 theorems, 1500 basic formulas and 10,000 derivative formulas. The formulas were presented directly in a computed form, so it was not difficult to attach them to more than 300,000 formulas on the Wolfram Functions website, each of which is now embedded in Wofram | Alpha. But at first we considered theorems simply as objects with certain properties, such as the place of the first publication, the author of the theorem, etc. Moreover, even at this stage, we managed to insert a number of remarkable possibilities into Wolfram | Alpha.



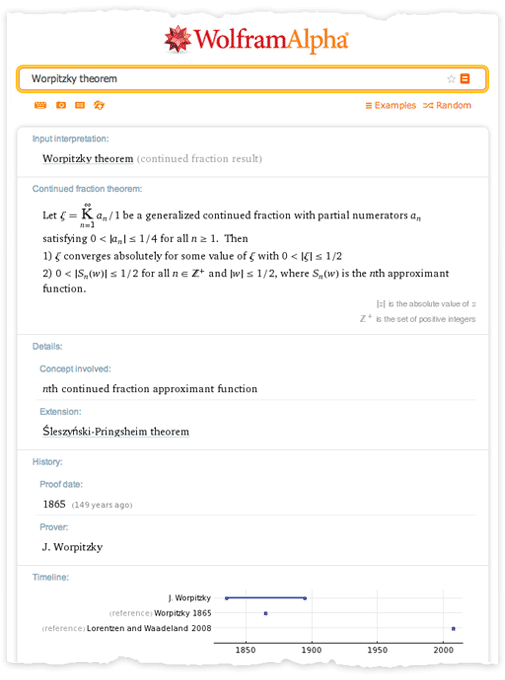
But we also began to try to translate the contents of the theorems into a calculated form. This required the introduction of new designs, such as LebesgueMeasure (Lebesgue measure), ConvergenceSet (many convergence) and LyapunovExponent (Lyapunov exponent). In this case, there were no fundamental problems in creating exact symbolic representations of theorems. Only due to these ideas it became possible to perform similar calculations in Wolfram | Alpha:







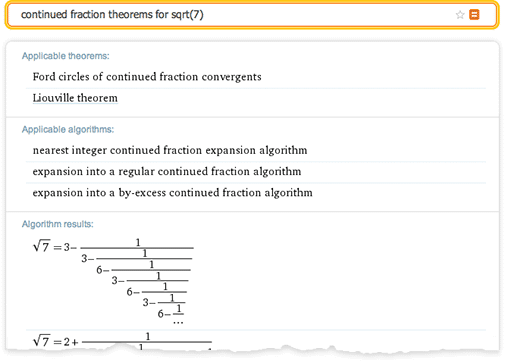
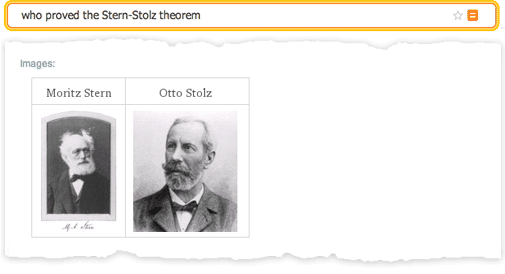
An interesting feature of the project on fractions (abbreviated as “eCF”) was how the process of organizing information actually led to new discoveries in mathematics. Upon completion of the study of more than 50 articles on Rogers and Ramanujan fractions, it became clear that there are cases that they did not take into account that can now be considered. Thus, the results of the calculations filled a gap in this field of research left by Ramanujan, which has not been filled by anyone for over 100 years.



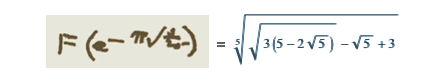
There is always a trade-off between supervising knowledge and creating knowledge from scratch. This is the case, for example, with the Wolfram Functions site, where there has always been a core of relationships between functions found in reference books and other literature. But at the same time, it turned out to be much more efficient to generate and calculate new relationships, rather than combing the literature in their search.



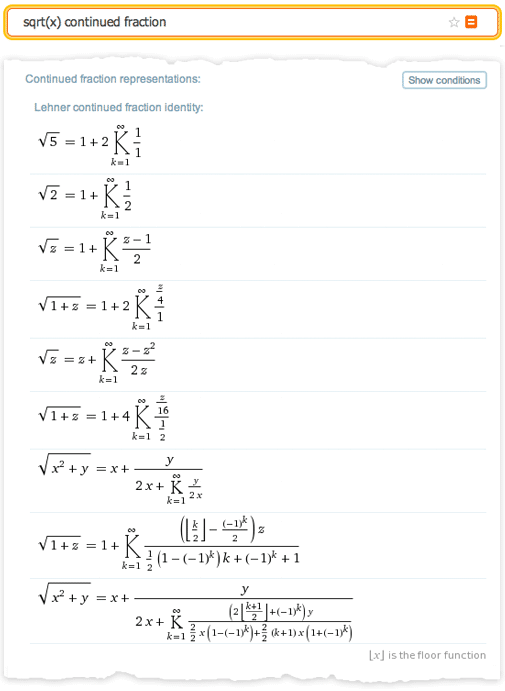
But what is required for the analysis of all mathematical literature, if the goal is to organize and organize knowledge? In the course of this project, the translation of each theorem into a calculated form required about three hours of work by a mathematician. But all this work was done manually, and I’m sure that in a large-scale project, most of the work could be done automatically, not least thanks to the extensions of our natural language recognition system in Wolfram | Alpha.

Of course, in the course of work, all sorts of practical problems arise. New articles are written mainly in TeX, so it is not so difficult to select theorems from them with all the mathematical notation. But older articles need to be scanned, which requires optical recognition systems for mathematical symbols and formulas that are yet to be developed.

Certain difficulties also arise with regard to whether the theorems formulated in the articles are indeed true. And even if the theorem was recognized as valid 100 years ago, it is not known whether it remains so now. For example, in the area of ​​continued fractions, there are many theorems formulated before the 1950s, which were successfully proved at one time, but which did not take into account branch points and the cut line of multi-sheet functions of a complex variable, thus, these days they cannot be considered true .

At the same time, in the end, of course, a lot of good mathematicians are required in order to direct the process of organization and ordering and to translate the theorems into a calculated form. But in a sense, such a mobilization of mathematicians is not out of the ordinary; A similar association of scientists was needed when the mathematical journal Zentralblatt was founded in 1931, or in 1941 at the start of the publication of the journal Mathematical Reviews. (Funny, but the founder and chief editor of both journals was Otto Neugebauer, who worked a little further down the corridor from me at the Institute for Advanced Study in the early 80s, about which I thought he was not engaged in anything other than deciphering Babylonian mathematical works, until until I did some research for this post).

When everything actually comes to creating a system for the system description of pure mathematics, that is an interesting example: the Theorema system, initiated by Bruno Buchberger in 1995, which was recently updated to version 2. Theorema is written in the Wolfram Language and provides an environment like to display mathematical formulations and proofs, and to implement full-fledged computational algorithms for automatic proof of theorems, etc.



Without a doubt, this system will become an element of what will be created in the end. But overall, the project will inevitably be large enough - perhaps this is the world's first example of “big math” (“big math”). So is it possible now to bring this project to completion? The key element is that we now have the technical ability to develop a language and build the necessary infrastructure. But besides this project, a strong interest of the world mathematical community is needed, as is the need for the participation of each individual mathematician from all possible sections of this science. In this case, the reality is that this is probably not the project that could be put on commercial rails, so that about $ 100 million needed for the development of the project should be collected from non-commercial sources.

But this is a serious and important project that promises to be the key for pure mathematics. Each region has its own “golden age” when the main discoveries were made. And most often the beginning of such “golden eras” was the creation of new methodologies or the emergence of new technologies. And this, I am sure, will happen with the field of pure mathematics. If we can direct our efforts to organize and organize mathematical knowledge and build a system that will use them and create calculated forms of knowledge based on them, then we will succeed not only in preserving and spreading the vast legacy of pure mathematics, but also give impetus to the rapid growth of this section of science.

Large projects like this need reliable guidance. And I am always ready to do my part of the work and bring in the basic technologies that will be required for its implementation. Now for the further development of the project requires the interest of the entire global mathematical community. We have the opportunity to make the second decade of the twentieth century a truly significant period in the entire millennial history of pure mathematics. So let's do it!