Two beautiful tasks on algorithms
This week I started to read a basic course on algorithms for bachelors of the Academic University. I started completely from the basics, and so that those who are already familiar with the basic algorithms have something to do, I at the beginning of the pair formulated two, probably my most favorite algorithms tasks. Let's share them with you. The solution of one of them even under the cut will tell in detail. But do not deny yourself the pleasure and do not look immediately under the cat, but try to solve the problems yourself. I promise that both tasks have fairly simple solutions that do not imply any special knowledge of the algorithms. This, of course, does not mean that these solutions are easy to find, but after a couple one of the students came up and told the correct solution to the first task. =) If you are interested in looking at the beginning of the course or solving more different tasks, come to us for the (free) online course , which will begin on September 15th.
Immediately explain. The condition does not say that every number from 1 to n occurs in an array, so there can be as many repeated elements as there were (if all the numbers came in once and one thing twice, the task would be much simpler). The restriction on the use of additional memory means that you can not start an additional array of linear length, but you can wind up variables.
')
The local minimum of a matrix is an element that is smaller than all its four neighbors (or three, if this element lies on the boundary; or two, if it is a corner element). Please note that we are required to have time linear for n, although the number of elements in the matrix is quadratic in n. Therefore, we assume that the matrix is already read into memory. And we need to find a local minimum in it, referring only to the linear number of its cells.
Under the cut - the solution to the first problem. Once again I urge you to look under the cat only after you solve the task. For the second task, I can say some hint.
I will try to tell not only the decision, but also the way it could be guessed. I will explain immediately with an example. From it, I hope, it will be clear how the algorithm works in the general case. Working example:

That is, we are given an array of length 9 containing numbers from 1 to 8, and our goal is to find a two or a five.
As we remember, the use of additional memory in the condition of the problem is prohibited. Let us, however, understand how she could help us. We would then have introduced a new array of size n and in one pass through the original array A would count how many times each of the numbers from 1 to n goes into A. From this array it would be immediately obvious who in A repeats.

This will not help us in the future, but still.
The restriction on additional memory does not allow us to collect and record supporting information about the array. So, we need to find a repeating element, somehow “walking” through the array. Walking through the array can be from left to right, for example, but it is unclear what information can be extracted. Therefore, we will try to walk differently. Let us stand in the first element of our array and see what is written there. The number 7 is written there, so let's look at the seventh element of the array. The number 1 is written there. The walk turned out to be short, we were fixated. The fact that there are some cycles in the array will help us a lot in the future. For example, let's also try to walk from the second element: from there we go to element number 5, from it to element number 3, and from element number 3 we return again to element number 2. That is, we found another cycle. Let's draw the two cycles we found:
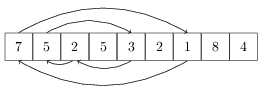
And since we realized that our array implicitly defines some graph, then let's draw this graph explicitly. Formally, the vertices of the graph are numbers from 1 to n + 1; we draw an oriented edge from i to j if A [i] = j.

We are interested in vertices in this graph, which include at least two edges (if edges j come from vertices i and k, then A [i] = A [k] = j, that is, j is repeated in array A). It is clear to us that there is such a vertex in the graph, but let us realize this once again, in terms of graphs. In our graph, exactly one edge comes out of each vertex (and therefore, there is an edge in the graph (n + 1)), but there is one vertex into which nothing enters: this is the vertex (n + 1). Hence, there is a vertex, which includes at least two edges. In general, this was already clear, but a remark about the vertex (n + 1) will help us in the future.
Let's stand at the vertex (n + 1) and move in our graph along the outgoing edges. Someday we will get stuck, of course, but what’s important is that we won’t go back to the vertex (n + 1). In our working example, we will exit vertex 9 and get to the cycle (5,2,3). It can be seen that the entry point to this cycle is the repeating element: after all, it is possible to enter this point and along the edge of the cycle, and along the edge on the way from the vertex (n + 1) to the cycle. In our example, such an entry point is a vertex 5.
Finding this point is a separate, not too simple task, but its solution is very similar to solving the standard list obsession problem. The cycle length is easy to find. For example, let's make n + 1 step from vertex n + 1. After that, we will definitely be at the top of the loop. Remember this peak and we will continue to walk until we return to it. Thus, we find the cycle length k. Now we do the following. Put two pointers to the vertex n + 1. The first pointer is k steps. After that, we will move each of the pointers one step forward until they meet (thus, the first pointer will always overtake the second by k steps). It is clear that these guys will meet just at the point of entry we need. In our example, the cycle length is three. After three steps, the first pointer will be at the top 2. At this point we will start moving the second pointer. In two steps, the pointers will meet at the top 5.
For a snack. We did not discuss why it was forbidden to modify the array (and our array did not really touch the array). Think of a simpler solution if you are allowed to spoil the array.
Problem 1. Given an array A of length (n + 1), containing natural numbers from 1 to n. Find any duplicate element in O (n) time without changing the array and without using additional memory.
Immediately explain. The condition does not say that every number from 1 to n occurs in an array, so there can be as many repeated elements as there were (if all the numbers came in once and one thing twice, the task would be much simpler). The restriction on the use of additional memory means that you can not start an additional array of linear length, but you can wind up variables.
')
Problem 2. Given a matrix nxn containing pairwise distinct natural numbers. It is required to find a local minimum in it during the time O (n).
The local minimum of a matrix is an element that is smaller than all its four neighbors (or three, if this element lies on the boundary; or two, if it is a corner element). Please note that we are required to have time linear for n, although the number of elements in the matrix is quadratic in n. Therefore, we assume that the matrix is already read into memory. And we need to find a local minimum in it, referring only to the linear number of its cells.
Under the cut - the solution to the first problem. Once again I urge you to look under the cat only after you solve the task. For the second task, I can say some hint.
I will try to tell not only the decision, but also the way it could be guessed. I will explain immediately with an example. From it, I hope, it will be clear how the algorithm works in the general case. Working example:

That is, we are given an array of length 9 containing numbers from 1 to 8, and our goal is to find a two or a five.
As we remember, the use of additional memory in the condition of the problem is prohibited. Let us, however, understand how she could help us. We would then have introduced a new array of size n and in one pass through the original array A would count how many times each of the numbers from 1 to n goes into A. From this array it would be immediately obvious who in A repeats.

This will not help us in the future, but still.
The restriction on additional memory does not allow us to collect and record supporting information about the array. So, we need to find a repeating element, somehow “walking” through the array. Walking through the array can be from left to right, for example, but it is unclear what information can be extracted. Therefore, we will try to walk differently. Let us stand in the first element of our array and see what is written there. The number 7 is written there, so let's look at the seventh element of the array. The number 1 is written there. The walk turned out to be short, we were fixated. The fact that there are some cycles in the array will help us a lot in the future. For example, let's also try to walk from the second element: from there we go to element number 5, from it to element number 3, and from element number 3 we return again to element number 2. That is, we found another cycle. Let's draw the two cycles we found:

And since we realized that our array implicitly defines some graph, then let's draw this graph explicitly. Formally, the vertices of the graph are numbers from 1 to n + 1; we draw an oriented edge from i to j if A [i] = j.

We are interested in vertices in this graph, which include at least two edges (if edges j come from vertices i and k, then A [i] = A [k] = j, that is, j is repeated in array A). It is clear to us that there is such a vertex in the graph, but let us realize this once again, in terms of graphs. In our graph, exactly one edge comes out of each vertex (and therefore, there is an edge in the graph (n + 1)), but there is one vertex into which nothing enters: this is the vertex (n + 1). Hence, there is a vertex, which includes at least two edges. In general, this was already clear, but a remark about the vertex (n + 1) will help us in the future.
Let's stand at the vertex (n + 1) and move in our graph along the outgoing edges. Someday we will get stuck, of course, but what’s important is that we won’t go back to the vertex (n + 1). In our working example, we will exit vertex 9 and get to the cycle (5,2,3). It can be seen that the entry point to this cycle is the repeating element: after all, it is possible to enter this point and along the edge of the cycle, and along the edge on the way from the vertex (n + 1) to the cycle. In our example, such an entry point is a vertex 5.
Finding this point is a separate, not too simple task, but its solution is very similar to solving the standard list obsession problem. The cycle length is easy to find. For example, let's make n + 1 step from vertex n + 1. After that, we will definitely be at the top of the loop. Remember this peak and we will continue to walk until we return to it. Thus, we find the cycle length k. Now we do the following. Put two pointers to the vertex n + 1. The first pointer is k steps. After that, we will move each of the pointers one step forward until they meet (thus, the first pointer will always overtake the second by k steps). It is clear that these guys will meet just at the point of entry we need. In our example, the cycle length is three. After three steps, the first pointer will be at the top 2. At this point we will start moving the second pointer. In two steps, the pointers will meet at the top 5.
For a snack. We did not discuss why it was forbidden to modify the array (and our array did not really touch the array). Think of a simpler solution if you are allowed to spoil the array.
Source: https://habr.com/ru/post/235855/
All Articles