Data mining. Optimization of orders for goods in the pharmacy (pharmacy)
In a small pharmacy there is a need for a flexible ordering system for medicines and para-pharmaceutical products sensitive to constant market fluctuations. Within the framework of the current reality, single pharmacies do not have sufficient storage facilities (material rooms), which leaves its mark and forces the person responsible for orders to make them daily from the consolidated price list for several suppliers, avoiding duplication, at minimal prices, excluding goods with inappropriate expiration dates. In this case, the total nomenclature is several tens of thousands of units.
We live in the modern world, where the computer performs routine operations for us. Therefore, you can say: "Let's use a computer, and he will do all the hard work for us!" “Do you have a database containing statistics on sales of various drugs?” You continue - “So why not use these statistics to forecast sales and create an automatic application for the required drugs?”
Yes, in the first approximation, you will be right. Such solutions are in software complexes that automate pharmacies in Russia. But there is one very big "BUT". All these solutions will not work correctly until you create groups of products.
I will explain: There is a drug: “Donormil 15mg Tab. X30 "production Upsa Laboratoir France and Donormil tab. 15 mg № 30 Aventis / Bristol-Myers Squibb - France. In the database, they are completely two different drugs with a different identifier and a different name, but this is the same thing. If you take into account statistics on these two different products, then you will not get the correct result.
')
In order to obtain reliable information on the movement and the need to order a product, it is necessary to create groups of identical goods. As a rule, you need to create groups manually and process a large number of records. If there is a dedicated employee who can work for a long time on filling the reference book of the “Product Group”, then this is more or less realistic (however, it should be borne in mind that when new goods arrive, the directory needs to be constantly updated). Within a small pharmacy, where two or three people usually work behind the counter, there is simply no such possibility.
The question arises: "What are the algorithms that allow you to find the same drugs?" The first thing that comes to mind is the calculation of the Levenshtein distance. But here we are confronted with the restriction of this algorithm - the Levenshtein distance for various goods “Linex caps. x16 "and" Linex caps. x32 "(the distance is two), less than the same goods" Linex caps. x16 "and" Linex N16 caps "(the distance is nine). The problem is that suppliers can change words in places, replace reductions in quantity (someone writes No., someone N, someone X), volume, etc. Combining the same goods using a bar code is not possible. The same products made by different factories have a different bar code. Moreover, the same product, produced at one plant, may have a different bar code after passing re-registration.
After a long search, I came to the following algorithm for finding the same drugs:
1. For the first approximation (search for "similar" drugs), the N-Gram algorithm is used. This algorithm makes up all possible combinations of substrings, with a length of up to the specified one, and counts their matches. The number of matches divided by the number of variants is declared by the coefficient of similarity of lines for a fixed N (I chose the value 3) and is given as the result of the function.
For example, for Linex Caps N16 and Linex N16 Caps, the lines are broken down into 3-grams:
The result is 0.88.
Thus, we combine drugs for which the keywords are swapped. However, this algorithm has two drawbacks:
a) The algorithm combines drugs with "x10" and "x20", "g." and "mg.", etc .;
b) The load on the database increases dramatically - a gram dictionary occupies a very large volume. For example, for a reference book of inventory holdings of approximately 30 thousand entries, the 3-gram dictionary contains 900 thousand entries. For a price of 47 thousand entries (combined price from several suppliers), the dictionary already contains 1.7 million entries.
2. For the final filling of the directory “Groups of goods” (after which a person’s work is required) the source reference book of material values ​​is broken down into a dictionary of words. A meta-directory of “key” drug properties is created:
a) Volume;
b) Quantity;
c) Amount of active substance;
d) Medicinal substance;
e) Color, taste;
etc.
Meta-reference book contains data on synonyms, correspondences (for example: r = 1000 mg) and the method of searching properties in the dictionary. Eliminating among the "similar" drugs (the result of the first algorithm) drugs for which the "key" properties are different, we get the reference "Groups of goods".
The specified algorithm allows you to automatically fill in the reference book of the “Product Group”, which is later edited by the user.
The next question I had to decide was the question "which prediction algorithm" to use? Since I did not want to use complex and resource-intensive algorithms and, besides, the pharmacy works only for the first year (there is no seasonality), I chose the Dual Exponential Smoothing algorithm.
Formulas look like this:
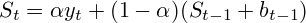
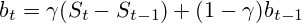
Where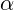
and 
take values ​​from the range [0; 1]
y is the real number of sales;
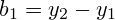
To predict the following value, the formula is used:
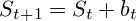
To predict multiple values:
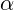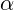As we see, to calculate the forecast, you need to know the value of two variables - and . Optimal values and is selected from the minimum of the square error of the forecast (the sum of the squares of the difference in the number of actually sold goods and the forecast). Thus, we are faced with the classical problem of finding the minimum of a function of several variables with linear constraints.
At school, when I first studied Fortram, Dad bought J. Forsyth's book, Machine Methods of Mathematical Computing. I remember my surprise from the first acquaintance with the floating-point calculation, the concept of "Machine Epsilon". Remembering this book, I found a minimum search algorithm in it, but only for the function of one variable. For the function of several variables, the author sent the reader to the unfinished (1977, at the time of writing) book MINPACK from the National Laboratory in Argon. Imagine my surprise when I found this package written in Fortran, found the MINPACK C / C ++ package, and spoke with the author of the “translation” from Fortran to C.
To date, for the forecast sales of drugs, I have implemented a software package consisting of:
a) Libraries for MS SQL Server (dll), implemented as extended stored procedures, written in C ++ and implementing the forecast calculation;
b) MS SQL Server databases containing dictionaries, metadata and stored procedures: calculating the forecast, comparing inventory values ​​and price list, and others.
c) The client, in which the user makes a forecast, works with reference books and price lists.
The introduction of the software complex has accelerated the work on the order of goods and increased the efficiency of the pharmacy. And more importantly - returned the wife to the family!
The software complex I implemented is tightly tied to one vendor that automates the pharmacy business in Russia. Using the versatility of the approach, you can implement a similar solution for other software products. This algorithm can be applied not only in the pharmacy business, but also in any other where there is a large range of goods of the same type, and there is a need to combine a directory of inventory items and sales forecast in the face of fierce competition and constant changes in the market.
We live in the modern world, where the computer performs routine operations for us. Therefore, you can say: "Let's use a computer, and he will do all the hard work for us!" “Do you have a database containing statistics on sales of various drugs?” You continue - “So why not use these statistics to forecast sales and create an automatic application for the required drugs?”
Yes, in the first approximation, you will be right. Such solutions are in software complexes that automate pharmacies in Russia. But there is one very big "BUT". All these solutions will not work correctly until you create groups of products.
I will explain: There is a drug: “Donormil 15mg Tab. X30 "production Upsa Laboratoir France and Donormil tab. 15 mg № 30 Aventis / Bristol-Myers Squibb - France. In the database, they are completely two different drugs with a different identifier and a different name, but this is the same thing. If you take into account statistics on these two different products, then you will not get the correct result.
')
In order to obtain reliable information on the movement and the need to order a product, it is necessary to create groups of identical goods. As a rule, you need to create groups manually and process a large number of records. If there is a dedicated employee who can work for a long time on filling the reference book of the “Product Group”, then this is more or less realistic (however, it should be borne in mind that when new goods arrive, the directory needs to be constantly updated). Within a small pharmacy, where two or three people usually work behind the counter, there is simply no such possibility.
The question arises: "What are the algorithms that allow you to find the same drugs?" The first thing that comes to mind is the calculation of the Levenshtein distance. But here we are confronted with the restriction of this algorithm - the Levenshtein distance for various goods “Linex caps. x16 "and" Linex caps. x32 "(the distance is two), less than the same goods" Linex caps. x16 "and" Linex N16 caps "(the distance is nine). The problem is that suppliers can change words in places, replace reductions in quantity (someone writes No., someone N, someone X), volume, etc. Combining the same goods using a bar code is not possible. The same products made by different factories have a different bar code. Moreover, the same product, produced at one plant, may have a different bar code after passing re-registration.
After a long search, I came to the following algorithm for finding the same drugs:
1. For the first approximation (search for "similar" drugs), the N-Gram algorithm is used. This algorithm makes up all possible combinations of substrings, with a length of up to the specified one, and counts their matches. The number of matches divided by the number of variants is declared by the coefficient of similarity of lines for a fixed N (I chose the value 3) and is given as the result of the function.
For example, for Linex Caps N16 and Linex N16 Caps, the lines are broken down into 3-grams:
| Compare string | Second string substrings | Matches | Number of matches | Number of options | Similarity coefficient |
|---|---|---|---|---|---|
| Ling | Lin, ine, nek, ex, ks, with N, N1, N16,16, 6 k, ka, cap, aps | Yes | |||
| ine | Lin, ine, nek, ex, ks, with N, N1, N16,16, 6 k, ka, cap, aps | Yes | |||
| some | Lin, ine, nek, ex, ks, with N, N1, N16,16, 6 k, ka, cap, aps | Yes | |||
| ex | Lin, ine, nek, ex, ks, with N, N1, N16,16, 6 k, ka, cap, aps | Yes | |||
| cc | Lin, ine, nek, ex, ks, with N, N1, N16,16, 6 k, ka, cap, aps | Yes | eleven | 13 | |
| with to | Lin, ine, nek, ex, ks, with N, N1, N16,16, 6 k, ka, cap, aps | Not | |||
| ka | Lin, ine, nek, ex, ks, with N, N1, N16,16, 6 k, ka, cap, aps | Yes | |||
| cap | Lin, ine, nek, ex, ks, with N, N1, N16,16, 6 k, ka, cap, aps | Yes | |||
| aps | Lin, ine, nek, ex, ks, with N, N1, N16,16, 6 k, ka, cap, aps | Yes | |||
| ps | Lin, ine, nek, ex, ks, with N, N1, N16,16, 6 k, ka, cap, aps | Not | |||
| with N | Lin, ine, nek, ex, ks, with N, N1, N16,16, 6 k, ka, cap, aps | Yes | |||
| N1 | Lin, ine, nek, ex, ks, with N, N1, N16,16, 6 k, ka, cap, aps | Yes | |||
| N16 | Lin, ine, nek, ex, ks, with N, N1, N16,16, 6 k, ka, cap, aps | Yes | |||
| (11 + 12) / (13 + 13) = 0.88 | |||||
| Ling | Lin, ine, nek, ex, kc, with to, ka, cap, aps, ps, with N, N1, N16 | Yes | |||
| ine | Lin, ine, nek, ex, kc, with to, ka, cap, aps, ps, with N, N1, N16 | Yes | |||
| some | Lin, ine, nek, ex, kc, with to, ka, cap, aps, ps, with N, N1, N16 | Yes | |||
| ex | Lin, ine, nek, ex, kc, with to, ka, cap, aps, ps, with N, N1, N16 | Yes | |||
| cc | Lin, ine, nek, ex, kc, with to, ka, cap, aps, ps, with N, N1, N16 | Yes | |||
| with N | Lin, ine, nek, ex, kc, with to, ka, cap, aps, ps, with N, N1, N16 | Yes | |||
| N1 | Lin, ine, nek, ex, kc, with to, ka, cap, aps, ps, with N, N1, N16 | Yes | 12 | 13 | |
| N16 | Lin, ine, nek, ex, kc, with to, ka, cap, aps, ps, with N, N1, N16 | Yes | |||
| sixteen | Lin, ine, nek, ex, kc, with to, ka, cap, aps, ps, with N, N1, N16 | Yes | |||
| 6 to | Lin, ine, nek, ex, kc, with to, ka, cap, aps, ps, with N, N1, N16 | Not | |||
| ka | Lin, ine, nek, ex, kc, with to, ka, cap, aps, ps, with N, N1, N16 | Yes | |||
| cap | Lin, ine, nek, ex, kc, with to, ka, cap, aps, ps, with N, N1, N16 | Yes | |||
| aps | Lin, ine, nek, ex, kc, with to, ka, cap, aps, ps, with N, N1, N16 | Yes |
The result is 0.88.
Thus, we combine drugs for which the keywords are swapped. However, this algorithm has two drawbacks:
a) The algorithm combines drugs with "x10" and "x20", "g." and "mg.", etc .;
b) The load on the database increases dramatically - a gram dictionary occupies a very large volume. For example, for a reference book of inventory holdings of approximately 30 thousand entries, the 3-gram dictionary contains 900 thousand entries. For a price of 47 thousand entries (combined price from several suppliers), the dictionary already contains 1.7 million entries.
2. For the final filling of the directory “Groups of goods” (after which a person’s work is required) the source reference book of material values ​​is broken down into a dictionary of words. A meta-directory of “key” drug properties is created:
a) Volume;
b) Quantity;
c) Amount of active substance;
d) Medicinal substance;
e) Color, taste;
etc.
Meta-reference book contains data on synonyms, correspondences (for example: r = 1000 mg) and the method of searching properties in the dictionary. Eliminating among the "similar" drugs (the result of the first algorithm) drugs for which the "key" properties are different, we get the reference "Groups of goods".
The specified algorithm allows you to automatically fill in the reference book of the “Product Group”, which is later edited by the user.
The next question I had to decide was the question "which prediction algorithm" to use? Since I did not want to use complex and resource-intensive algorithms and, besides, the pharmacy works only for the first year (there is no seasonality), I chose the Dual Exponential Smoothing algorithm.
Formulas look like this:
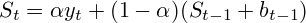
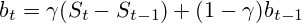
Where
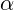and take values ​​from the range [0; 1]
y is the real number of sales;
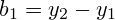
To predict the following value, the formula is used:
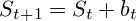
To predict multiple values:
As we see, to calculate the forecast, you need to know the value of two variables -
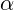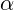and . Optimal values and is selected from the minimum of the square error of the forecast (the sum of the squares of the difference in the number of actually sold goods and the forecast). Thus, we are faced with the classical problem of finding the minimum of a function of several variables with linear constraints.
At school, when I first studied Fortram, Dad bought J. Forsyth's book, Machine Methods of Mathematical Computing. I remember my surprise from the first acquaintance with the floating-point calculation, the concept of "Machine Epsilon". Remembering this book, I found a minimum search algorithm in it, but only for the function of one variable. For the function of several variables, the author sent the reader to the unfinished (1977, at the time of writing) book MINPACK from the National Laboratory in Argon. Imagine my surprise when I found this package written in Fortran, found the MINPACK C / C ++ package, and spoke with the author of the “translation” from Fortran to C.
To date, for the forecast sales of drugs, I have implemented a software package consisting of:
a) Libraries for MS SQL Server (dll), implemented as extended stored procedures, written in C ++ and implementing the forecast calculation;
b) MS SQL Server databases containing dictionaries, metadata and stored procedures: calculating the forecast, comparing inventory values ​​and price list, and others.
c) The client, in which the user makes a forecast, works with reference books and price lists.
The introduction of the software complex has accelerated the work on the order of goods and increased the efficiency of the pharmacy. And more importantly - returned the wife to the family!
The software complex I implemented is tightly tied to one vendor that automates the pharmacy business in Russia. Using the versatility of the approach, you can implement a similar solution for other software products. This algorithm can be applied not only in the pharmacy business, but also in any other where there is a large range of goods of the same type, and there is a need to combine a directory of inventory items and sales forecast in the face of fierce competition and constant changes in the market.
Source: https://habr.com/ru/post/234723/
All Articles