Anatomy of Melancholia

Knowledge is power.

Francis Bacon.

... in much wisdom much sorrow;
and who multiplies knowledge, multiplies sorrow.
')
Book of Ecclesiastes.

Games live their lives. They arise from nowhere, develop, generate new games, are forgotten by everyone and, sometimes, come back from oblivion. There are many examples in the history of games that were defeated in this process of natural selection. These are the various variants of Shogi , which have survived to this day only thanks to the reverent attitude of the Japanese people to their cultural heritage. A party to a game similar to Taikyoku shogi could drag on for months (if not for years). But these chess dinosaurs of the Heian epoch are not the brightest representatives of the fossil world of board games.

I want to talk about a truly amazing game. The threats in it are not obvious, and the goals are not trivial. You can win in many ways, but playing is not easy at all. It can not be attributed either to the Checkers family or to the chess family. Its origin is foggy. For the average man in the street, this game is about as exciting as it is drawing up magic squares . It fully justifies one of its names - only philosophers can play it.

For the first time, the Rithmomachia , also known as the “Battle of Numbers” or “The Game of the Philosophers”, was described, approximately, in 1030 by a monk named Asilo. Authorship, apparently baseless, is attributed to Plato , and the rules of the game are based on Boethius' arithmetic theory. Subsequently, the rules of the game were marginally changed by another monk, named Hermannus Contractus , who added notes on the theory of music. For a long time, Ritmomachia was used as a teaching tool in teaching students to mathematics. Intellectuals of that time played Ritmomachia for pleasure (at one time it was even more popular than Chess), Robert Burton mentioned it in Anatomy of Melancholy , and Thomas More considered this game a good leisure for the inhabitants of his Utopia . Then, suddenly, it was all over. The interests of mathematics and Ritmomachia diverged and the game was forgotten. Of course, this does not mean that we can not remember it.

Rules of the game

Two players play Ritmomachia on a rectangular 8x16 square board. Turns are performed alternately. For each move, one piece moves. As a result of a move, one or more opponent pieces may be taken (removed from the board). The following types of shapes are defined:

• A circle
• Triangle
• Square
• Pyramid

Ignoring the numerical marks on the figures (I’ll talk about them below), you can see that two types of moves are allowed. In the first case, the figure moves in a straight line and can be stopped by any other figure (one’s own or an opponent) on the way. Thus the Circle (one cell diagonally), as well as the Triangle (strictly two cells orthogonal) and Square (strictly three cells orthogonal) are moved. Another possibility is to “jump” the pieces to the target cell, similar to the knight's move in chess. So can walk the Triangle or Square. Any move should be performed only on an empty square.

A unique figure is the Pyramid. Actually it is not a figure, but a set of figures. Each piece in the set (Circle, Triangle or Square) allows the Pyramid to perform the appropriate type of turn. The figure above shows the possible moves of the Pyramid in the "top of the range". As it is easy to guess, by the end of the game, the “completeness” can be greatly disturbed (by the way, the Pythmid from Ritmomachia is the only figure I know that can be “killed in parts”).

I will dwell on the methods of "murder". There are four of them in Ritmomachia:

• Capture by Siege
• Capture by Equality
• Capture by Ambush
• Capture by Eruption

The most radical is the capture of the figure "under siege." The figure will be removed if after the next turn it turns out to be blocked in all diagonal or orthogonal directions. If the figure is located at the edge of the board or in the corner - you will have to block fewer directions. This is the simplest (but not the only) way to take the Pyramid all at once - entirely. Taking “under siege” is the only way that does not use the numerical values ​​of the figures.

Another way is to take a figure with a matching numeric value. If, after completing the move, on the field, where the next move could move the figure (if this field was empty, of course) is the figure of the enemy, with the same numerical value, it will be taken. It should be noted that this method of combat may be asymmetric. So (in the picture above), after White’s move, the Circle, with a numerical value of 16, can take a black Triangle with the same value, but the Triangle, on its own turn, cannot do this, since it goes to other cells. At the same time, white and black triangles with numerical values ​​of 25 beat each other symmetrically (which figure will be taken is determined by the order of the turn).

An improved version of the previous one is the following method. This time, “from ambush”, two figures are attacking. If the sum, difference, product or quotient of their numerical values ​​coincide with the numerical value on the opponent's figure - the figure is removed. This is the most frequently used possibility of fighting figures in the game, but it may be far from easy to see all such threats in a less complex position.

The latter method allows you to beat the pieces in the far distance. If the result of the product or the particular numerical value of the figure and the distance to the opponent’s figure (orthogonal) coincides with the numerical value of the opponent’s figure - the figure is removed. Other figures located in the direction of the battle, do not prevent the threat. When calculating the distance, the starting and ending positions are taken into account. This is a symmetric method of combat (since it does not depend on the rules for moving figures). The sequence of the turn determines which of the pieces will be shot.

It remains to talk about how these rules apply to the Pyramids. With this, everything is simple - in any calculations for taking figures, the Pyramid can act either as an independent figure (its numerical value coincides with the sum of the numerical values ​​of all its components), or as any of its parts. Similarly, the Pyramid can be taken as a whole (by its total value) or in parts (each of its components is vulnerable separately). Given the rules for moving the Pyramid, which I mentioned above, this makes the Pyramid the strongest (and most vulnerable) figure.



The initial placement of figures is associated with another important feature of the game. Although the set of figures is the same, the numerical values ​​differ. Also, the “equipment” of the pyramids is different (shown on the side of the board, for each of the players). This makes the game asymmetric. Tactics and strategies, for the black player are not suitable for white (and vice versa). This makes the game more interesting.

Glorious victories

The rules described above are enough to start playing Ritmomachia, but if the goal of the game was to simply capture all the pieces of the opponent, the game would not be so interesting. Yes, you can win in this way, but this is not the only (and not the best) way to win! I really like the game, the purpose of which is not the straightforward "killing" of enemy figures. So in Chess, to win, it is not at all necessary to “eat” all the figures, it’s enough to checkmate the King! In some versions of Hasami Shogi , the goal of the game is even more unexpected (to win, you need to build a line of 5 of your chips in a row). Ritmomachia does not disappoint in this regard. Here is a list of ways to win in this game (in order of increasing their "gloriousness"):

• De Corpore ("by body"): Take a given (or more) number of enemy pieces (usually 15)
• De Bonis ("by goods"): Take the opponent's pieces with a given (or large) total value (usually 1315 for whites and 984 for blacks)
• De Lite ("by lawsuit"): Take enemy pieces with a given (or large) total value, provided that the number of digits on the captured pieces does not exceed the specified
• De Honore ("by honor"): Take enemy pieces with a given (or large) total value, provided that the number of captured figures does not exceed the specified
• De Honore Liteque ("by honor and lawsuit"): Take enemy pieces with a given (or more) total value, provided that the number of captured pieces does not exceed the set and the number of digits on the captured pieces does not exceed the set
• Victoria Magna ("great victory"): Arrange three figures (on the territory of the enemy) in an arithmetic progression
• Victoria Major (“greater victory”): Arrange four figures (on the enemy’s territory) so that they have two (but not more) groups of three figures placed in different types of progression ( arithmetic , geometric or harmonic )
• Victoria Excellentissima ("most excellent victory"): Arrange (on the territory of the enemy) four figures so that there are all three types of progression

Here you can distinguish between two fundamentally different types of game objectives. Common Victories are associated with the capture of enemy pieces (with the possible limitation of the number of captured pieces, in order to protect against aggressive play). Proper Victories are considered a more worthy conclusion and are associated with the re-creation of a certain “harmony” on the territory of the enemy (which does not exclude the possibility of a battle of enemy figures).



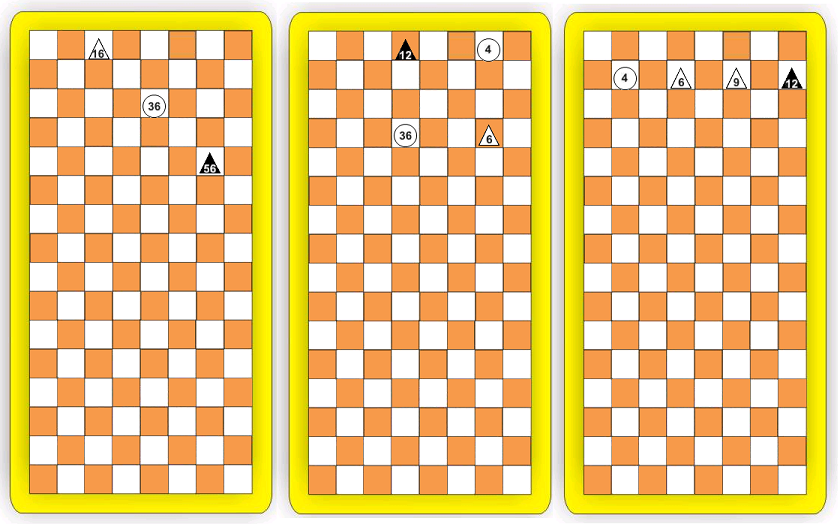
The examples above illustrate that enemy figures can (and should) be involved in “harmony”. In the first case, an arithmetic progression was constructed (16, 36, 56). The second example combines geometric (4, 12, 36) and harmonic (4, 6, 12) progression. In the third case, there are all three types of progression (you can find them yourself). In case there are difficulties with an oral account, tables of all possible solutions in Ritmomachia are built (however, people who have problems with an oral account are unlikely to be interested in Rhythmomachia).

Possible options

In its heyday, ritmomachia has already undergone many changes. Subsequent renovations did not improve the situation. There are many discrepancies in the descriptions of the rules of this game. Some sources give alternative versions of the original arrangement of pieces (I even came across a variant describing the game on a 8 x 14 board):



There are options with simplified rules for moving figures. According to these rules, the figures move in a straight line (orthogonal and diagonal) for a given number of cells. Any figure in the path of movement stops moving. Jumps, like the course of the Horse in Chess, are absent. The pyramid, as usual, combines the moves present in its set of figures.



In addition, there is a variant with the usual rules of the movement of figures, in which a special move of the Pyramid of 3 cells along the diagonal is added. Such a move is possible under the condition that none of the figures originally included in the Pyramid were taken. Another option is associated with the preservation of the initial set of figures of the Pyramid. It is allowed to use the total value of the Pyramid, only under the condition that none of its figures have yet been “eaten”. There are more simple options in which the Pyramid is removed completely if any of its components is attacked.

Some of the options associated with changes in the rules of taking figures. So, in one of the options, to capture a " by Siege " figure (siege), it is necessary to block all directions of its "natural" movement. At the same time, it is not necessary to place your pieces close to the blocked one (the examples below illustrate the concept). This is quite an interesting rule.



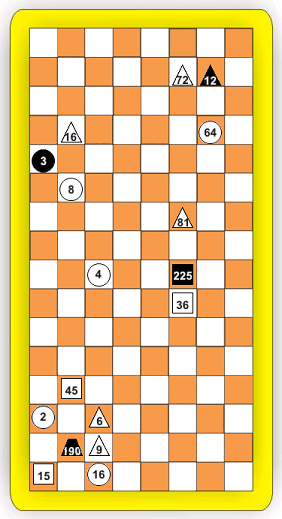
There is an option in which the capture of " by Ambush " (ambush) is carried out like games of a "clamping" type (in this case, the rules for moving figures are ignored):



There are a large number of discrepancies in the definitions of " Glorious Victories ". Often, the conditions of such victories include the preliminary destruction of the enemy's Pyramid. Also, there is a condition for completing the game, limited to taking the Pyramid. There are many variations of this game. Acquaintance with the nuances of the rules, before the start of the game, in any case, is not at all superfluous.

Details for the curious

The implementation of the game is naturally divided into several stages. The easiest way was to realize the movement of figures. From this I started. Here is how the squares look like:


Some difficulty has arisen with the Pyramids, since their set of moves is determined by which pieces belong to them at the moment. It was necessary to describe all possible moves for them, and when making a move, check the presence in the set of the corresponding figure:


The implementation of the battle of figures turned into a real "race for survival." It was necessary to implement four completely different (and very nontrivial) ways of taking. At the same time, I wanted to limit the number of field views in order to minimize the overhead of calculations (the course is already calculated ugly for a long time). As a result, I settled on the idea of ​​pre-filling several arrays, with the implementation of subsequent checks on the conditions of the battle of figures:


The capture of figures in the Pyramid, as well as the displacement, had to be processed in a special way:


Already in the process of debugging, I realized that all the checks are performed at the time before the progress. I had to write a small function imitating the movement of the figure (this is not a complete recalculation of the position on the board, but I managed to get by with a little blood):


Against the background of all these horrors, checking the conditions for completing the game seemed like a trivial task. There was a small amount of Axiom magic, but there is nothing here that I would be afraid to show my parents:


From this point on, the program could already play (although it did it rather passively). The fact is that, in the absence of an evaluation function (and the custom implementation of AI), Axiom tries to perform a complete search, to a terminal position. It is clear that the completion of the game is far beyond the horizon of the possible depth of enumeration, as a result of which, the found moves are not particularly meaningful. In general, it remains to add AI teeth:


Here, a very convenient material-balance function (provided by Axiom) is used, which uses the weight values ​​specified for the figures (the same values ​​are used for the implementation of the Rhythmochial rules):


This implementation lacks a lot (for example, checking the end of the game for Glorious Victories ). I will try to add the missing functionality in the future. The current version of the source can always be found here .

What is the result?

Ritmomachia interested me, first of all, in its complexity. Of course, there were no thoughts to implement it on ZRF . I had to master Axiom , for this! Currently, there is a simplified implementation that does not support Glorious Victories . Also, there is no firm certainty that I found all the errors in the code (1000 lines in ForthScript is serious). This is a beta version, but in general, it works:



You may notice that the game ends very quickly. It really is. In case both players play aggressively, under the conditions of Common Victories (and without limiting the number of pieces taken), the average duration of the game is ~ 10 moves. In this case, the first player has a significant advantage:

 Cumulative results following game 13 of 100: Player 1 "Eval", wins = 13. Player 2 "Eval", wins = 0. Draws = 0 

It's funny that if only one of the players is aggressive, the game is delayed to more than 300 moves (the aggressive player almost always wins).

 Cumulative results following game 22 of 100: Player 1 "Rithmomachy", wins = 1. Player 2 "Eval", wins = 21. Draws = 0 

It's hard to play with a computer. Even with the illumination of the figures that are under combat, it is not easy to figure out which particular figure should make a move in order to accomplish the capture (at the same time, it is desirable not to substitute your own figures). In our time, this game is unlikely to be popular, but one does not take away from her. She is great at developing oral skill.