Factorization and classes of natural numbers
We accept abbreviations: natural number series (NPS); the problem of factoring large numbers (ZFBCH).
Manipulation with natural numbers is possible both directly with values, and with characteristics - properties of numbers. The convenience of such manipulation is largely determined by the number model. It is desirable to have a variety of models limited, and the structural structure is simple. Descriptions of the properties of models of natural numbers (by the way, any other numbers) are desirable to have in quantitative terms, in a formalized form. The dependence of property values of indicators on the digit capacity of numbers must be eliminated, or properties free from such dependencies should be chosen. Any classification basically has properties - it is an element of formalization. The main question in the paper is factorization of numbers. In connection with this, we will formulate a variant of the factorization theorem of a natural number below.
The theorem says that difficulties of factorization do not arise for all numbers, therefore, the complex procedure of factorization does not need to expose not all the numbers of the NPS, but only some (smaller) part of them. The text of the theorem does not say how to formalize this smaller part and make it convenient for further processing. But in the paper, it will be just a matter of forming a presentation of numbers of such a smaller set that is convenient for processing.
Theorem of factorization of natural numbers
An arbitrary composite positive integer N by successively performing some elementary transformations on it can be represented as a product of the form
N = 2 t 2 ∙ 3 t 3 ∙ 5 t 5 ∙ (p k + 30 ∙ t), where 0 ≤ t i , i = 2,3,5, t is natural, k > 5 is simple.
Theorem
1. If N is a composite even positive integer, then it can be represented as N = 2 t 2 ∙ n 2 ,
where n 2 1 (mod 2) is a composite odd number, t 2 = 1 (1) ..., and 2 ∤ n 2 ;
2. If N = n 2 is a compound odd number ending in 5, then it can be represented as N = 5 t 5 ∙ n 5 , where n 5 is a compound odd number, t 5 = 1 (1) ...; and 5 ∤ n 5 ;
3. If N = n 5 is a compound odd number that does not end with 5, and its convolution s (N) (sum of digits) is a multiple of 3, then it can be represented as N = 3 t 3 n 3 , where n 3 - compound odd number
t 3 = 1 (1) ...; and 3 ∤ n 3 ;
4. If N = n 3 is a composite odd number, with the last digit, {1, 3, 7, 9}, then it has the form N = (p k + 30 ∙ t), where t = 1 ( 1) ... is a natural number, and p k ϵ {7,11,13,17,19,23,29,31}, and factorization can be performed, for example, using the notion of limit contour and Φ-invariant of an odd number or one of the existing known methods.
')
Instead of proof. Further, the text of the work, including Table 3, is essentially the proof of the first part of the theorem (on the representation of a number as a model N = 30 ∙ t + p k ). In the course of the presentation, complete and truncated NPS models, flat and three-dimensional, appear. The set of all natural numbers is divided into two subsets. The first is that the intuitively perceived as more contains natural numbers that are factored by elementary means (the simplest signs of divisibility into prime numbers 2, 3, 5 are used). The second subset is the smallest, which contains all the odd simple ones (except 3 and 5), and the factorization of which is especially for large numbers an insurmountable problem of the present. The last factorial number known from publications is described by 232 decimal digits.
The well-known analytical model of NPS in the form of a list 30k, 30k ± 1, 30k ± 3, ..., 30k ± 15,
k = 1 (1) ∞, relations allows us to understand how to describe those of the numbers that should be contained in each of these subsets, that is, in essence, to perform such a partition of the NPS.
The multiplicative representation of the number 30 has the form 30 = 2 ∙ 3 5. Natural numbers N, comparable to zero modulo divisors of 30,N ≡ 0 (mod2), N ≡ 0 (mod3), N ≡ 0 (mod5) are all even numbers, numbers divisible by three without a remainder, and odd numbers ending in 5.
It turns out that the set of natural numbers with violation of similar properties splits into equivalence classes with other simple, well distinguishable signs. Thus, the task in the work consists in dividing the NSP into two subsets, and obtaining a smaller description in a simple and convenient form for further processing of numbers.
Classes of natural numbers. Let us base the classification under consideration on two very simply defined indicators of the properties (s, φ) of numbers. The first indicator is denoted by s,
1 ≤ s ≤ 9, is called convolution (this is the sum of digits of a number, brought up to one digit) of a number, it characterizes the divisibility property of a number by three, and the second indicator is denoted by the symbol ,
0 ≤ f ≤ 9, - called the flexion (ending, last digit) of a number, characterizes the property of a finite number to have the last digit.
Example 1 N = 4757, s (N) = ((4 + 7 + 5 + 7 = 23) → (2 + 3)) = 5; f (N) ≡ N (mod10) = 7.
A pair of properties of numbers characterized by indicators (s, φ) breaks the NPS into non-intersecting classes (equivalences) that have the same values of a pair of indicators. A characteristic of the class of numbers to which the number N = 4757 belongs is a pair with the value (s, φ) = (5, 7).
The number T (s, f) of classes of numbers distinguishable by such a characteristic is determined by the product of the ranges of changes in the values of each indicator of the two properties of the number
T (S, F) = S × F = 9 × 10 = 90.
The volume of each class includes an infinite number of natural numbers, among which is the smallest number in the class. Place the smallest representatives of all classes in the left part of Table 1, and continue it to the right, filling (on the model to the left) the cells of the tables in a row with the following natural numbers.
Table 1 - Classes T (s, f) of numbers with a period of 90. Plane model NPS

An analysis of the contents of the table (a set of T-90 numbers) shows that on the left side of the 10 × 9 table, all numbers are the smallest in their class and have different characteristic values (s, φ). The right side of the 10 × 9 table, similarly to the left, is filled with representatives of different classes with the same characteristic (s, f), but with the next element (period) increased by 90 units. Such tables can be continued to infinity and shifted to the left with overlapping on the 1st (left) table. As a result, we obtain a three-dimensional parallelepiped, in which over each cell of the lower table we write out all the numbers that form the class of natural numbers with a fixed value of the pair (s, φ).
Volumetric model NPS
In essence, we have obtained one more already bulk model of NPS. Its advantages are manifested in the ability to significantly reduce the NPS without losing important positions, for example, positions containing prime numbers. We show how this can be done.
First, we cross out the rows of table 1 containing even numbers and odd numbers ending in a five, and second, delete classes of numbers that are multiples of a three. The cells of the table of such classes belong to the diagonals parallel to the secondary diagonal of the table. In Table 1, deleted cells (classes) are highlighted with a fill.
Not painted over cells-classes T (s, φ) have remained, the number of which is 24 (we will call the numbers remaining after crossing out the set T-24), they correspond to the table cells without a fill. Possible inflections in the remaining classes are only φ = 1,3,7,9 and with each flexion there are 6 convolution values each, that is, 24 classes. It is quite obvious that prime numbers can appear within only these classes. Indeed, in the left table of the 24 smallest representatives of all classes, 22 are prime numbers. Only two cells (out of 24) are filled with the composite numbers 7 × 7 = 49 and7 × 11 = 77 , obtained by multiplying the smallest remaining prime number 7 by itself and by the next prime number 11.
Algebraic group residue class generators
We will continue the reform of the NPS, back to the number 30 = 2 ∙ 3 5. Recall that the eight prime numbers p (i) = {7,11,13,17,19,23,29,31} forms a multiplicative group E (Euler group) of eighth-order residues along this module. A single element is identified with the prime number 31, p (i) ≡ 31 (mod30) = 1. By the Lagrange theorem (on orders of groups), the group E can have its own subgroups of the 2nd and 4th orders. The elements of the 8th order group (11,19 and 29) are of the 2nd order; (7.13, 17, 23) 4th order and unit. There are three subgroups of the fourth order: one (1,11,19,29) - it includes only involutions, and two cyclic subgroups:
7 × 7 ≡ 49 (mod30) = 19; 19 × 7 ≡ 133 (mod30) = 13; 13 × 7 ≡ 91 (mod30) = 1;
11 × 19 209 (mod30) = 29; 11 × 29 ≡ 319 (mod30) = 19; 19 × 29 ≡ 551 (mod30) = 1;
17 × 17 ≡ 289 (mod30) = 19; 19 × 17 ≡ 323 (mod30) = 23; 23 × 17≡ 391 (mod30) = 1;
Surprisingly, but all numbers are 24 classes | T (S, F) | = 3 × 8 are transformed into a class family consisting of only 8 classes generated by each representative of the set p (i). In the new classes, the numbers - elements follow with a period no longer 90, but three times smaller, only 30.
Table 2 - Multiplicative subgroups of the residue group (p k ) mod30
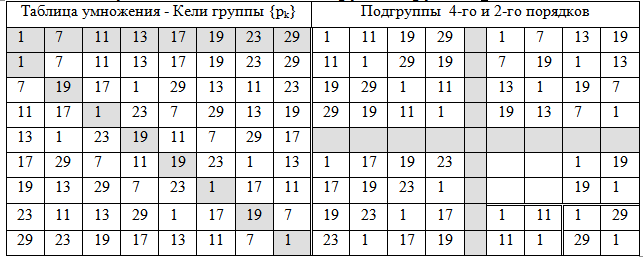
Classes are formed taking into account the flexion and convolution of numbers of three pairs (2,1), (5,1), (8,1); (4,1), (7,1), (1,1); (2.3), (5.3), (8.3); (4.3), (7.3), (1.3); (7.7), (1.7), (4.7); (8.7), (2.7), (5.7); (7.9), (1.9), (4.9); (8.9), (2.9), (5.9);
Below in Table 3 we give the initial fragments of these 8 classes. Any odd number N> 31 not a multiple of 3 or 5 has the form N = p (i) + 30t and falls into one of the 8 classes presented in Table 3. We call the set of numbers from such a table the set T - 8.
Table 3 - Classes of numbers with a period of 30. Prime numbers {p k } are highlighted with a fill.

Even a superficial analysis of the table allows us to draw some conclusions regarding simplicity, complexity, and the possibility of factoring numbers:
- all degrees of all class generators, i.e. prime numbers - composite;
- the lines with the number multiple to the generator in the cell of the column of this generator contain composite numbers, the divisor of which is the generator;
- numbers belonging to the area of prohibition of primes in the Ulam spiral, - composite, examples of such numbers in the first thousand: 143,161,203,217,323,451, 517,539,473, 611,637, etc.
- numbers that allow decomposition into a sum-difference and putting out a common factor, for example, 217 = 210 + 7 = 7 (30 +1) = 7 × 31; 1397 = 1270 + 127 = 127 (10 + 1) = 127 × 11.
Thus, by elementary means and operations, it is possible to select a set of T-8 odd numbers of NPS, which should and can serve as the object of subsequent research in the interest of solving both theoretical and applied practical problems. Such tasks in the field of cryptology and information security include the following: ZFSB, the problem of establishing the simplicity of a number, the problem of a discrete logarithm in finite fields and groups of points of elliptic curves.
The set of numbers T-8 is organized in a special way (consists of 8 classes), the smallest representatives of the classes form a group of residues modulo 30 (φ (30) = 8). This property provides the definition of the column number of the result of the product of a pair of numbers whose column numbers are known. Table Keli group provides a solution to this problem.
The purpose of the examples is to show what information about the connections of the values of numbers, row numbers and column numbers is contained in the set T-8.
One of the possible methods of factoring the numbers of the T-8 set using Table 3.
Example 2 Let a composite odd natural number be given (snnch)
N = 1727. Factoring is required. Find the position of this number in the set T-8: the row number is N / 30 = 57 (the integer part of the fraction is taken), the number (name) of the column N is 30 17. 57 = 17. In the same column we specify the product 7 ∙ 11 = 77, the number which line is 2.
We try to save each of the dividers. Save d1 = 7, another divider N takes the form
d2 = 11 + 30 ∙ t, where t is determined by the difference of line numbers and the divisor is saved
t = (57 - 2) / 7 = 7.85. We got a fractional value, which means that 7 is not a divisor of a given number of 1727. In fact, you can immediately try to find out if di is a divisor of a given number.
Save d2 = 11, another divider takes the form d1 = 7 + 30 30 t, where t is determined through the difference of line numbers and the stored divisor t = (57 - 2) / 11 = 5. Then d1 = 7 + 30 ∙ t = 157.
Indeed, 1727/157 = 11.
Example 3. Let the compound odd positive integer (snnch) be set
N = 4294967297, outside the table. It is required to factor it. Find, as before, the position of this number in the T-8 set:
line number N / 30 = 143165576,
column number N - 30 ∙ 143165576 = 17.
In the same column, we specify the product 7 ∙ 641 = 4487, the row number of which is 149.
We try to save each of the dividers. Save d1 = 641, another divider takes the form
7 + 30 ∙ t, where t is determined by the difference of lines and the saved divisor
t = (143165576 - 149) / 641 = 143165427/641 = 223347.
The value t = 223347 is an integer, therefore, 641 is a divisor of the original number N.
Indeed, N / d1 = 4294967297: 641 = 6700417 is a prime number (another divisor).
Manipulation with natural numbers is possible both directly with values, and with characteristics - properties of numbers. The convenience of such manipulation is largely determined by the number model. It is desirable to have a variety of models limited, and the structural structure is simple. Descriptions of the properties of models of natural numbers (by the way, any other numbers) are desirable to have in quantitative terms, in a formalized form. The dependence of property values of indicators on the digit capacity of numbers must be eliminated, or properties free from such dependencies should be chosen. Any classification basically has properties - it is an element of formalization. The main question in the paper is factorization of numbers. In connection with this, we will formulate a variant of the factorization theorem of a natural number below.
The theorem says that difficulties of factorization do not arise for all numbers, therefore, the complex procedure of factorization does not need to expose not all the numbers of the NPS, but only some (smaller) part of them. The text of the theorem does not say how to formalize this smaller part and make it convenient for further processing. But in the paper, it will be just a matter of forming a presentation of numbers of such a smaller set that is convenient for processing.
Theorem of factorization of natural numbers
An arbitrary composite positive integer N by successively performing some elementary transformations on it can be represented as a product of the form
N = 2 t 2 ∙ 3 t 3 ∙ 5 t 5 ∙ (p k + 30 ∙ t), where 0 ≤ t i , i = 2,3,5, t is natural, k > 5 is simple.
Theorem
1. If N is a composite even positive integer, then it can be represented as N = 2 t 2 ∙ n 2 ,
where n 2 1 (mod 2) is a composite odd number, t 2 = 1 (1) ..., and 2 ∤ n 2 ;
2. If N = n 2 is a compound odd number ending in 5, then it can be represented as N = 5 t 5 ∙ n 5 , where n 5 is a compound odd number, t 5 = 1 (1) ...; and 5 ∤ n 5 ;
3. If N = n 5 is a compound odd number that does not end with 5, and its convolution s (N) (sum of digits) is a multiple of 3, then it can be represented as N = 3 t 3 n 3 , where n 3 - compound odd number
t 3 = 1 (1) ...; and 3 ∤ n 3 ;
4. If N = n 3 is a composite odd number, with the last digit, {1, 3, 7, 9}, then it has the form N = (p k + 30 ∙ t), where t = 1 ( 1) ... is a natural number, and p k ϵ {7,11,13,17,19,23,29,31}, and factorization can be performed, for example, using the notion of limit contour and Φ-invariant of an odd number or one of the existing known methods.
')
Instead of proof. Further, the text of the work, including Table 3, is essentially the proof of the first part of the theorem (on the representation of a number as a model N = 30 ∙ t + p k ). In the course of the presentation, complete and truncated NPS models, flat and three-dimensional, appear. The set of all natural numbers is divided into two subsets. The first is that the intuitively perceived as more contains natural numbers that are factored by elementary means (the simplest signs of divisibility into prime numbers 2, 3, 5 are used). The second subset is the smallest, which contains all the odd simple ones (except 3 and 5), and the factorization of which is especially for large numbers an insurmountable problem of the present. The last factorial number known from publications is described by 232 decimal digits.
The well-known analytical model of NPS in the form of a list 30k, 30k ± 1, 30k ± 3, ..., 30k ± 15,
k = 1 (1) ∞, relations allows us to understand how to describe those of the numbers that should be contained in each of these subsets, that is, in essence, to perform such a partition of the NPS.
The multiplicative representation of the number 30 has the form 30 = 2 ∙ 3 5. Natural numbers N, comparable to zero modulo divisors of 30,
It turns out that the set of natural numbers with violation of similar properties splits into equivalence classes with other simple, well distinguishable signs. Thus, the task in the work consists in dividing the NSP into two subsets, and obtaining a smaller description in a simple and convenient form for further processing of numbers.
Classes of natural numbers. Let us base the classification under consideration on two very simply defined indicators of the properties (s, φ) of numbers. The first indicator is denoted by s,
1 ≤ s ≤ 9, is called convolution (this is the sum of digits of a number, brought up to one digit) of a number, it characterizes the divisibility property of a number by three, and the second indicator is denoted by the symbol ,
0 ≤ f ≤ 9, - called the flexion (ending, last digit) of a number, characterizes the property of a finite number to have the last digit.
Example 1 N = 4757, s (N) = ((4 + 7 + 5 + 7 = 23) → (2 + 3)) = 5; f (N) ≡ N (mod10) = 7.
A pair of properties of numbers characterized by indicators (s, φ) breaks the NPS into non-intersecting classes (equivalences) that have the same values of a pair of indicators. A characteristic of the class of numbers to which the number N = 4757 belongs is a pair with the value (s, φ) = (5, 7).
The number T (s, f) of classes of numbers distinguishable by such a characteristic is determined by the product of the ranges of changes in the values of each indicator of the two properties of the number
T (S, F) = S × F = 9 × 10 = 90.
The volume of each class includes an infinite number of natural numbers, among which is the smallest number in the class. Place the smallest representatives of all classes in the left part of Table 1, and continue it to the right, filling (on the model to the left) the cells of the tables in a row with the following natural numbers.
Table 1 - Classes T (s, f) of numbers with a period of 90. Plane model NPS

An analysis of the contents of the table (a set of T-90 numbers) shows that on the left side of the 10 × 9 table, all numbers are the smallest in their class and have different characteristic values (s, φ). The right side of the 10 × 9 table, similarly to the left, is filled with representatives of different classes with the same characteristic (s, f), but with the next element (period) increased by 90 units. Such tables can be continued to infinity and shifted to the left with overlapping on the 1st (left) table. As a result, we obtain a three-dimensional parallelepiped, in which over each cell of the lower table we write out all the numbers that form the class of natural numbers with a fixed value of the pair (s, φ).
Volumetric model NPS
In essence, we have obtained one more already bulk model of NPS. Its advantages are manifested in the ability to significantly reduce the NPS without losing important positions, for example, positions containing prime numbers. We show how this can be done.
First, we cross out the rows of table 1 containing even numbers and odd numbers ending in a five, and second, delete classes of numbers that are multiples of a three. The cells of the table of such classes belong to the diagonals parallel to the secondary diagonal of the table. In Table 1, deleted cells (classes) are highlighted with a fill.
Not painted over cells-classes T (s, φ) have remained, the number of which is 24 (we will call the numbers remaining after crossing out the set T-24), they correspond to the table cells without a fill. Possible inflections in the remaining classes are only φ = 1,3,7,9 and with each flexion there are 6 convolution values each, that is, 24 classes. It is quite obvious that prime numbers can appear within only these classes. Indeed, in the left table of the 24 smallest representatives of all classes, 22 are prime numbers. Only two cells (out of 24) are filled with the composite numbers 7 × 7 = 49 and
Algebraic group residue class generators
We will continue the reform of the NPS, back to the number 30 = 2 ∙ 3 5. Recall that the eight prime numbers p (i) = {7,11,13,17,19,23,29,31} forms a multiplicative group E (Euler group) of eighth-order residues along this module. A single element is identified with the prime number 31, p (i) ≡ 31 (mod30) = 1. By the Lagrange theorem (on orders of groups), the group E can have its own subgroups of the 2nd and 4th orders. The elements of the 8th order group (11,19 and 29) are of the 2nd order; (7.13, 17, 23) 4th order and unit. There are three subgroups of the fourth order: one (1,11,19,29) - it includes only involutions, and two cyclic subgroups:
7 × 7 ≡ 49 (mod30) = 19; 19 × 7 ≡ 133 (mod30) = 13; 13 × 7 ≡ 91 (mod30) = 1;
11 × 19 209 (mod30) = 29; 11 × 29 ≡ 319 (mod30) = 19; 19 × 29 ≡ 551 (mod30) = 1;
17 × 17 ≡ 289 (mod30) = 19; 19 × 17 ≡ 323 (mod30) = 23; 23 × 17≡ 391 (mod30) = 1;
Surprisingly, but all numbers are 24 classes | T (S, F) | = 3 × 8 are transformed into a class family consisting of only 8 classes generated by each representative of the set p (i). In the new classes, the numbers - elements follow with a period no longer 90, but three times smaller, only 30.
Table 2 - Multiplicative subgroups of the residue group (p k ) mod30

Classes are formed taking into account the flexion and convolution of numbers of three pairs (2,1), (5,1), (8,1); (4,1), (7,1), (1,1); (2.3), (5.3), (8.3); (4.3), (7.3), (1.3); (7.7), (1.7), (4.7); (8.7), (2.7), (5.7); (7.9), (1.9), (4.9); (8.9), (2.9), (5.9);
Below in Table 3 we give the initial fragments of these 8 classes. Any odd number N> 31 not a multiple of 3 or 5 has the form N = p (i) + 30t and falls into one of the 8 classes presented in Table 3. We call the set of numbers from such a table the set T - 8.
Table 3 - Classes of numbers with a period of 30. Prime numbers {p k } are highlighted with a fill.

Even a superficial analysis of the table allows us to draw some conclusions regarding simplicity, complexity, and the possibility of factoring numbers:
- all degrees of all class generators, i.e. prime numbers - composite;
- the lines with the number multiple to the generator in the cell of the column of this generator contain composite numbers, the divisor of which is the generator;
- numbers belonging to the area of prohibition of primes in the Ulam spiral, - composite, examples of such numbers in the first thousand: 143,161,203,217,323,451, 517,539,473, 611,637, etc.
- numbers that allow decomposition into a sum-difference and putting out a common factor, for example, 217 = 210 + 7 = 7 (30 +1) = 7 × 31; 1397 = 1270 + 127 = 127 (10 + 1) = 127 × 11.
Thus, by elementary means and operations, it is possible to select a set of T-8 odd numbers of NPS, which should and can serve as the object of subsequent research in the interest of solving both theoretical and applied practical problems. Such tasks in the field of cryptology and information security include the following: ZFSB, the problem of establishing the simplicity of a number, the problem of a discrete logarithm in finite fields and groups of points of elliptic curves.
The set of numbers T-8 is organized in a special way (consists of 8 classes), the smallest representatives of the classes form a group of residues modulo 30 (φ (30) = 8). This property provides the definition of the column number of the result of the product of a pair of numbers whose column numbers are known. Table Keli group provides a solution to this problem.
The purpose of the examples is to show what information about the connections of the values of numbers, row numbers and column numbers is contained in the set T-8.
One of the possible methods of factoring the numbers of the T-8 set using Table 3.
Example 2 Let a composite odd natural number be given (snnch)
N = 1727. Factoring is required. Find the position of this number in the set T-8: the row number is N / 30 = 57 (the integer part of the fraction is taken), the number (name) of the column N is 30 17. 57 = 17. In the same column we specify the product 7 ∙ 11 = 77, the number which line is 2.
We try to save each of the dividers. Save d1 = 7, another divider N takes the form
d2 = 11 + 30 ∙ t, where t is determined by the difference of line numbers and the divisor is saved
t = (57 - 2) / 7 = 7.85. We got a fractional value, which means that 7 is not a divisor of a given number of 1727. In fact, you can immediately try to find out if di is a divisor of a given number.
Save d2 = 11, another divider takes the form d1 = 7 + 30 30 t, where t is determined through the difference of line numbers and the stored divisor t = (57 - 2) / 11 = 5. Then d1 = 7 + 30 ∙ t = 157.
Indeed, 1727/157 = 11.
Example 3. Let the compound odd positive integer (snnch) be set
N = 4294967297, outside the table. It is required to factor it. Find, as before, the position of this number in the T-8 set:
line number N / 30 = 143165576,
column number N - 30 ∙ 143165576 = 17.
In the same column, we specify the product 7 ∙ 641 = 4487, the row number of which is 149.
We try to save each of the dividers. Save d1 = 641, another divider takes the form
7 + 30 ∙ t, where t is determined by the difference of lines and the saved divisor
t = (143165576 - 149) / 641 = 143165427/641 = 223347.
The value t = 223347 is an integer, therefore, 641 is a divisor of the original number N.
Indeed, N / d1 = 4294967297: 641 = 6700417 is a prime number (another divisor).
Source: https://habr.com/ru/post/234277/
All Articles