Linear cryptanalysis for dummies

Hi% username%!
Many people know that the DES algorithm has long been considered the default standard in the field of symmetric encryption. The first successful attack on this unkillable algorithm was published in 1993, 16 years after its adoption as a standard. The method, which the author called linear cryptanalysis, in the presence of 2 ⁴⁷ pairs of open / encrypted texts, allows you to unlock the secret DES cipher key for 2 ⁴³ operations.
Under the cut, I will try to briefly outline the main points of this attack.

Linear cryptanalysis

Linear cryptanalysis is a special kind of attack on symmetric ciphers, aimed at recovering an unknown encryption key, using known open messages and corresponding ciphertexts.

In the general case, an attack based on linear cryptanalysis is reduced to the following conditions. The attacker has a large number of pairs of open / encrypted text obtained using the same encryption key K. The attacker's goal is to restore part or all of the K key.

First of all, the attacker makes a study of the cipher and finds a so-called. statistical counterpart, i.e. The equation of the following form, which is executed with probability P ≠ 1/2 for an arbitrary pair of open / closed text and a fixed key:
P _I1 ⊕ P _I2 ⊕ ... ⊕ P _Ia ⊕ C _I1 ⊕ C _I2 ⊕ ... C _Ib = K _I1 ⊕ K _I2 ⊕ ... ⊕ K _Ic (1) ,
where P _n , C _n , K _n are the n-th bits of the text, ciphertext and key.
After a similar equation is found, the attacker can recover 1 bit of key information using the following algorithm.
')
Algorithm 1
Let T be the number of texts for which the left side of equation (1) is 0, then
If T> N / 2, where N is the number of known open texts.
Suppose that K _I1 ⊕ K _I2 ⊕ ... ⊕ K _Ic = 0 (when P> 1/2) or 1 (when P <1/2).
Otherwise
Suppose that K _I1 ⊕ K _I2 ⊕ ... ⊕ K _Ic = 1 (when P> 1/2) or 0 (when P <1/2).
It is obvious that the success of the algorithm directly depends on the value of | P-1/2 | and the number of open / closed text pairs available N. The greater the probability P of equality (1) differs from 1/2, the smaller the number of clear texts N is necessary for an attack.

There are two problems that must be solved for the successful implementation of the attack:

• How to find an effective equation of the form (1).
• How to get more than one bit of key information using such an equation.

Consider the solution of these issues on the example of the cipher DES.

DES description

But first, let's briefly describe the operation of the algorithm. About DES said enough. A full description of the cipher can be found on Wikipedia . However, to further explain the attack, we will need a number of definitions which are better to enter in advance.

So, DES is a block cipher based on a Feistel network . The cipher has a block size of 64 bits and a key size of 56 bits. Consider the DES encryption scheme.

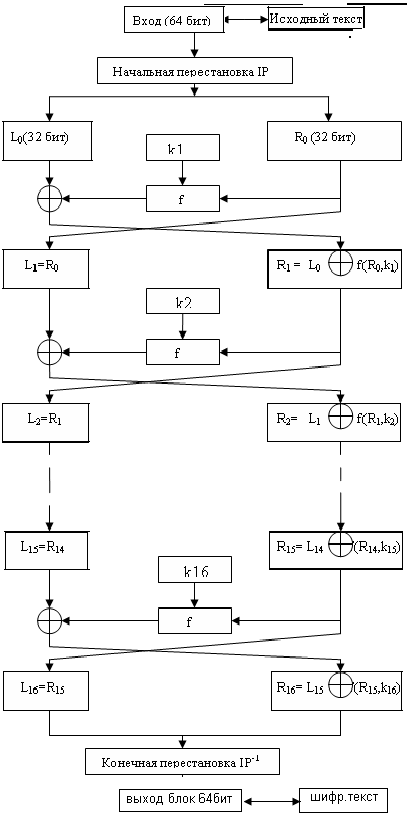
As can be seen from the figure, the following operations are performed when encrypting the text:

1. The initial permutation bits. At this stage, the bits of the input block are mixed in a certain order.
2. After that, the mixed bits are divided into two halves, which are fed to the input of the Feistel function. For standard DES, the Feistel network includes 16 rounds, but there are other variants of the algorithm.
3. The two blocks obtained in the last round of the transformation are combined and one more permutation is performed on the obtained block.

At each round of the Feistel network, the 32 low bits of the message go through function f:

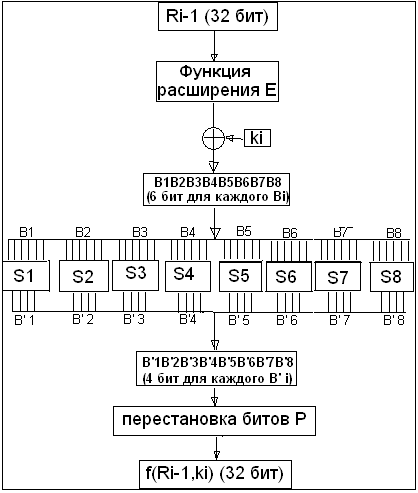
Consider the operations that are performed at this stage:

1. The input block passes through the extension function E, which converts a 32-bit block into a block with a length of 48 bits.
2. The resulting block is formed with a round key K _i .
3. The result of the previous step is divided into 8 blocks of 6 bits each.
4. Each of the received B _i blocks passes through the S-Box _i substitution function, which replaces the 6-bit sequence, with a 4-bit block.
5. The resulting 32-bit block passes through the permutation P and is returned as the result of the function f.

From the point of view of cryptanalysis of the cipher, S blocks are of the greatest interest to us, which are designed to hide the connection between the input and output data of the function f. For a successful attack on DES, we first build statistical counterparts for each of the S-boxes, and then extend them to the entire cipher.

S block analysis

Each S-block accepts a 6-bit sequence at the input, and for each such sequence a fixed 4-bit value is returned. Those. There are a total of 64 input and output options. Our task is to show the relationship between input and output data of S blocks. For example, for the third S-block of the DES cipher, the 3rd bit of the input sequence is equal to the 3rd bit of the output sequence in 38 cases out of 64. Therefore, we found the following statistical equivalent for the third S-block:
S ₃ (x) [3] = x [3], which is performed with the probability P = 38/64.
Both sides of the equation represent 1 bit of information. Therefore, if the left and right sides were independent of each other, the equation would have to be performed with a probability equal to 1/2. Thus, we have just demonstrated the relationship between the input and output data of the 3rd S-block of the DES algorithm.

Consider how you can find the statistical analogue of the S-block in the general case.

For the S-box, S _a , 1 ≤ α ≤ 63 and 1 ≤ β ≤ 15, the NS value of _a (α, β) describes how many times out of 64 possible XOR input bits S _a superimposed on bits α are equal to the XOR output bits superimposed on the bits β, i.e .:
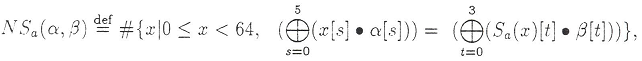where the symbol • - logical I.
The values ​​of α and β, for which NS _a (α, β) is most different from 32, describe the most effective statistical analogue of the S-block S _a .

The most effective analog was found in the 5th S-block of the DES cipher for α = 16 and β = 15 NS ₅ (16, 15) = 12. This means that the following equation holds: Z [2] = Y [1] ⊕ Y [2] ⊕ Y [3] ⊕ Y [4], where Z is the input sequence of the S-box and Y is the output sequence.
Or taking into account the fact that in the DES algorithm, before entering the S-block, the data is added modulo 2 with a round key, i.e. Z [2] = X [2] ⊕ K [2] we get
X [2] ⊕ Y [1] ⊕ Y [2] ⊕ Y [3] ⊕ Y [4] = K [2], where X and Y are the input and output data of the function f without considering the permutations.
The resulting equation is performed on all rounds of the DES algorithm with the same probability P = 12/64.
The following table lists the effective ones, i.e. having the greatest deviation from P = 1/2, statistical analogues for each s-block of the DES algorithm.

Construction of statistical analogues for several rounds of DES

We now show how to combine statistical analogues of several DES rounds and eventually get a statistical analog for the entire cipher.
To do this, consider the three-round version of the algorithm:

Let us apply the effective statistical analogue of the 5th s-block to calculate certain bits of the X (2) value.
We know that with the probability of 12/64 in the f-function, the equality X [2] ⊕ Y [1] ⊕ Y [2] ⊕ Y [3] ⊕ Y [4] = K [2] holds , where X [2] is the second input bit of the 5th S-box, it is essentially the 26th bit of the sequence obtained after expanding the input bits. Analyzing the expansion function, it can be established that in place of 26 bits is the 17th bit of the X (1) sequence.
Similarly, Y [1], ..., Y [4] are essentially the 17th, 18th, 19th and 20th bit of the sequence obtained before the permutation P. Examining the permutation P, we get that the bits Y [1] , ..., Y [4] are actually bits of Y (1) [3], Y (1) [8], Y (1) [14], Y (1) [25].
The key bit K [2] involved in the equations is the 26th subkey key of the first round K1 and then the statistical analogue takes the following form:
X (1) [17] ⊕ Y (1) [3] ⊕ Y (1) [8] ⊕ Y1 [14] ⊕ Y (1) [25] = K1 [26] .
Therefore, X (1) [17] ⊕ K1 [26] = Y (1) [3] ⊕ Y (1) [8] ⊕ Y (1) [14] ⊕ Y (1) [25] (2) with probability P = 12/64.
Knowing the 3, 8, 14, 25 bits of the sequence Y (1) you can find 3, 8, 14, 25 bits of the sequence X (2):
X (2) [3] ⊕ X (2) [8] ⊕ X (2) [14] X (2) [25] = PL [3] ⊕ PL [8] PL [14] PL [25 ] ⊕ Y (1) [3] ⊕ Y (1) [8] ⊕ Y (1) [14] ⊕ Y (1) [25] or taking into account equation (2)
X (2) [3] ⊕ X (2) [8] ⊕ X (2) [14] X (2) [25] = PL [3] ⊕ PL [8] PL [14] PL [25 ] ⊕ X (1) [17] ⊕ K1 [26] (3) with a probability of 12/64.

We will find a similar expression using the last round. This time we have the equation
X (3) [17] ⊕ K3 [26] = Y (3) [3] ⊕ Y (3) [8] ⊕ Y (3) [14] ⊕ Y (3) [25] .
Because
X (2) [3] ⊕ X (2) [8] ⊕ X (2) [14] ⊕ X (2) [25] = CL [3] ⊕ CL [8] CL [14] ⊕ CL [25 ] ⊕ Y (3) [3] ⊕ Y (3) [8] ⊕ Y (3) [14] ⊕ Y (3) [25]
we get that
X (2) [3] ⊕ X (2) [8] ⊕ X (2) [14] ⊕ X (2) [25] = CL [3] ⊕ CL [8] CL [14] ⊕ CL [25 ] ⊕ X (3) [17] ⊕ K3 [26] (4) with a probability of 12/64.

Equating the right sides of equations (3) and (4) we obtain
L [3] ⊕ L [8] ⊕ L [14] ⊕ L [25] ⊕ X (3) [17] ⊕ K3 [26] = PL [3] PL [8] PL [14] PL [ 25] ⊕ X (1) [17] ⊕ K1 [26] with probability (12/64) ² + (1-12 / 64) ² .
Taking into account that X (1) = PR and X (3) = CR, we obtain a statistical analogue
L [3, 8, 14, 25] ⊕ CR [17] ⊕ PL [3, 8, 14, 25] ⊕ PR [17] = K1 [26] ⊕ K3 [26] (5) ,
which is performed with the probability (12/64) ² + (1-12 / 64) ² = 0.7.
The statistical analogue described above can be represented graphically as follows (the bits in the figure are numbered from right to left and starting from zero):

All bits on the left side of the equation are known to the attacker, therefore he can apply algorithm 1 and find out the value of K1 [17] ⊕ K3 [17]. Let us show how using this statistical analogue, you can open not 1, but 12 bits of the encryption key K.

Known plain text attack on DES

We give a way with which you can expand the attack and get immediately 6 bits of the subkey of the first round.
When composing equation (5), we took into account the fact that we do not know the value of F1 (PR, K1) [3, 8, 14, 25]. Therefore, we used its statistical analogue K1 [26] ⊕ PR [17].
Instead of the expression K1 [26] ⊕ PR [17], we return the value F1 (PR, K1) [3, 8, 14, 25] and we get the following equation:
L [3, 8, 14, 25] ⊕ CR [17] ⊕ PL [3, 8, 14, 25] ⊕ F1 (PR, K1) [3, 8, 14, 25] = K3 [26] (6) which will be executed with a probability of 12/64. The probability has changed since we left only the statistical counterpart from the third round, all other values ​​are fixed.

Above, we have already determined that the value of F1 (PR, K1) [3, 8, 14, 25] is influenced by the input bits of the 5th S-block, namely the key bits K1 [25 ~ 30] and the bits of the PR block [16 ~ 21]. We show how having only a set of open / closed texts, you can restore the value of K1 [25 ~ 30]. To do this, we use algorithm 2.

Algorithm 2
Let N be the number of open / closed text pairs known before the attack. Then to open the key, you must do the following steps.
For (i = 0; i <64; i ++) do
{
For (j = 0; j <N; j ++) do
{
if (L _j [3, 8, 14, 25] ⊕ CR _j [17] ⊕ PL _j [3, 8, 14, 25] ⊕ F1 (PR _j , i) [3, 8, 14, 25] = 0 ) then
T _i = T _i +1
}
}
As a probable sequence K1 [25 ~ 30], the value of i is taken such that the expression | T _i -N / 2 | has a maximum value.

With a sufficient number of known open texts, the algorithm will most likely return the correct value of six bits of the subkey of the first round K1 [25 ~ 30]. This is explained by the fact that if the variable i is not equal to K1 [25 ~ 30], then the value of the function F1 (PR _j , K) [3, 8, 14, 25] will be random and the number of equations for such a value i such that the left side is zero will tend to N / 2. If the subkey is correctly guessed, the left side will be equal to the fixed bit K3 with probability 12/64 [26]. Those. there will be a significant deviation from N / 2.

Having received 6 bits of the K1 subkey, you can similarly open 6 bits of the K3 subkey. All that is needed for this is to replace C in the equation (6) with P and K1 with K3:
PL [3, 8, 14, 25] ⊕ PR [17] ⊕ CL [3, 8, 14, 25] ⊕ F3 (CR, K3) [3, 8, 14, 25] = K1 [26] .
Algorithm 2 will return the correct K3 value [25 ~ 30] because the DES decryption process is identical to the encryption process, just the key sequence is reversed. So in the first round of decryption the key K3 is used, and in the last one the key K1.

After receiving 6 bits of the K1 and K3 subkeys, the attacker recovers 12 bits of the K key shared key, since round keys are the usual permutation of the key K. The number of open texts required for a successful attack depends on the probability of a statistical counterpart. To open 12 bits of a 3-round DES key, 100 pairs of open / closed texts are enough. To open 12 bits of a 16-round DES key, about 2 ⁴⁴ pairs of text are required. The remaining 44 bits of the key are opened by normal brute force.

Links

Mitsuru Matsui - Linear cryptanalysis method of DES cipher
Tutorial on Linear and Differential Cryptanalysis