Why can not divide by zero, even if you really want?
Recently, an amazing article appeared on Habré, “Dad, why can't you divide by zero?”, Which gathered a lot of equally amazing comments.
Children's questions are usually very complex (“Why is the sky dark at night?”, “Why do apples fall to the ground?”) And adults usually do not have enough time to explain them lucidly. And adults do not always know the answer to these questions.
However, the question of dividing by zero is never one of the complex issues, and it remains a mystery to me why so many problems arise with it. Probably due to some flaws in the methods of teaching mathematics in high school, in the difficulties of the transition from the study of arithmetic to the study of alphabetic algebra and the properties of elementary functions.
')
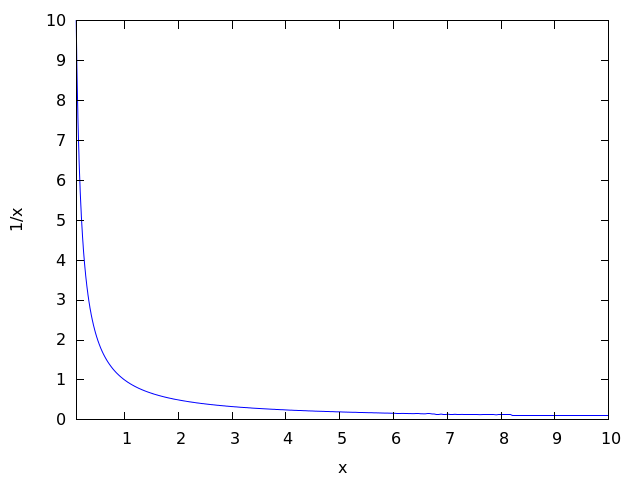
The most serious doubts arise, I think, after studying rational numbers, when for any number x, except zero, the concept of the inverse number 1 / x is introduced, and the hyperbola graph y (x) = 1 / x.
Obviously, when dividing 1 into very small numbers, very large numbers appear, and the less we take x, the more it becomes 1 / x. Why can we not say that 1 / x = ∞ is a certain number?
The algebraic objection to this is as follows. Suppose that ∞ = 1 / x is a number. Then this number should apply to all the rules that exist for ordinary numbers. In particular, on the one hand, the relation 0⋅∞ = 1 must be true, and on the other hand, since 0 = 1−1, 0⋅∞ = 1⋅∞ − 1⋅∞ = 0. Thus, we have 1 = 0, and from this it follows that all numbers are equal to each other and equal to zero. Indeed, since for any x the number 1⋅x = x is true, then 1⋅x = 0⋅x = 0.
“Well, isn't that complete nonsense?” - we ask ourselves, having reached this place.
Of course, this is complete nonsense, if we are talking about ordinary numbers. But it is not for nothing that I emphasized the word “rules” above. We will return to them a little later, after considering the arithmetic objection against division by zero, and will help us in this bean.
Let's go back to the times when there were no computers, no calculators, or slide rules, and set ourselves the task of dividing a random number, for example, by 5.
To do this, take a bowl with beans, symbolizing the natural row, and pour out of it a certain number of grains on a lined sheet of paper:

Thereby, we set the dividend on our bean calculator.
The challenge is to decompose these grains into five rows. In order not to get confused, we mark these rows, that is, set the divisor:

Now we spread the grain from the heap into five rows in a column. This is much longer than on a regular calculator, but it allows you to feel the beauty of arithmetic before the invention of the positional number system.

The algorithm ends when we get some rectangular number and (possibly) a remainder:

In this example, 2 grains remained, and rows of 5 grains formed 18. It turns out that the random number was 18⋅5 + 2 = 92.
It is clear that we can perform this algorithm for any natural divisible and any natural divisor other than zero; if the divisor is 0, then this algorithm is simply impossible to perform.
“Wait!” The attentive reader will say. - "In the above example, we got the rest 2, what to do with it?"
This is, in fact, a very important point. Generally speaking, we cannot divide the beans, without spoiling our bean calculator - not only is it difficult to divide 2 beans into 5 equal parts, even if we smash them properly, we will not be able to assemble them.
Therefore, for a long time, people tried to do without fractions. For example, the following problem is described in an anonymous Arabic manuscript of the 12th century: “divide 100 pounds between 11 people”. Since 100 = 11⋅9 + 1, the medieval mathematician proposes to first distribute 9 pounds to each, and then exchange the remaining pound for eggs, which, as it turns out at the exchange rate, get exactly 91. But 91 = 11⋅8 + 3, therefore Arab the scientist proposes to distribute 8 eggs each, and give the three remaining eggs to the one who produces the section, or exchange them for salt to the eggs.
Speaking in modern mathematical language, the division was carried out in the semiring of natural numbers. However, with the same success, using red and white beans, we could define division with the remainder and in the ring of integers - in the above algorithm there would appear additional rules for choosing the colors used to calculate the beans, but the operations would also be meaningless. x / 0 and 5/2.
Obviously, in order to give the symbol 5/2 a specific meaning, you need to change the rules of the game, and go to the field of rational fractions, adding to the set of integers with all sorts of expressions m / n, where m is integer and n is natural.
It is important to note that this can be done in a not unique way, but in classical arithmetic there is considered a completion in which the symbol 1 / n means the fraction from dividing 1 by n, i.e., a number for which the expression n /1 / n = one; where shares do not make sense when counting piece objects (for example, beans), but when measuring quantities that are assumed to be continuous (or at least unboundedly divisible) - lengths of segments, areas of figures, etc.
In the field of rational fractions it makes no sense to consider the incomplete quotient and residuals, since the quotient of any nonzero divisor is some kind of rational fraction. Moreover, as is the case with natural numbers, we can use beans to divide without changing the algorithm.
Indeed, suppose you want to divide the rational number α = p / q by β = r / s. This is equivalent to performing the following actions:
α: β = p / q: r / s = p⋅s / q⋅r
and the problem for any rational α and β has been reduced to the already known procedure for dividing integers. This again shows that the division by zero has no arithmetic meaning.
“It turns out that it’s impossible to divide by zero, even if you really want to?” - alas, the answer to this question is positive: we cannot determine the division by zero operation based on their natural counting and measurement needs. True, there are two loopholes.
First, instead of “ordinary” numbers (i.e., the rings of naturals and rational fields, as well as the field of real numbers, which I, by the way, have not said a word so far and will tell you some other time), consider a degenerate case - trivial ring {0}, and put by definition 0/0 = 0. In this case, when we are told: “All numbers are equal to each other and are equal to zero!” - we can say in an unabashed tone: “So what? It has always been like this. ”
The second is to abandon some of the usual rules of multiplication. In particular, from the axiom 0⋅x = 0. It is said that this is possible (see http://en.wikipedia.org/wiki/Wheel_theory ). Of course, this option is much more interesting than the first one, but it also represents such a change in the rules of the game, which immediately takes us beyond the framework of classical arithmetic.
In conclusion of this note I want to give a list of references for those who are interested in numerical systems:
- I.V. Arnold Theoretical Arithmetic, M, OGIZ 1938 - a very detailed and detailed book, in which you can find descriptions of classical numerical systems, including quaternions.
- E. G. Gonin "Theoretical Arithmetic", M, 1959 - this book is shorter and more modern, and is also very good, although not as detailed as the book by I.V. Arnold.
- S. Feferman "Numerical Systems" - a classic monograph, sometimes quite complicated; It presents some specific issues that are not in the other two books on theoretical arithmetic.
- A. A. Kirillov “What is a number?” (1993) is a small brochure designed for a prepared reader.
- E. B. Dynkin, V. A. Uspensky “Mathematical Conversations” is a popular book designed for schoolchildren. Contains a lot of information and tasks on such a "non-standard" topic as p-adic numbers.
Children's questions are usually very complex (“Why is the sky dark at night?”, “Why do apples fall to the ground?”) And adults usually do not have enough time to explain them lucidly. And adults do not always know the answer to these questions.
However, the question of dividing by zero is never one of the complex issues, and it remains a mystery to me why so many problems arise with it. Probably due to some flaws in the methods of teaching mathematics in high school, in the difficulties of the transition from the study of arithmetic to the study of alphabetic algebra and the properties of elementary functions.
')

The most serious doubts arise, I think, after studying rational numbers, when for any number x, except zero, the concept of the inverse number 1 / x is introduced, and the hyperbola graph y (x) = 1 / x.
Obviously, when dividing 1 into very small numbers, very large numbers appear, and the less we take x, the more it becomes 1 / x. Why can we not say that 1 / x = ∞ is a certain number?
The algebraic objection to this is as follows. Suppose that ∞ = 1 / x is a number. Then this number should apply to all the rules that exist for ordinary numbers. In particular, on the one hand, the relation 0⋅∞ = 1 must be true, and on the other hand, since 0 = 1−1, 0⋅∞ = 1⋅∞ − 1⋅∞ = 0. Thus, we have 1 = 0, and from this it follows that all numbers are equal to each other and equal to zero. Indeed, since for any x the number 1⋅x = x is true, then 1⋅x = 0⋅x = 0.
“Well, isn't that complete nonsense?” - we ask ourselves, having reached this place.
Of course, this is complete nonsense, if we are talking about ordinary numbers. But it is not for nothing that I emphasized the word “rules” above. We will return to them a little later, after considering the arithmetic objection against division by zero, and will help us in this bean.
Let's go back to the times when there were no computers, no calculators, or slide rules, and set ourselves the task of dividing a random number, for example, by 5.
To do this, take a bowl with beans, symbolizing the natural row, and pour out of it a certain number of grains on a lined sheet of paper:

Thereby, we set the dividend on our bean calculator.
The challenge is to decompose these grains into five rows. In order not to get confused, we mark these rows, that is, set the divisor:

Now we spread the grain from the heap into five rows in a column. This is much longer than on a regular calculator, but it allows you to feel the beauty of arithmetic before the invention of the positional number system.

The algorithm ends when we get some rectangular number and (possibly) a remainder:

In this example, 2 grains remained, and rows of 5 grains formed 18. It turns out that the random number was 18⋅5 + 2 = 92.
It is clear that we can perform this algorithm for any natural divisible and any natural divisor other than zero; if the divisor is 0, then this algorithm is simply impossible to perform.
“Wait!” The attentive reader will say. - "In the above example, we got the rest 2, what to do with it?"
This is, in fact, a very important point. Generally speaking, we cannot divide the beans, without spoiling our bean calculator - not only is it difficult to divide 2 beans into 5 equal parts, even if we smash them properly, we will not be able to assemble them.
Therefore, for a long time, people tried to do without fractions. For example, the following problem is described in an anonymous Arabic manuscript of the 12th century: “divide 100 pounds between 11 people”. Since 100 = 11⋅9 + 1, the medieval mathematician proposes to first distribute 9 pounds to each, and then exchange the remaining pound for eggs, which, as it turns out at the exchange rate, get exactly 91. But 91 = 11⋅8 + 3, therefore Arab the scientist proposes to distribute 8 eggs each, and give the three remaining eggs to the one who produces the section, or exchange them for salt to the eggs.
Speaking in modern mathematical language, the division was carried out in the semiring of natural numbers. However, with the same success, using red and white beans, we could define division with the remainder and in the ring of integers - in the above algorithm there would appear additional rules for choosing the colors used to calculate the beans, but the operations would also be meaningless. x / 0 and 5/2.
Obviously, in order to give the symbol 5/2 a specific meaning, you need to change the rules of the game, and go to the field of rational fractions, adding to the set of integers with all sorts of expressions m / n, where m is integer and n is natural.
It is important to note that this can be done in a not unique way, but in classical arithmetic there is considered a completion in which the symbol 1 / n means the fraction from dividing 1 by n, i.e., a number for which the expression n /1 / n = one; where shares do not make sense when counting piece objects (for example, beans), but when measuring quantities that are assumed to be continuous (or at least unboundedly divisible) - lengths of segments, areas of figures, etc.
In the field of rational fractions it makes no sense to consider the incomplete quotient and residuals, since the quotient of any nonzero divisor is some kind of rational fraction. Moreover, as is the case with natural numbers, we can use beans to divide without changing the algorithm.
Indeed, suppose you want to divide the rational number α = p / q by β = r / s. This is equivalent to performing the following actions:
α: β = p / q: r / s = p⋅s / q⋅r
and the problem for any rational α and β has been reduced to the already known procedure for dividing integers. This again shows that the division by zero has no arithmetic meaning.
“It turns out that it’s impossible to divide by zero, even if you really want to?” - alas, the answer to this question is positive: we cannot determine the division by zero operation based on their natural counting and measurement needs. True, there are two loopholes.
First, instead of “ordinary” numbers (i.e., the rings of naturals and rational fields, as well as the field of real numbers, which I, by the way, have not said a word so far and will tell you some other time), consider a degenerate case - trivial ring {0}, and put by definition 0/0 = 0. In this case, when we are told: “All numbers are equal to each other and are equal to zero!” - we can say in an unabashed tone: “So what? It has always been like this. ”
The second is to abandon some of the usual rules of multiplication. In particular, from the axiom 0⋅x = 0. It is said that this is possible (see http://en.wikipedia.org/wiki/Wheel_theory ). Of course, this option is much more interesting than the first one, but it also represents such a change in the rules of the game, which immediately takes us beyond the framework of classical arithmetic.
In conclusion of this note I want to give a list of references for those who are interested in numerical systems:
- I.V. Arnold Theoretical Arithmetic, M, OGIZ 1938 - a very detailed and detailed book, in which you can find descriptions of classical numerical systems, including quaternions.
- E. G. Gonin "Theoretical Arithmetic", M, 1959 - this book is shorter and more modern, and is also very good, although not as detailed as the book by I.V. Arnold.
- S. Feferman "Numerical Systems" - a classic monograph, sometimes quite complicated; It presents some specific issues that are not in the other two books on theoretical arithmetic.
- A. A. Kirillov “What is a number?” (1993) is a small brochure designed for a prepared reader.
- E. B. Dynkin, V. A. Uspensky “Mathematical Conversations” is a popular book designed for schoolchildren. Contains a lot of information and tasks on such a "non-standard" topic as p-adic numbers.
Source: https://habr.com/ru/post/233579/
All Articles