Math, STA? !! 1
At the beginning of 2012, a video of the Harry Bernhardt report on CodeMash called “WAT” was online. On Habré there were even two habrastii about this report: one , two . This talk was about some of the subtleties of Ruby and JavaScript, which seem illogical and cause a reaction: “WAT?”.
In the same habrastia, I collected ten examples of mathematical reasoning, which, on the contrary, at first glance seem logical, but seeing the result obtained, I also want to ask myself the question "STA? !!".
So, can you tell where the trick is?
')
1. Everyone at school passes the formula for the sum of the first n members of an arithmetic progression , applying this formula to the sum of the first n positive integers we get:
1 + 2 + 3 + ... + n = n ( n + 1) / 2.
If this formula is applied to the sum of numbers from 1 to n - 1, then we get of course
1 + 2 + 3 + ... + ( n - 1) = ( n - 1) n / 2.
Let's add to both parts of the last equality one by one:
1 + 2 + 3 + ... + ( n - 1) + 1 = ( n - 1) n / 2 + 1.
Simplifying, we get:
1 + 2 + 3 + ... + n = ( n - 1) n / 2 + 1.
What is the sum on the left side of this equation we wrote down at the very beginning, therefore,
n ( n + 1) / 2 = ( n - 1) n / 2 + 1.
We open brackets:
n 2/2 + n / 2 = n 2/2 - n / 2 + 1.
Simplify and get that
n = 1.
Since n was arbitrary, we showed that all positive integers are 1.
2. Consider the integral
.
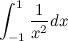Since the function 1 / x 2 is positive throughout its domain of definition, the value of the integral must be positive. Let's check.
The antiderivative of the function 1 / x 2 can be found in the table of primitives and is −1 / x + const.
We use the Newton-Leibniz formula:
.
3. Consider the system of equations
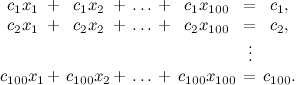
The number of variables coincides with the number of equations, so Kramer’s method is applied , which is that the solution is expressed in the form x k = Δ k / Δ, where Δ is the determinant of the system matrix, and Δ k is the determinant of the matrix obtained from the system matrix replacing the kth column with a column of free members. But the column of free terms coincides with any of the columns of the matrix, so Δ = Δ k . So, x k = 1 for all k . Well, we substitute this solution in the first equation:
Therefore, 100 c 1 = c 1 . Dividing both sides of the equality by c 1 , we get that 100 = 1.
4. Consider a series
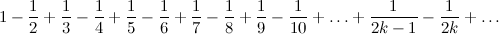
This is the so-called alternating harmonic series , it converges, and its sum is equal to ln 2.
Rearrange the members of this series so that one positive member is followed by two negative ones:
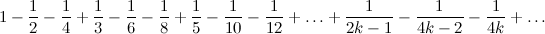
It seems that nothing terrible happened, the series both converged and converged, but let's consider a subsequence of partial sums of this series:
.
The last sum is nothing more than the sum of the first 2 m members of the original alternating harmonic series, the sum of which, as we remember, is equal to ln 2. And this means that the sum of the series with the transposed members is ½ln 2.
5. We turn to the limits. Consider the limit
.
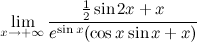Since the numerator and denominator tend to infinity as x tends to infinity, and the numerator and denominator are differentiable, we can apply the L'Hôpital rule.
Find the derivative of the numerator:
(½sin2 x + x ) '= cos2 x + 1 = 2cos 2 x .
Find the derivative of the denominator:
(e sin x (cos x sin x + x )) '= e sin x cos x (cos x sin x + x ) + e sin x (−sin 2 x + cos 2 x + 1) = e sin x cos x (cos x sin x + x + 2cos x ).
From where
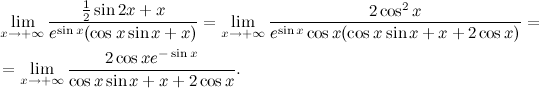
Now we note that the numerator is a bounded function, and the denominator tends to plus infinity as x tends to plus infinity, so the limit is 0.
If you have not noticed anything unusual, then let's rewrite the denominator in the original limit as follows:
e sin x (cos x sin x + x ) = e sin x (½ sin 2x + x ).
Therefore, the numerator and denominator of the original function can be simply reduced by ½sin 2x + x , therefore, the function under the limit sign is simply equal to e −sin x . And such a function already has no limit when x tends to plus infinity!
6. Here is another limit:
.
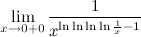Let's look at the graph of the function under the sign of the limit:
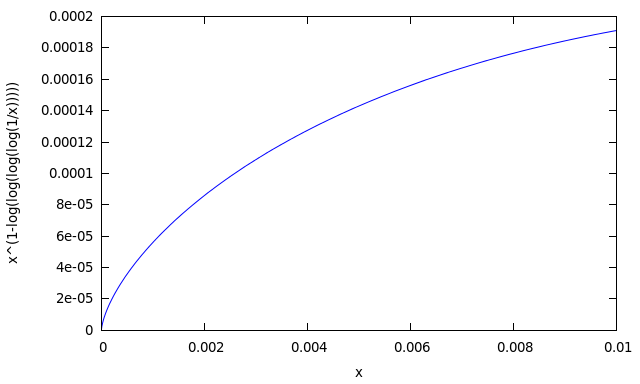
It can be seen that the function with x tending to zero on the right tends to zero. Let's count for certainty several values:
So the limit is probably 0. Do you agree? We calculate symbolically:
Got plus infinity! And this is the correct answer.
7. Consider the matrix
.
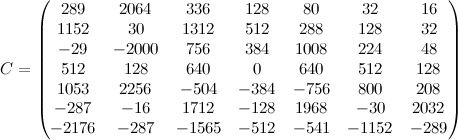We use some mathematical package to find its own numbers. I had Maxima on hand, so I took advantage of her :
That is, we got approximately the following eigenvalues:
−5.560, 5.064 + 1.892 i , 5.064 - 1.892 i , 1.156 + 4.316 i , 1.156 - 4.316 i , −3.440 + 3.327 i , −3.440 - 3.327 i .
Well, numbers are like numbers, but let's also find the eigenvalues of the transposed matrix, we expect to get the same numbers, since the eigenvalues of the matrix during transposition do not change.
That is, the eigenvalues of the transposed matrix are approximately as follows:
−8.318, 7.570 + 3.333 i , 7.570 - 3.333 i , 1.804 + 7.453 i , 1.804 - 7.453 i , −5.215 + 5.891 i , −5.215 - 5.891 i .
No coincidence! But let's go ahead and find the eigenvalues symbolically:
This time we got −1, 1, −2, 2, −4, 4, 0.
8. Consider equality, which some consider the most beautiful in mathematics:
e i π + 1 = 0.
Rewrite it as
e i π = −1.
By squaring both sides of the equality, we get
e 2 i π = 1.
And now we will raise both sides of the last equality to the power of i :
(e 2 i π ) i = 1 i .
We know that 1 is 1 to any degree, so
e 2 i 2 π = 1.
But we also know that i 2 = −1, therefore
e −2π = 1.
Here you can take a calculator just in case and make sure that e −2π is still approximately equal to 0.001867442731708, which is certainly not 1.
9. Consider a stepped plate of infinite length consisting of rectangles: the first rectangle is a square with dimensions of 1 cm by 1 cm, the second is a rectangle with dimensions of 0.5 cm by 2 cm, each next rectangle is twice as long and twice the previous one, then ie, it has dimensions of 2 k −1 by 2 1− k cm. Note that the area of each rectangle is equal to one square centimeter, therefore the area of the whole plate is infinite. Therefore, to paint this plate will require an infinite amount of paint.
Consider a vessel consisting of cylinders. The height of the first cylinder is 1 cm, the radius is also 1 cm, the height of the second cylinder is 2 cm, the radius is 0.5 cm, and so on, each next cylinder is also twice as long as the previous one, and its radius is two times smaller.
Let us find the volume of this vessel: the volumes of the cylinders form a geometric progression: π, ½π, ¼π, ..., π / 2 k , ... Therefore, the total volume is finite and equals 2π cubic centimeters.
Fill our vessel with paint. We will lower our plate into it and pull it out. It will be completely painted with the final amount of paint from all sides!
10. And finally, we prove the following statement:
All horses are white.
For the proof, we use induction.
Base induction. Obviously, there are horses in white. Choose one of these horses.
Induction step. Let it be proved that any k horses are white. Consider a set of k + 1 horses. Remove from this set one horse. The remaining k horses will be white by the induction hypothesis. Now we will return the cleaned horse and remove some other one. The remaining k horses will be white again by the induction hypothesis. Therefore, all k + 1 horses will be white.
It follows that all horses are white. Q.E.D.
If you still want to look for errors in reasoning, then I recommend the book S. Klymchuk, S. Staples, "Paradoxes and Sophisms in Calculus".
In the same habrastia, I collected ten examples of mathematical reasoning, which, on the contrary, at first glance seem logical, but seeing the result obtained, I also want to ask myself the question "STA? !!".
So, can you tell where the trick is?
')
1. Everyone at school passes the formula for the sum of the first n members of an arithmetic progression , applying this formula to the sum of the first n positive integers we get:
1 + 2 + 3 + ... + n = n ( n + 1) / 2.
If this formula is applied to the sum of numbers from 1 to n - 1, then we get of course
1 + 2 + 3 + ... + ( n - 1) = ( n - 1) n / 2.
Let's add to both parts of the last equality one by one:
1 + 2 + 3 + ... + ( n - 1) + 1 = ( n - 1) n / 2 + 1.
Simplifying, we get:
1 + 2 + 3 + ... + n = ( n - 1) n / 2 + 1.
What is the sum on the left side of this equation we wrote down at the very beginning, therefore,
n ( n + 1) / 2 = ( n - 1) n / 2 + 1.
We open brackets:
n 2/2 + n / 2 = n 2/2 - n / 2 + 1.
Simplify and get that
n = 1.
Since n was arbitrary, we showed that all positive integers are 1.
SHTA? !!! 1
Actually this equality is wrong:
1 + 2 + 3 + ... + ( n - 1) + 1 = 1 + 2 + 3 + ... + n .
It will become noticeable if instead
1 + 2 + 3 + ... + ( n - 1)
write
1 + 2 + 3 + ... + ( n - 3) + ( n - 2) + ( n - 1).
Then
1 + 2 + 3 + ... + ( n - 3) + ( n - 2) + ( n - 1) + 1 = 1 + 2 + 3 + ... + ( n - 3) + ( n - 2) + n ,
which of course is not equal
1 + 2 + 3 + ... + n .
1 + 2 + 3 + ... + ( n - 1) + 1 = 1 + 2 + 3 + ... + n .
It will become noticeable if instead
1 + 2 + 3 + ... + ( n - 1)
write
1 + 2 + 3 + ... + ( n - 3) + ( n - 2) + ( n - 1).
Then
1 + 2 + 3 + ... + ( n - 3) + ( n - 2) + ( n - 1) + 1 = 1 + 2 + 3 + ... + ( n - 3) + ( n - 2) + n ,
which of course is not equal
1 + 2 + 3 + ... + n .
2. Consider the integral
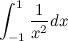.Since the function 1 / x 2 is positive throughout its domain of definition, the value of the integral must be positive. Let's check.
The antiderivative of the function 1 / x 2 can be found in the table of primitives and is −1 / x + const.
We use the Newton-Leibniz formula:
.Not a very positive number!
First, the Newton-Leibniz formula is applicable only if the integrand is continuous on a given segment. Our function at zero has a discontinuity of the second kind and is not bounded on the interval [−1, 1]. (Instead of continuity, you can require the performance of weaker properties, but in any case, the formula will not work.)
3. Consider the system of equations
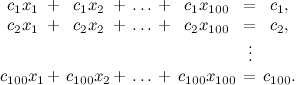
The number of variables coincides with the number of equations, so Kramer’s method is applied , which is that the solution is expressed in the form x k = Δ k / Δ, where Δ is the determinant of the system matrix, and Δ k is the determinant of the matrix obtained from the system matrix replacing the kth column with a column of free members. But the column of free terms coincides with any of the columns of the matrix, so Δ = Δ k . So, x k = 1 for all k . Well, we substitute this solution in the first equation:
Therefore, 100 c 1 = c 1 . Dividing both sides of the equality by c 1 , we get that 100 = 1.
WAT? !!
The Cramer method is applicable only in the case when the determinant Δ is nonzero. In this case, it is not.
4. Consider a series
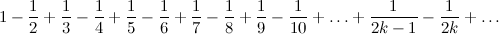
This is the so-called alternating harmonic series , it converges, and its sum is equal to ln 2.
Rearrange the members of this series so that one positive member is followed by two negative ones:
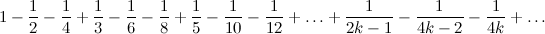
It seems that nothing terrible happened, the series both converged and converged, but let's consider a subsequence of partial sums of this series:
.The last sum is nothing more than the sum of the first 2 m members of the original alternating harmonic series, the sum of which, as we remember, is equal to ln 2. And this means that the sum of the series with the transposed members is ½ln 2.
How did it happen that ln2 = ln2 / 2?
Since the series was conditionally convergent, it is impossible to guarantee that its sum will remain unchanged when the members are rearranged. Moreover, the Riemann theorem states that from this series (and any other conditionally convergent) suitable permutation of terms, one can obtain a series, the sum of which will be any predetermined number, or a divergent series at all.
5. We turn to the limits. Consider the limit
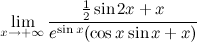.Since the numerator and denominator tend to infinity as x tends to infinity, and the numerator and denominator are differentiable, we can apply the L'Hôpital rule.
Find the derivative of the numerator:
(½sin2 x + x ) '= cos2 x + 1 = 2cos 2 x .
Find the derivative of the denominator:
(e sin x (cos x sin x + x )) '= e sin x cos x (cos x sin x + x ) + e sin x (−sin 2 x + cos 2 x + 1) = e sin x cos x (cos x sin x + x + 2cos x ).
From where
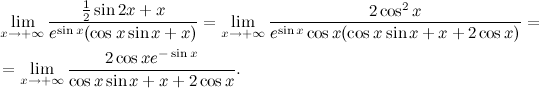
Now we note that the numerator is a bounded function, and the denominator tends to plus infinity as x tends to plus infinity, so the limit is 0.
If you have not noticed anything unusual, then let's rewrite the denominator in the original limit as follows:
e sin x (cos x sin x + x ) = e sin x (½ sin 2x + x ).
Therefore, the numerator and denominator of the original function can be simply reduced by ½sin 2x + x , therefore, the function under the limit sign is simply equal to e −sin x . And such a function already has no limit when x tends to plus infinity!
Hey, why, according to the rule of L'Hospital, did you get 0 ?!
In the formulation of the theorem of L'Hôpital, there is another requirement that the denominator does not turn to 0 in some punctured neighborhood of the point at which we consider the limit. Here this requirement is not met.
I took this example from D. Gruntz’s dissertation, On the Computing Limits in a Symbolic Manipulation System.
I took this example from D. Gruntz’s dissertation, On the Computing Limits in a Symbolic Manipulation System.
6. Here is another limit:
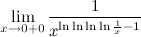.Let's look at the graph of the function under the sign of the limit:
(%i14) plot2d(1/x^(log(log(log(log(1/x)))) - 1), [x, 0, 0.01]); It can be seen that the function with x tending to zero on the right tends to zero. Let's count for certainty several values:
(%i47) f(x) := 1/x^(log(log(log(log(1/x)))) - 1)$ (%i48) f(0.00001); (%o48) 2.7321447178155322E-6 (%i49) f(0.0000000000000001); (%o49) 9.6464144195334194E-13 (%i50) f(10.0^-20); (%o50) 7.8557909648538576E-15 (%i51) f(10.0^-30); (%o51) 1.0252378366509659E-19 (%i52) f(10.0^-40); (%o52) 2.8974935848725609E-24 (%i53) f(10.0^-50); (%o53) 1.4064426717966528E-28 So the limit is probably 0. Do you agree? We calculate symbolically:
(%i59) limit(1/x^(log(log(log(log(1/x)))) - 1), x, 0, plus); (%o59) inf Got plus infinity! And this is the correct answer.
But now you are just fooling me, but I saw the schedule!
Let's take a closer look at the function ln ln ln ln x. This function is increasing, while its limit at plus infinity is plus infinity, but it increases very slowly, for example, it takes the value 10 at x = e e e e 10 , which is approximately equal to 10 10 10 9565.6 . Therefore, the expression ln ln ln ln 1 / x - 1 still tends to infinity as x tends to 0 on the right, and therefore the desired limit is infinity.
I also took this example from D. Gruntz’s dissertation, On the Computing Limits in a Symbolic Manipulation System.
I also took this example from D. Gruntz’s dissertation, On the Computing Limits in a Symbolic Manipulation System.
7. Consider the matrix
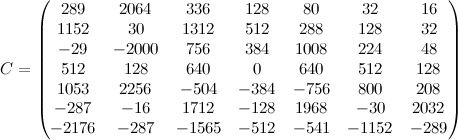.We use some mathematical package to find its own numbers. I had Maxima on hand, so I took advantage of her :
(%i162) load(lapack)$ (%i163) dgeev(C); (%o163) [[1.892759249004818 %i + 5.064646369950517, 5.064646369950517 - 1.892759249004818 %i, 4.316308825205465 %i + 1.156345532561647, 1.156345532561647 - 4.316308825205465 %i, - 5.560325596213962, 3.327556714595323 %i - 3.440829104405306, - 3.327556714595323 %i - 3.440829104405306], false, false] That is, we got approximately the following eigenvalues:
−5.560, 5.064 + 1.892 i , 5.064 - 1.892 i , 1.156 + 4.316 i , 1.156 - 4.316 i , −3.440 + 3.327 i , −3.440 - 3.327 i .
Well, numbers are like numbers, but let's also find the eigenvalues of the transposed matrix, we expect to get the same numbers, since the eigenvalues of the matrix during transposition do not change.
(%i164) dgeev(transpose(C)); (%o164) [[3.333252572558635 %i + 7.570309809213996, 7.570309809213996 - 3.333252572558635 %i, 7.453248893016916 %i + 1.804487379065658, 1.804487379065658 - 7.453248893016916 %i, 5.891112477041645 %i - 5.215502218450374, - 5.891112477041645 %i - 5.215502218450374, - 8.318589939657096], false, false] That is, the eigenvalues of the transposed matrix are approximately as follows:
−8.318, 7.570 + 3.333 i , 7.570 - 3.333 i , 1.804 + 7.453 i , 1.804 - 7.453 i , −5.215 + 5.891 i , −5.215 - 5.891 i .
No coincidence! But let's go ahead and find the eigenvalues symbolically:
(%i166) eigenvalues(C); (%o166) [[- 1, 1, - 2, 2, - 4, 4, 0], [1, 1, 1, 1, 1, 1, 1]] This time we got −1, 1, −2, 2, −4, 4, 0.
I do not understand anything!
In fact, C = L −1 R L , where
,
.
Therefore, the correct answer is: −1, 1, −2, 2, −4, 4, 0.
Numerical methods give incorrect eigenvalues, since this matrix is ill-conditioned with respect to the problem of finding eigenvalues, and because of errors in the calculations, such a large error is obtained.
You can read more about the conditionality number of an eigenvalue, for example, in J. Demmel's book “Computational Linear Algebra”; I would only note that this number is equal to the acute angle secant between the left and right eigenvectors of this eigenvalue.
I took this matrix example from the presentation of S. K. Godunov “Paradoxes of computational linear algebra and spectral portraits of matrices”.
, .Therefore, the correct answer is: −1, 1, −2, 2, −4, 4, 0.
Numerical methods give incorrect eigenvalues, since this matrix is ill-conditioned with respect to the problem of finding eigenvalues, and because of errors in the calculations, such a large error is obtained.
You can read more about the conditionality number of an eigenvalue, for example, in J. Demmel's book “Computational Linear Algebra”; I would only note that this number is equal to the acute angle secant between the left and right eigenvectors of this eigenvalue.
I took this matrix example from the presentation of S. K. Godunov “Paradoxes of computational linear algebra and spectral portraits of matrices”.
8. Consider equality, which some consider the most beautiful in mathematics:
e i π + 1 = 0.
Rewrite it as
e i π = −1.
By squaring both sides of the equality, we get
e 2 i π = 1.
And now we will raise both sides of the last equality to the power of i :
(e 2 i π ) i = 1 i .
We know that 1 is 1 to any degree, so
e 2 i 2 π = 1.
But we also know that i 2 = −1, therefore
e −2π = 1.
Here you can take a calculator just in case and make sure that e −2π is still approximately equal to 0.001867442731708, which is certainly not 1.
And this time what's the catch?
In fact, the function of raising to a complex degree is multivalued and, for example,
1 i = {e −2π k | k ∈ Z }.
And so the fourth junction is no longer true. If you consider only one of the branches, then some of the usual identities for the degrees cease to hold, which is what happened here.
1 i = {e −2π k | k ∈ Z }.
And so the fourth junction is no longer true. If you consider only one of the branches, then some of the usual identities for the degrees cease to hold, which is what happened here.
9. Consider a stepped plate of infinite length consisting of rectangles: the first rectangle is a square with dimensions of 1 cm by 1 cm, the second is a rectangle with dimensions of 0.5 cm by 2 cm, each next rectangle is twice as long and twice the previous one, then ie, it has dimensions of 2 k −1 by 2 1− k cm. Note that the area of each rectangle is equal to one square centimeter, therefore the area of the whole plate is infinite. Therefore, to paint this plate will require an infinite amount of paint.Consider a vessel consisting of cylinders. The height of the first cylinder is 1 cm, the radius is also 1 cm, the height of the second cylinder is 2 cm, the radius is 0.5 cm, and so on, each next cylinder is also twice as long as the previous one, and its radius is two times smaller.
Let us find the volume of this vessel: the volumes of the cylinders form a geometric progression: π, ½π, ¼π, ..., π / 2 k , ... Therefore, the total volume is finite and equals 2π cubic centimeters.
Fill our vessel with paint. We will lower our plate into it and pull it out. It will be completely painted with the final amount of paint from all sides!
WAT ?!
This is a famous painter's paradox .
When we talked about the impossibility of painting the plate, we assumed that the plate was covered with a layer of paint of the same thickness.
When painting with the help of our vessel, each next rectangle is covered with an increasingly thin layer of paint.
When we talked about the impossibility of painting the plate, we assumed that the plate was covered with a layer of paint of the same thickness.
When painting with the help of our vessel, each next rectangle is covered with an increasingly thin layer of paint.
10. And finally, we prove the following statement:
All horses are white.
For the proof, we use induction.
Base induction. Obviously, there are horses in white. Choose one of these horses.
Induction step. Let it be proved that any k horses are white. Consider a set of k + 1 horses. Remove from this set one horse. The remaining k horses will be white by the induction hypothesis. Now we will return the cleaned horse and remove some other one. The remaining k horses will be white again by the induction hypothesis. Therefore, all k + 1 horses will be white.
It follows that all horses are white. Q.E.D.
But I saw black horses!
Everything is simple : instead of a universal quantifier, the existence quantifier is used in the base of induction.
If you still want to look for errors in reasoning, then I recommend the book S. Klymchuk, S. Staples, "Paradoxes and Sophisms in Calculus".
Source: https://habr.com/ru/post/232007/
All Articles