Hedgehog in fractal fog

This article is the last of my fractal series. In Habrastier "Drawing pictures with the Hilbert Curve," it was told about a kitten named Gav, in Habrastier "Kosh on a complex plane" - about the flow of fractals into the horizon, in Habrastier " Fractals Night" about the escape time algorithm. In this article we will talk about a hedgehog in the fog and, of course, about the cat.




')
Anyone who has ever experienced a bit of fractals has seen beautiful pictures of Julia sets, which are defined by a square polynomial; but it is interesting to solve the inverse problem: let there be some picture, and we go over it to come up with such a polynomial, which will give some approximation of the original picture. A picture with a hedgehog above demonstrates this idea.

So, consider the cat K.



We need to come up with a polynomial f such that inside a cat the sequence f ( z ), f ( f ( z )), f ( f ( f ( z ))), ... is bounded, and outside the cat it tends to infinity. For a long time I did not think about this question, but immediately looked on the Internet and found a wonderful article by Kathryn A. Lindsey , “Shapes of polynomial Julia sets” , 2013, arXiv: 1209.0143 . This article proves that for a “good” cat and for a given accuracy δ, such a polynomial can be invented, and the proof is constructive.

Consider this design. Let φ 'be a conformal mapping that the exterior of the unit circle translates into the exterior of a cat. Let φ ( z ) = φ '((1 + ε) z ) be the original map corrected to some small ε.



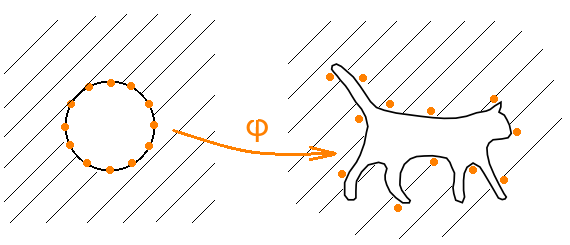
Further, let ω ( z ) = c ^{- n} ( z - r ₀ ) ( z - r ₁ ) ⋅… ⋅ ( z - r _{n −1} ), where c is the coefficient at z in the expansion of the map φ in the Laurent series, and r _k = φ (e ^{2π ik / n} ) are images of roots of unit nth degree. It is proved that the polynomial f ( z ) = z (ω ( z ) + 1) is the desired one for sufficiently large n .

Therefore, to solve our problem, it is necessary to learn how to generate the corresponding conformal mapping. As a result of a small search on the Internet, the zipper package was found. This package allows you to find a conformal mapping of the interior of the unit circle to the area bounded by the polyline. Although this package was written twenty years ago in an ancient dialect , it was not difficult to assemble it and use it.



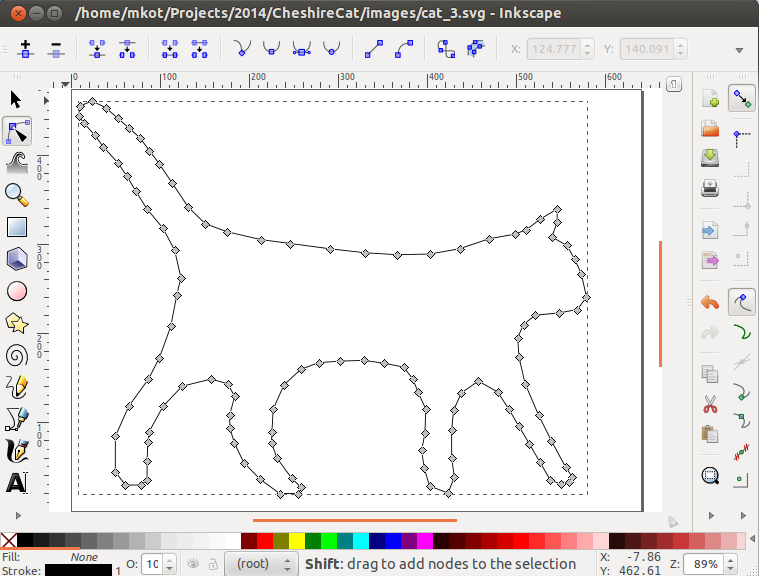
To use this package, you need to build a broken line in the image. I didn’t do some kind of automatic solution, but loaded the image into Inkscape editor and circled it, and parsing the SVG format is simple. This is convenient in that it allows you to experiment with a polyline.




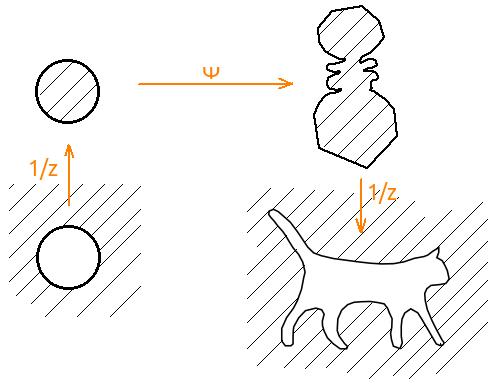
Next, we need a mapping from the exterior to the exterior, and the package finds the mapping from the inside to the inside. Here you just need to pair the generated map with the inverse. That is, φ '( z ) = 1 / (1 / z ), where ψ is the map that generates the packet. And it is necessary to feed the already inverted broken line to the input of the packet.




In the definition of the polynomial f , the coefficient c is also involved. For an approximate calculation of its value, we use the following technique. Let be

f ( z ) = c z + a + a ₁ / z + a ₂ / z ² + a ₃ / z ³ + ...

Consider some finite, but rather large, part of this series. Substitute in a series of values ​​of the roots of units of n -th degree, where n is greater than the number of members of this piece.

f (e ^{2π ik / n} ) = c e ^{2π ik / n} + a + a ₁ e ^{−2π ik / n} + a ₂ e ^{−4π ik / n} + a ₃ e − ^{6π ik / n} + ..., k = 0, ..., n - 1.

Now multiply each line by e ^{−2π ik / n} and add all the lines. Since the sum of all roots of a unit is 0, only n c will remain on the right. Therefore, we can put

c = ( f (1) ⋅ 1 + f (e ^{2π i / n} ) e ^{−2π i / n} +… + f (e ^{2π i ( n - 1) / n} ) e ^{−2π i ( n - 1) / n} )) / n .

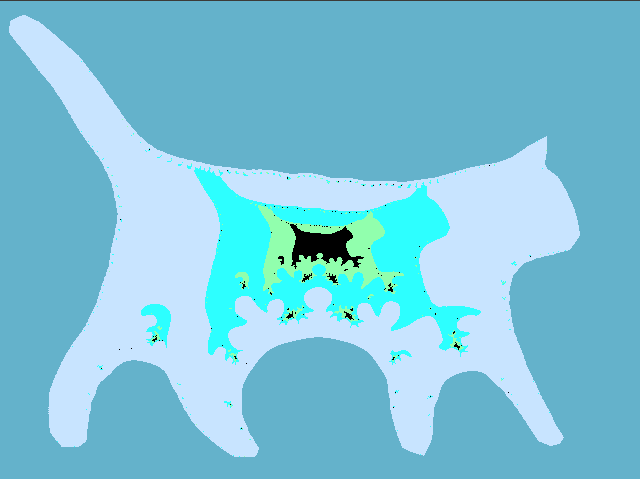
Putting it all together and check what happened. The figure below shows the “thermal” graph of the logarithm of the module f ( z ) (the redder, the greater the value). As you can see, inside the cat the values ​​of the polynomial are small, and outside the cat the polynomial increases, so it should be. Notice also how the values ​​of f (e ^{2π ik / n} ) are distributed (green dots), because of this effect I had to draw a cat whose legs are far enough apart from each other.



Now we simply use some kind of algorithm to draw the Julia set and get a cat whose boundary is fractal.




If our image consists of several areas A ₁ , A ₂ , ..., A _q , then in the above article it is proposed to use instead of a polynomial a rational map f ( z ) defined as follows. For each region _Ar , we write the product ω _r ( z ) as above. Then the desired rational function f ( z ) is defined by the formula f ( z ) = z / (1 / ω ₁ ( z ) +… + 1 / ω _q ( z )).

For example, suppose we have a hedgehog in the fog E.



We will circle the hedgehog and the hill (the lower border of the hill is outside the picture).



Hedgehog in a vacuum.



A hill without a hedgehog.



Together.



Enlarged belly of a hedgehog with fleas, hedgehogs.



As always, the source code can be found on a githaba .

I repeat the link to the article with the help of which everything turned out: Kathryn A. Lindsey , “Shapes of polynomial Julia sets” , 2013, arXiv: 1209.0143 . I note, the article is easy to read, so you can pick up the evidence for a cup of tea.

I hope it was fun.