Looking for a melody by fragment

Greetings, dear readers of Habr!
In this article I want to tell you how I searched for a piece of music based on its passage.
So let's go!
The task in front of me is the following: there is an excerpt of a musical work, there is a base of musical works, and it is necessary to find out which of the available musical works this extract belongs to.
For those interested, read under the harbokat.

I decided that for these purposes I will present music as a function of frequency and time.
For this, I will do the following:

I will cut the signal on the windows, as illustrated in the figure, and I will use a modification of the sliding window algorithm. The modification will consist in the fact that the window will not “smoothly slide” on the signal, but “move on the signal abruptly”, in other words, the windows will overlap.


')
As a window, we take the so-called “Hamming window”.

As a point in time, a component will appear with a certain frequency, we will take a point in time corresponding to the middle of the window. This modification will improve the resolution in the time and frequency domains: in the frequency domain due to a relatively large window, and in the time domain due to the fact that the Hamming window has a relatively narrow main lobe and when moving the window with overlapping, we can fairly accurately record the time samples.

In each window we will perform a Fourier transform, in order to obtain a set of frequencies that are present in this window.
Total for an arbitrary composition, we get the following:

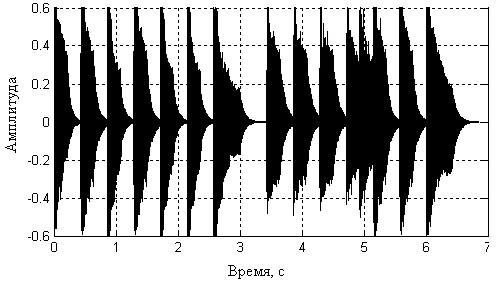
At the entrance - the dependence of the amplitude on time:



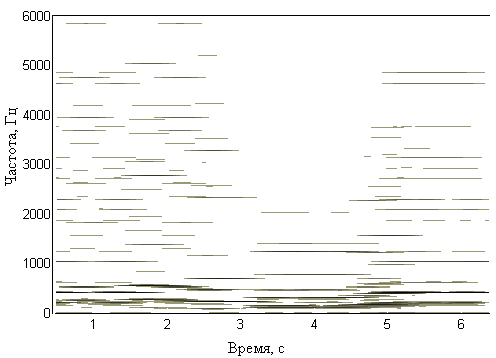
And at the output - dependence of amplitude on frequency:



We do not end there.

After we get the time-frequency representation, we filter out various interferences, and select frequencies that correspond to the notes.
Thereby we get a time-note representation - a function of the note number from time.
But here we are faced with the fact that the same melody can be played from different notes, for example (in figure (a) from a higher note, and in figure (b) - from a lower note):



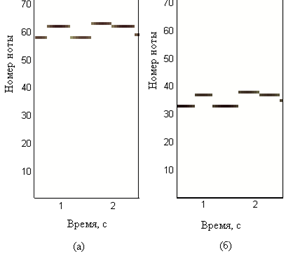
But if we look at the pictures, we will see that the pictures are similar.

Hence the following idea: in order to identify a piece of music regardless of the tonality on which it was played, one should take into account not the absolute values ​​of the numbers of notes and the time of their appearance, but relative ones - the differences between the values ​​of the next and previous readings of the numbers of notes and times.

So, we can get from the time-note function a two-line matrix, in one line of which there will be differences of notes, and in the other line the difference of the times of their appearance, thus, we will take into account the rhythm.

Despite the fact that the works were played on different keys, the following relationship holds true:



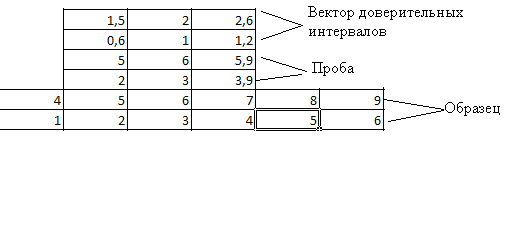
The identification algorithm is as follows:

• the vector of confidence intervals is calculated - the audio imprint of the signal taken as the sample is taken (in this case it is a matrix with two rows and a certain number of columns), and a vector of the same size is calculated, whose elements are equal to thirty percent of the absolute values ​​of the corresponding elements in the sample;
• then a smaller audio imprint moves along a larger audio imprint on the basis of a sliding window. In this case, the difference module of the corresponding elements is considered, and it is checked that this difference is not greater than the corresponding elements of the vector of confidence intervals;

• if this difference is not greater, then the number of columns is considered. satisfying the condition;
• then this number is normalized by the number of columns in the “smaller” audio imprint;
• after that the maximum proportion of similarity is chosen.

And further, if the proportion of similarities in my case is above 75%, then, I believe that the melody is found.