An overview of the available libraries for the numerical solution of rigid ODEs
Creating supplements to the national mathematical program SMath Studio , I found a number of libraries in the network that could be used in my programs. I offer a small review of them.
A standard fixed-pitch RK45 can help in most cases, but there are tasks where this is not enough. To solve rigid systems, special solvers were invented, which we will consider from the point of view of their practical use.
Most of the functions presented below, unless otherwise specified, can be reduced to the same call format (similar to Mathcad):
')
ode_solver( init, x1, x2, intvls, D(t, x) ) Where:
- init is the initial conditions vector,
- (x1, x2) - integration segment,
- intvls - the number of intervals on the segment,
- D (t, x) is an ODE system.
1. Intel ODE Solvers Library
It contains the following functions: rkm9st (), mk52lfn (), mk52lfa (), rkm9mkn (), rkm9mka ().
- rkm9st () - ack a dash OD OD E E OD OD OD OD OD OD OD OD OD OD OD OD 9 9 9 9 9 9 9 9 9 9 9
- mk52lfn (a) - a method of using the junction system for a junction system, it can use the jacobi matrix to find out how to use it.
- mc52lfa () is a method of using the jacobi matrix. This user must provide a routine for this computation.
- rkm9mkn () - a) with a variable or a priori unknown stiffness; automatically selects the Jacobi matrix when necessary.
- rkm9mka () - a) with a variable or a priori unknown stiffness; automatically chooses the explicit or implicit scheme in every step. The Jacobi matrix.
The library is written in C with all the ensuing dependencies. The 32-bit and 64-bit versions of the library are available (libiode_ia32.lib and libiode_intel64.lib).
intel_ode.h
/******************************************************************************* ! INTEL CONFIDENTIAL ! Copyright(C) 2007-2008 Intel Corporation. All Rights Reserved. ! The source code contained or described herein and all documents related to ! the source code ("Material") are owned by Intel Corporation or its suppliers ! or licensors. Title to the Material remains with Intel Corporation or its ! suppliers and licensors. The Material contains trade secrets and proprietary ! and confidential information of Intel or its suppliers and licensors. The ! Material is protected by worldwide copyright and trade secret laws and ! treaty provisions. No part of the Material may be used, copied, reproduced, ! modified, published, uploaded, posted, transmitted, distributed or disclosed ! in any way without Intel's prior express written permission. ! No license under any patent, copyright, trade secret or other intellectual ! property right is granted to or conferred upon you by disclosure or delivery ! of the Materials, either expressly, by implication, inducement, estoppel or ! otherwise. Any license under such intellectual property rights must be ! express and approved by Intel in writing. ! !****************************************************************************** ! ! Header file for Intel(R) ODE Solvers ! !*******************************************************************************/ #ifndef _INTEL_ODE_H_ #define _INTEL_ODE_H_ #ifdef __cplusplus extern "C" { #endif /* __cplusplus */ void dodesol(int*,int*,double*,double*,double*,void*,void*,\ double*,double*,double*,double*,double*,int*,int*); void dodesol_rkm9st(int*,int*,double*,double*,double*,void*,\ double*,double*,double*,double*,double*,int*); void dodesol_mk52lfn(int*,int*,double*,double*,double*,void*,\ double*,double*,double*,double*,double*,int*,int*); void dodesol_mk52lfa(int*,int*,double*,double*,double*,void*,void*,\ double*,double*,double*,double*,double*,int*,int*); void dodesol_rkm9mkn(int*,int*,double*,double*,double*,void*,\ double*,double*,double*,double*,double*,int*,int*); void dodesol_rkm9mka(int*,int*,double*,double*,double*,void*,void*,\ double*,double*,double*,double*,double*,int*,int*); #ifdef __cplusplus } #endif /* __cplusplus */ #endif /* _INTEL_ODE_H_ */ The ODE Solvers add-on demonstrates working with this library from c # code.
References:
1. Intel® Ordinary Differential Equations Solver Library .
2. Sources supplements ODESolvers .
2. GNU Scientific Library (GSL)
It contains the following functions: rk2 (), rk4 (), rkf45 (), rkck (), rk8pd (), rk1imp (), rk2imp (), rk4imp (), bsimp (), msadams (), msbdf ().
Some of them require additional parameters for work (Jacobian). Those that I managed to lead to a general view:
Solvers for Non-Stiff Systems:
- rk2 () - explicit embedded Runge-Kutta (2, 3) method.
- rk4 () - explicit 4th order (classical) Runge-Kutta. Error estimation is carried out by the step doubling method.
- rkf45 () - explicit embedded Runge-Kutta-Fehlberg (4, 5) method.
- rkck () - explicit embedded Runge-Kutta Cash-Karp (4, 5) method.
- rk8pd () - explicit embedded Runge-Kutta Prince-Dormand (8, 9) method.
Rest:
- rk1imp () - Implicit Gaussian first order Runge-Kutta. Euler or backward Euler method. Error estimation is carried out by the step doubling method. This algorithm requires the Jacobian.
- rk2imp () - Implicit Gaussian second order Runge-Kutta. Also known as implicit mid-point rule. Error estimation is carried out by the step doubling method. This stepper requires the Jacobian.
- rk4imp () - Implicit Gaussian 4th order Runge-Kutta. Error estimation is carried out by the step doubling method. This algorithm requires the Jacobian.
- bsimp () - Implicit Bulirsch-Stoer method of Bader and Deuflhard. The method is generally suitable for stiff problems. This stepper requires the Jacobian.
- msadams () - A variable-coefficient linear multistep Adams method in Nordsieck form. Adams-Moulton (corrector methods) P (EC) ^ m functional iteration mode. Method order varies dynamically between 1 and 12.
- msbdf () - A variable-coefficient linear multistep backward differentiation formula (BDF) method in Nordsieck form. BDF formula as corrector. A modified Newton iteration method. Method order varies dynamically between 1 and 5. The method is generally suitable for stiff problems. This stepper requires the Jacobian.
To work with functions, a universal interface is used , where a specific type of solver sets the step function. The GNUScientificLibrary add- on demonstrates working with this library from c # code.
Not so easy to build a library under Windows. I used the instructions from one site, which is now unavailable. However, in the add-on repository you can find 32- and 64-bit versions of the
References:
1. GSL. Ordinary Differential Equations .
2. Sources of supplement GNUScientificLibrary .
3. Matlab C ++ Math Library 2.1 (Win32)
Yes, you can use this old version of run-time libraries for calculations. Moreover, it can be installed along relative paths, i.e. You can simply put the contents of the original distribution (~ 28 MB in expanded form) next to your program. However, when calling functions, you will have to use SetCurrentDirectory () with a direct reference to the location of the "bin \ win32". I do this in my supplement.
It contains the following functions: ode23 (), ode45 (), ode113 (), ode15s (), ode23s ().
- ode23 () - solve nonstiff differential equations; low order method
- ode45 () - solve nonstiff differential equations; medium order method
- ode113 () - solve nonstiff differential equations; variable order method
- ode15s () - solve stiff differential and DAEs; variable order method
- ode23s () - solve stiff differential; low order method.
The MatlabCppMathLibrary add- on demonstrates working with this library from c # code.
References:
1. Ordinary Differential Equations .
2. MATLAB C ++ Math Library. User's Guide. Version 2.1 (pdf).
3. MATLAB C ++ Math Library. Reference. Version 2 (pdf).
4. MatlabCppMathLibrary add-on sources .
4. Octave C ++ Math Library (Win32)
Approximately the same as Matlab C ++ Math Library, but with its own cockroaches. Unfortunately, I only partially overcame my work with this library. The OctaveCppMathLibrary add- on demonstrates working with this library from c # code.
References:
1. Ordinary Differential Equations .
2. The sources of the OctaveCppMathLibrary add- on .
5. DotNumerics
It contains the following functions: AdamsMoulton (), ExplicitRK45 (), ImplicitRK5 (), GearsBDF (). This library is ported to .Net from Fortran. I liked her the most. It works quite quickly.
Solvers for Non-Stiff Systems:
- AdamsMoulton () solves an initial-value problem for the nonstiff ordinary differential equations using the Adams-Moulton method.
- ExplicitRK45 () - solves an initial-value problem for the nonstiff ordinary (4) 5.
Solvers for Stiff Systems:
- ImplicitRK5 () - Runge-Kutta method of order 5.
- GearsBDF () - solves an initial-value problem for the ordinary differential differential equations using the BDF method.
There are many overloads for various function call formats. DotNumerics add- on demonstrates working with this library.
References:
1. DotNumerics .
2. Sources supplement DotNumerics .
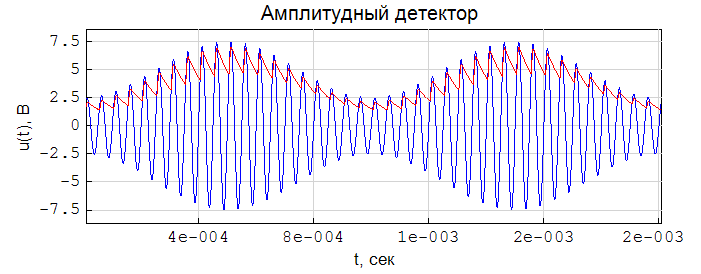
How does the amplitude detector model look like in SMath Studio when solving an ODE using the GearsBDF () function:
SMath Studio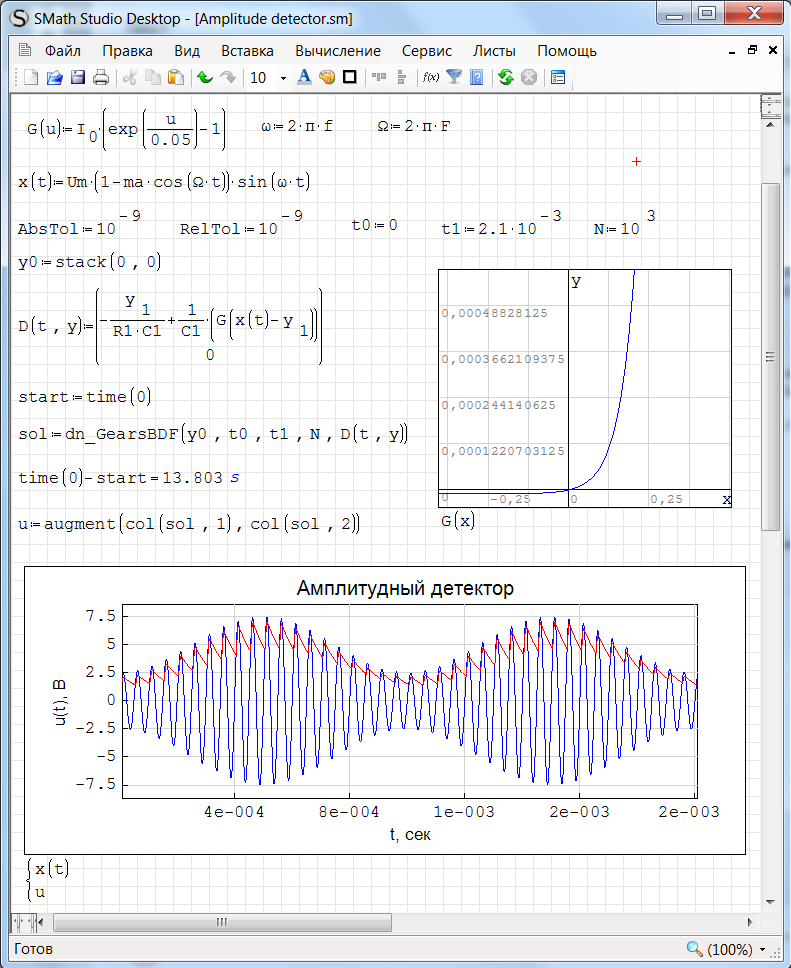

Update (07/12/2014).
6. boost :: odeint
It contains the following algorithms:
- Explicit Euler
- Modified Midpoint
- Runge-Kutta 4
- Cash-Karp
- Dormand-Prince 5
- Fehlberg 78
- Adams bashforth
- Adams moulton
- Adams bashforth moulton
- Controlled Runge-Kutta
- Dense Output Runge-Kutta
- Bulirsch-stoer
- Bulirsch-Stoer Dense Output
- Implicit euler
- Rosenbrock 4
- Controlled Rosenbrock 4
- Dense Output Rosenbrock 4
- Symplectic euler
- Symplectic RKN McLachlan
- Symplectic RKN McLachlan
Live did not try, I can not show an example of use.
References:
1. Boost.Numeric.Odeint .
2. Stepper overview .
7. SADEL (Sets of Algebraic and Differential Equations solvers Library)
Live did not try, I can not show an example of use.
References:
1. About the library SADEL .
2. Comparison of modern solvers of rigid systems of ordinary differential equations with the C solvers of the SADEL library .
8. Solver A. G. Limonov
Live did not try, I can not show an example of use.
References:
1. Thesis. Development of two-stage Rosenbrock schemes with complex coefficients and their application in problems of modeling the formation of periodic nanostructures, 2010 .
Source: https://habr.com/ru/post/229435/
All Articles