10 interesting tasks

Illustration to the last task.
There are problems with simple and seemingly obvious solutions, which, however, are difficult to find. When solving them, it is dangerous to rely on intuition, because the correct answer often does not at all coincide with the one it suggests. In this article, I offer a selection of 10 such tasks, ordered by increasing complexity; Their solutions are removed under the spoiler. To get the right answers you do not need to have any special knowledge, it is enough just resourcefulness and knowledge of the school program.
')
- From the cities A and B, the distance between which is 100 km, at the same time two trains go towards each other, their speeds are 40 km / h and 60 km / h, respectively. At the same time, a fly flies from city A in direction B, flies at a speed of 200 km / h, flies before meeting a train leaving B, then flies to a train that leaves A, then flies again to a train that leaves B, and so on. d. What distance will the fly fly before the trains meet?DecisionThe speed of convergence of trains is 100 km / h, the distance between them is 100 km, which means they will meet in 1 hour. The fly will fly during this hour at a speed of 200 km / h and fly a total of 200 km .
- In a triangle ABC, the angle C is straight, BM is the median. Prove: ∠CAB> ∠ABM.
 EvidenceIn the triangle MBC, the CM legs are smaller than the hypotenuse BM. MC = AM. Hence, MB> AM. Consider the triangle ABM, in it the side MB is greater than the side AM. And on the opposite side of the larger side lies a larger angle. This means ∠CAB> ∠ABM. CTD.
EvidenceIn the triangle MBC, the CM legs are smaller than the hypotenuse BM. MC = AM. Hence, MB> AM. Consider the triangle ABM, in it the side MB is greater than the side AM. And on the opposite side of the larger side lies a larger angle. This means ∠CAB> ∠ABM. CTD. - Citizens of a certain country have been living according to the following rules for a very long time: a family produces children to the first boy, after which children are not born in the family. Only boys and girls are born with equal probabilities; twins are not born. Determine the proportion of male population in this country. Assume that mortality does not depend on gender.DecisionA trap task. The rule “there is exactly one boy in a family” does not affect the probability of having a boy as a whole in the country. The correct answer is 50% .
- Two girlfriends at the same time begin to do homework, and each of them solves seven tasks per hour with Reshebnik, and without it only four. Which of the girls will be released earlier, if the first schoolgirl gave Reshebnik to her friend after completing half of the assignment?DecisionSuppose that the entire task consists of 28 tasks. Half of the task (14 tasks) will be solved by the first one with Reshebnik for 14/7 = 2 hours, and the second one during this time will solve 2 * 4 = 8 tasks. Armed with Reshebnik, the second will solve the remaining 28-8 = 20 tasks in 20/7 <3 hours, and the first during this time will solve only 3 * 4 = 12 tasks, and all she has left is 14 tasks. Consequently, the second girl will cope with the task earlier.
- Scrap iron lies on a piece of ice that floats in the pool. How will the water level in the pool change when the ice melts (and the scrap sinks)?DecisionWe recall the law of Archimedes: on a body immersed in a fluid, a pushing force acts, equal to the force of gravity of the fluid displaced by this body. It should be noted that the body must be completely surrounded by liquid or intersect with the surface of the liquid. For example, Archimedes' law cannot be applied to scrap, which lies at the bottom of the basin. Thus, while ice and scrap float, the mass of scrap and ice is equal to the mass of water displaced. When scrap reaches the bottom, the volume of water displaced by it is equal to the volume of scrap. The mass of ice is equal to the mass of water, which it turned into when it melted, so the contribution of ice can be ignored. (By the way, for the same reason, if the scrap did not appear in the original task, the answer would be that the water level would not change.) Before melting, scrap crowded out more water than after melting, since water has a lower density than scrap. Answer: the water level in the pool will go down . (If we assume that the ice and scrap floated in the water column, and not on the surface, the justification is quite simple: the ice volume decreased when the ice melted, and the scrap volume did not change.)
- The number n is natural, the number p is simple, to prove:
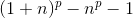 is divisible by p. (You need to know the basics of combinatorics.)EvidenceRecall Newton's bin .
is divisible by p. (You need to know the basics of combinatorics.)EvidenceRecall Newton's bin .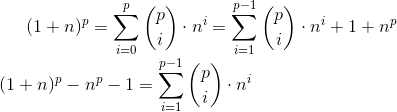
In the last expression, each binomial coefficient is divided by p, since p is simple and is in the numerator in the formula of the binomial coefficient , and in the denominator - the product of numbers less than p. CTD. - The “Tower of Hanoi” puzzle consists of three rods numbered 1, 2, 3. A pyramid of N disks of different diameters is worn on rod 1 in increasing order of diameter. Disks can be shifted from one rod to another one by one, while the disc cannot be placed on a disk of smaller diameter. It is necessary to shift the entire pyramid from rod 1 to rod 3.
Decision
ejudge solution check - How many different lines of length N exist, consisting of the characters "0" and / or "1" in which two units do not go in a row? The answer may be a recurrent formula.DecisionDenote by F (N) the number of rows of length N, not containing two units in a row. Denote by F0 (N) the number of rows of length N, which do not contain two units in a row and end with 0. Denote F1 (N) the number of rows of length N, which do not contain two units in a row and end with 1.
We derive the recurrence formulas for F0 and F1.
F1 (N) = F0 (N-1). Since two units cannot go in a row, the number of lines ending in 1 is equal to the number of lines 1 shorter, ending in 0.
F0 (N) = F0 (N-1) + F1 (N-1). Zero can be added to any valid line, without violating the conditions. This means that the number of lines ending in 0 is equal to the number of lines in 1 shorter.
F0 (N) = F0 (N-1) + F1 (N-1) = F0 (N-1) + F0 (N-2). So, F0 is a Fibonacci series with a certain shift. F1 (N) = F0 (N-1), then F1 also consists of Fibonacci numbers, with a “lag” of 1 relative to F0.
F (N) = F0 (N) + F1 (N). The F (N) term is obtained when a Fibonacci number F0 is added to a Fibonacci number F1, which is the previous number for it. And the sum of the Fibonacci number with the previous Fibonacci number is also the Fibonacci number (according to the formula of Fibonacci numbers). So, we have proven that the number of rows that do not include two units in a row will be the Fibonacci number . It remains to determine the value of F (N) for the first two N. F (1) = 2 (two suitable sequences: "0" and "1"), F (2) = 3 (three suitable sequences: "00", "01" , "ten").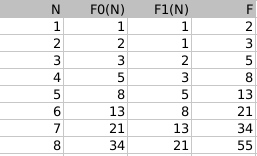
- Shareholders sat down at a round table on which signs with their names were installed (there is one sign for each shareholder). However, everyone sat down at the name plate. Prove that you can turn the table so that at least 2 shareholders sat at their own signs.EvidenceThe key condition is the fact that at the beginning no shareholder sits behind his sign. Let the number of shareholders be equal to N. The number of table states is also N. On one of the table states (initial) no shareholder sits at his plate, therefore the table conditions at which comparisons of shareholders with tablets are possible are N-1. Let's sort through these N-1 states. During this time, all N shareholders must "go" for their own signs. According to the Dirichlet principle , at least one of the enumerated N-1 states must have at least two of N comparisons. In other words, there is a state in which at least two shareholders are sitting at their own signs. CTD.
- N sages lined up "train", each put on a cap of white or black. Each sage hears what is said around him and sees the colors of the caps in front of the wise men standing, but he does not see his cap and the caps of the wise men standing behind. All of them in turn, starting with the last one, are asked the question: “What color is your cap on?”. A sage is allowed to answer only "white" or "black." Develop an algorithm for the actions of the sages so that the number of correct answers is not less than N-1.DecisionDenote the white cap unit, black cap zero. The last sage adds the colors of the caps in front of the standing sages modulo 2 (x them). Calls the color corresponding to the resulting amount. The further fate of the last sage is not so interesting: perhaps the named color coincided with the color of its cap, perhaps not. The next sage, having calculated the sum of the caps in front of him, adds it to the color called the last sage, and receives the color of his cap, which he calls. The next one adds three numbers already: the number of white caps standing in front and the numbers said by the two previous sages. Subsequent sages operate in the same way. It turns out at least N-1 correct answers.

Please report in the comments on alternative ways of performing tasks, including more complex or unsuccessful ones, as well as any errors and typos.
Enjoy your decision!
UPD . makaroni4 created a test of some tasks. Thank!
Source: https://habr.com/ru/post/228489/
All Articles