Experiments with bit-reverse patterns in two-dimensional additive cellular automata

Somehow I experimented with cellular automata. With one-dimensional and two-dimensional. Invented on what the initial state to apply a rule. When, as the initial state of a two-dimensional cellular automaton, I began to use a bit-reversible permutation of the diagonal line, then after the application of the automaton, original patterns were obtained. From time to time, distinct patterns appeared among the patterns. I selected these patterns and experimented with them a little. With what I managed to find out, I am sharing in this article.

In the article I will briefly tell you about additive cellular automata. And also I will give a sequence of my observations and tasks that I set. Each stage will be accompanied by images of the state of the cellular automaton. In addition, for better visibility, I wrote a web application that will add interactivity when reading an article. The application is based on React and should work in modern browsers. Also I will accompany some actions with links with pieces of Python code.

Disclaimer: The article is purely informational and entertaining, because I do not know the applications of the proposed information. Also, it is interesting to me to organize the fragmentary information that I managed to find out. And, perhaps, to find in them roughness. Perhaps new experiments will come to my mind.
')
I hope that the article will entertain you, although I will write clearly and to the point.

Preliminary acquaintance with cellular automata

If you are not familiar with cellular automata (CA) or just heard about them, then I suggest reading the introductory articles:

Tofholi T., Margolus N., A Review of Cellular Automata ( pdf ) on The Game of Life by Roman Parpalak is a good introduction to the SC.

Evgeny Zolotov, World in the box ( pdf ) on Computerra.

More practical articles:

OCo, Cellular Automata ( pdf ) for Programs, fractals and all sorts of things from OCo - a brief introduction to cellular automata and examples of the implementation of various cellular automata.

Matvey Kotov ( mkot ), A little bit about cellular automata on Habré.

Tatyana Bibikova, Hydrodynamics of the sea urchin spermatozoon ( pdf ) - the story of the scientific work.

I will also cite, in my opinion, materials in English:

Elementary Cellular Automaton on WolframMathWorld - the approach of numbering the rules of spacecraft is described and illustrations of the behavior of all rules are given for a certain starting state.

Elementary cellular automaton on Wikipedia is about the same as the previous one. But there are illustrations of the application of some rules in a random starting state.
Rafael Espericueta, Cellular Automata Dynamics ( pdf ) is an illustrated book about zero-dimensional, one-dimensional and two-dimensional spacecraft.
Additive Cellular Automaton on WolframMathWorld - about additive spacecraft.

Mirek Wojtowicz, 1D and 2D Cellular Automata explorer - the site has a collection of CA rules.

2D Additive Cellular Automaton

A cellular automaton has a state and a rule according to which the transition from the previous state to the next one occurs.

The state of a two-dimensional spacecraft is a two-dimensional array of cells. In our case, this array has the same length and width N. Each cell can take values 0 or 1. We will depict cells with value 0 in black, and cells with value 1 in white.

The position of the cell in the state array of the spacecraft is described by the coordinates [i, j], where i, j take values from 0 to N-1, moreover, i is the column number, and j is the row number.

A rule is a procedure that, based on the value of the cell and the value of the neighboring eight cells, calculates the value of the cell for the next state. The set of cells that can participate in the calculation of the rule will be called a neighborhood. This is the neighborhood of the cell [i, j]:

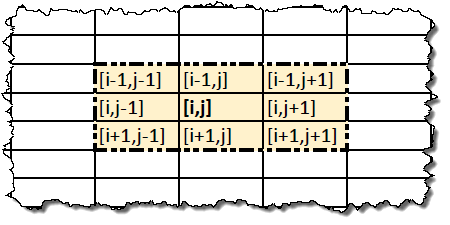
The rule calculation procedure is applied in parallel and equally for all cells of the state of the AC, in which all neighboring cells are defined (in a typical implementation - sequentially using two state arrays.) A single application of the rule to all cells will be called one iteration.

At the boundaries of the state of the spacecraft, not all neighboring cells are defined. There are various ways to identify missing cells. And each method gives a different result. In our case, the missing neighboring cells will be taken from opposite edges of the state. Thus, our array seems to have the left edge with the right edge “glued together”, and the upper edge with the lower edge. Such a "gluing" emulates the surface of a torus, or else it is called a toroidal lattice.

.
Perhaps the most famous example of a two-dimensional spacecraft is the game "Life . "

In a two-dimensional additive cellular automaton (AKA), the procedure for calculating the rule calculates the sum modulo 2 (the same as XOR) of the values of certain cells from nine cells from the neighborhood of the calculated cell. In our case, the value of the cell in the amount is not more than once.

Denote the calculated cell with the coordinates [i, j] as c ₁ , and the neighboring cells as c ₂ , c ₄ , c ₈ , c ₁₆ , c ₃₂ , c ₆₄ , c ₁₂₈ and c ₂₅₆ with the location according to the diagram:

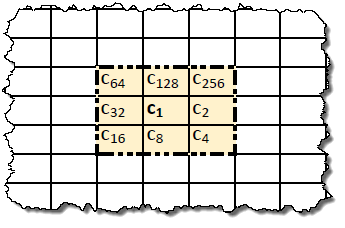
As you have noticed, the indices of the cells in the neighborhood take values of the form 2 ⁿ , where n varies from 1 to 9. Such indices are very convenient, since the sum of arbitrary indices gives a number that in binary representation uniquely determines which cells are included in the sum for calculating the rule. This number will be the rule number.

For example, rule 15 . According to the binary representation 15 = 000001111 ₂ , it is decomposed into the terms 000000001 ₂ , 000000010 ₂ , 000000100 ₂ , 000001000 ₂ or 1, 2, 4 and 8. Hence, rule 15 means that each cell of the new state is the sum of cells with ₁ , s ₂ , ₄ and _{8 of the} previous state. Other adjacent cells are not involved in the rule calculation. Thus, the rule calculation procedure is an expression with ₁ [t] = with ₁ [t-1] + with ₂ [t-1] + with ₄ [t-1] + with ₈ [t-1] (mod 2), where c ₁ [t] is the cell of the new state, and c ₁ [t-1], c ₂ [t-1], c ₄ [t-1], c ₈ [t-1] are the cells of the previous state, and the coordinates cells with ₁ [t] and with ₁ [t-1] match, and cells with ₂ [t-1], with ₄ [t-1], with ₈ [t-1] are adjacent cells with cells ₁ [t- 1] according to the chart.

The idea of this numbering of the rules of the AKA is taken from [ Khan1997 ].

In the application, you can interactively set a rule, either by number or by ticking checkboxes with cells in the neighborhood. If you change one view, the other view will change automatically.

All the material of the article is based on the use of rule 15. Also, there will be a couple of experiments using rule 511 .

Preliminary identification of diagonal line permutation

Take the empty state of AKA 64x64 cells, and draw a diagonal line :

.
Apply a bit-reversible row permutation. Or columns. No difference. What is the reverse of bits and bit-reverse permutation I already wrote. [ BRH2012 ] In the application, this is done with the BRP (y) button or by selecting Pattern “Permuted Diagonal Line”. Get the state :

.

Now we will iteratively apply rule 15 to this state (the “Apply rule” button.) After 30 iterations, we get the state:

.
My eye is already swept up, and I easily recognize the desired patterns. From this state, one can distinguish something that has the size of 8x8 consisting of virtual black and white cells, repeated four times with various drawing methods. Highlight this explicitly:

.
It would seem that a set of cells. After all, each iteration gives a certain pattern. Why did I select this particular iteration and this drawing?

Let's take AKA 128x128 cells . And do the same. Let us dwell on iteration 62. We see the state:

Experiment without comment

Press the BRP (x, y) and 4BRP (x, y) permutation buttons in different sequences. Similar permutations can be achieved with the PG (x, y) button. Thus, it is possible to obtain a pattern in its pure form without recognition of virtual cells.

We see virtual cells that define a 16x16 pattern. Select it:

.

To finally make sure, take an AKA 256x256 cell . Here is the state at iteration 60:

.
We see virtual cells defining the familiar pattern of 8x8 cells. Only the way of drawing virtual cells differs. In the following iterations, the pattern is repeated in one or another way of drawing. For example, iteration 62:

.
Finally, iteration 126:

.
Recognizable picture, is not it? Also, pay attention to the dynamic moire pattern with the smooth movement of this pattern on your LCD monitor. But this is a topic for another article. Let's select the pattern 32x32 from virtual cells:

.

This was enough for me to embrace an interest in this object and explore it more deeply. Let us call this object the manifestation of a permutation of a diagonal line or PPDL.

I decided to figure out how to generate such patterns in their pure form without doing many iterations of the AKA and not recognizing virtual cells.

Generation of diagonal line permutation manifestation

Take the PITP in its pure form 32x32 cells . Apply rule 15 to it (from the very beginning, I experimented only with rule 225 , which led to the appearance of unnecessary corrections when generating the PFMD.) We get the state:

.
If you tinker a bit with this state, then you can come to the conclusion that in each quarter there is a bit-reversible permutation of the diagonal line. Check this by pressing the 4BRP (y) button. We get:

.
Also, you can not rearrange each quarter separately, and rearrange the status bar entirely . Then get two diagonal lines . It would seem that there is no difference what approach to choose. But, in the transition to an arbitrary module / base, with the first option, the generation is easier. (From the very beginning, in my experiments, I used the second method. And I finally came to the first method right at the time of writing the article.)

And so, we know the state of the AKA after applying the rule 15. And such a state is easy to generate for a given size.

It remains to reverse this state. Let's write out rule 15 again:
₁ [t] = ₁ [t-1] + ₂ [t-1] + ₄ [t-1] + ₈ [t-1] (mod 2), where ₁ [t] is known the cell of the state containing permutations of the diagonal lines in each quarter, and c ₁ [t-1], c ₂ [t-1], c ₄ [t-1], c ₈ [t-1] are unknown PPDL cells. If you look at the detected PPDL of various sizes, it is easy to see that the cells of the first row and the first column contain only zeros. Thus, we will assume that we already know the meaning of the first ppl cells. Based on these values, it becomes possible to find the rest of the values of the PDDL cells.

For example, take AKA 8x8 cells. The state t with permutations of the diagonal lines in each quarter is depicted as a table:

Let us display in the form of a table the desired state of the PDLS t-1 with the known first row and first column:

Three known cells in the upper left corner will correspond to the following rule 15: ₁ [t-1], ₂ [t-1], ₈ [t-1]. Unknown cell [1,1] corresponds to the addendum with ₄ [t-1]:

.

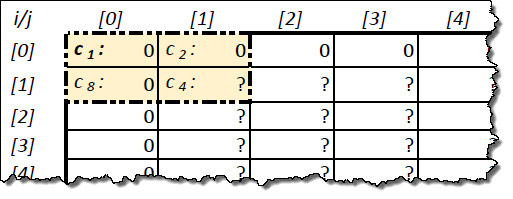Other terms in rule 15 are not involved.

Solve the equation for c ₄ [t-1]. We get:
c ₄ [t-1] = c ₁ [t] + c ₁ [t-1] + c ₂ [t-1] + c ₈ [t-1] (mod 2) (when adding modulo 2, the minus sign does not matters.) According to the tables, with ₄ [t-1] = 1 + 0 + 0 + 0 = 1 (mod 2). Get the state:

Similarly, a cell [1, 2] or a cell [2, 1] is calculated taking into account the displacement:

.
Etc. Cell by cell, line by line , we get the state:

* * *

Also, PPDL can be generated using block-recursive matrix construction . If it is interesting to someone, you can try to do it yourself.

Some properties of the manifestation of the permutation of the diagonal line

Property 1

PPDL has a size N equal to the power of two, i.e. N = 2 ⁿ .

Property 2

The cells of the first row and first column are zero.

Property 3

Even cells on row N / 2 and column N / 2 are equal to one, and odd cells are equal to zero. In other words, they are equal to the corresponding cell coordinate, taken modulo 2.

Property 4

If rule 15 is applied to the PSDP, then we obtain a state that contains permutations of the diagonal line in each quarter.

Property 5

Prepare a pdl 64x64 cells :

.
And we will apply rule 511. At iteration 16 we get:

.
This is the same pattern, only shifted by 32 cells diagonally.

A similar picture occurs with PPDL of other sizes.

The pattern obtained in this way can be generated as well as the main one, only you need to take the first row and the first column, which consist of units on even cells .

It should be noted that this is not a unique property of this pattern. You can think of other AKA states that have the same property.

If you continue to apply the rules 511, then at iteration 32 the original image will be returned. The original image is restored with any combination of AKA state cells, but not with any size of state. This property rules 511 propose to apply in cryptography. [ Chatz2012 ] From this source, I learned about the possibility of using rule 511 in my experiments.

* * *

Exploring other areas, I was faced with the fact that if there are objects in which calculations with module 2 are applied, then they can be extended to an arbitrary module> = 2.

The manifestation of the permutation of the diagonal line with an arbitrary module / base

First, we expand the rule calculation procedure. Now, the rule calculation will calculate the sum of the selected cells of the neighborhood taken modulo M> = 2. That is, after we calculate the sum of the values of the selected cells, we will take the remainder of the division by the number M as the final value of the cell. Thanks to the calculation modulo M, the cells of the AKA state will take integer values from 0 to M-1.

Cells with a value of 0 will be displayed in black, cells with a value of M-1 will be depicted in white, and intermediate values of cells will be depicted as intermediate shades of gray.

Something about AKA with a module> = 2 is in [ CAD1997 ].

Also, it is necessary to move from the reverse of bits, which is the reverse of digits with base 2, to the reverse of digits with arbitrary base B> = 2. Reversing the numbers will allow you to make a digital-reverse permutation of the diagonal line (I'm not quite sure that I entered the terms correctly. I thought about the options: reverse numbers / digits and digital-reverse permutation. But, in my opinion, it looks terrible.) It would also be incorrect if the size of the state of the ATM will be a degree 2. You need to adjust the size of the state of the AKA. Now this size N will be some degree of base B, i.e. will have the form N = B ⁿ .

Let's experiment with rule 15. The module and the base must match. Times Two .
In the second case, at iteration 62, something remotely similar appeared:

.
There are virtual cells, but all this is not that.

Stumbled in while writing an article ...

At iteration 125, the following state appears:

If we apply the permutation PG (x, y) three times, then we get fragments with the desired pattern:

Then I tried rule 511 . Take the permutation of the diagonal line with a module / base 3 and size 243x243. At iteration 26 we get:

.
Clearly visible virtual cells 5x5 (correct 6x6), and recognizable pattern:

.
Take the permutation of the diagonal line with module / base 3 and size 729x729 . At iteration 80 we get a virtual pattern of size 18x18 .

Similar results can be obtained if we take the permutation of the diagonal line with the module / base 4. But for this you have to calculate the rule with a 4x4 neighborhood , which is not implemented in the application. I can only show the finished results. At iteration 42 we get a virtual pattern of size 8x8 .

We will try to find a way to generate PPDL as we did before.

Take a pdl 18x18 cells with module / base 3:

.
Apply rule 15 and get terrible porridge:

.
Start over. Apply rule 511 :

.
Already better. But still a lot of excess. And no desire to reverse the state according to rule 511.

After a while, I had the idea to experiment with the signs of the components of the AKA rule. In order to designate which addends are applied with a minus sign, I suggest to write another number after the rule number, which uses the same coding as the rule.

For example, rule 15-10. It includes the terms c ₁ , c ₂ , c ₄ , c ₈ . But the terms c ₂ and c ₈ come in with a minus sign. We obtain the function with ₁ [t] = with ₁ [t-1] -c ₂ [t-1] + with ₄ [t-1] -c ₈ [t-1] (mod M)

Rule 15-5 gives the state:

.
And rule 15-10 gives the state:

.
Let us dwell on rule 15-10. Since in the left upper quarter of the cell contain units (gray cells.) Whereas after rule 15-5 - two (white cells.) And one is closer to the beginning of the numerical axis.

Apply the digital-reverse reversal of the rows in each quarter of the last state by pressing the 4DRP (y) button and get:

.
The state can be divided into quarters, and in each of them is a diagonal line with a corresponding value.

And so, we became aware of the condition that needs to be obtained after applying rule 15-10. It remains to reverse this state. Let's write out rule 15-10:
c ₁ [t] = c ₁ [t-1] -c ₂ [t-1] + c ₄ [t-1] -c ₈ [t-1] (mod M), where c ₁ [t] is known the cell of the state containing permutations of the diagonal lines in each quarter with the corresponding value, and c ₁ [t-1], c ₂ [t-1], c ₄ [t-1], c ₈ [t-1] - unknown PPDL cells , M - module (at the moment it is equal to 3.) Fix the values with ₁ [t-1], with ₂ [t-1], with ₈ [t-1] as we did before. Solve the equation for c ₄ [t-1]. We get:
c ₄ [t-1] = c ₁ [t] -c ₁ [t-1] + c ₂ [t-1] + c ₈ [t-1] (mod M). Having calculated all the unknown cells we get the desired pattern.

Thus, obtaining patterns with a module / base M> = 2 is similar. It is necessary to take a state, a quarter of which has a size, as a degree of foundation Draw diagonal lines with a digital-reversal permutation in each quarter.In the upper left and lower right quarters, cells take the value 1. And the other two quarters take the value M-1. Then reverse the resulting state according to rule 15-10. Source Code .

The only thing that confuses is that the pattern was identified using rule 511-0. To make sure that the guesses are correct, let's check rule 15-10 on the rearranged diagonal line . At iteration 52 we get:

.
The picture is identical to that obtained earlier with the help of rule 511-0 with an accuracy of bias.

This bias would not be ...

511. 511 . 15-10, , . , 511 :

, :

Experiments with other sizes of the AKA state using rule 15-10 give patterns with virtual cells that coincide with the PDL that is generated by the above algorithm.

* * *

I also managed to implement the generation of PDL with base / module 3 using block-recursive matrix construction. Investigating the block structure of the PSDL, I noticed that the structure of the blocks becomes more and more complex with an increase in the module / base. An element similar to the matrix of the discrete Fourier transform (ie, the matrix in the form of a multiplication table modulo) is also becoming noticeable. But I don’t want to overload this article with a detailed study in this direction. Maybe someone will be more interesting to learn it yourself.

* * *
Let's reconsider the properties of the psdl.