Solving a linear regression problem using the fast Hough transform

Introduction

Friends, let us now consider the linear regression problem in the presence of outgoing (uncorrelated with signal) noise. This task often arises during image processing (for example, with color segmentation [1]), including acoustic [2]. In cases where the coordinates of random variables can be roughly sampled, and the dimension of the problem is low (2-3), in addition to the standard methods of robust regression, you can use the fast Hough transform (BPC) [3]. Let us try to compare this last method in accuracy and stability with the "classical" ones.

Use BPH for linear regression

The problem of linear regression on the plane is to restore a linear relationship between two variables, specified as a set of pairs (x, y). Given a certain level of discretization of coordinates, you can display this set on a single-bit or integer image (in the first case, we note only the fact that there is a point in the source data with approximately such coordinates, in the second one also their number). In fact, we are talking about a two-dimensional histogram of the original data. Thus, informally, the task can be reduced to a search on the image of a straight line that best describes the depicted distribution of points. In such cases, the Hough transform is used in image processing.

The Hough transform is a discrete analogue of the Radon transform and associates each line on the image with the sum of the brightness of the pixels along it (that is, it simultaneously calculates all possible sums along the discrete lines). You can enter a reasonable discretization of straight lines by shifts and tilts so that parallel discrete straight lines tightly pack the plane, and the straight lines emerging from one point at one edge of the image diverge at a slope at the opposite edge by an integer number of pixels. Then such discrete lines on the square n ² will be approximately 4 * n ² . For this discretization, there is an algorithm for quickly calculating the Hough transform with the assymptotic behavior of O (n ² * log n). This algorithm is a close analogue of the fast Fourier transform algorithm, it is well parallelized and does not require any operations other than addition. In [3] one can read a little more about this, moreover, it explains why the Hough transform from an image smoothed by a Gaussian filter can generally be used in a linear regression problem. Here we will demonstrate the stability of this method.

Test data

Let us now ask what distribution we expect from the input data. In the problem of acoustic location, we can assume that we have uniformly distributed points along the straight-line segment of the trajectory of the vessel, distorted by normal additive coordinate noise. In the case of the analysis of color clusters, the distribution along the segment is unknown and often quite bizarre. For simplicity, we will consider only the two-dimensional Gaussian distribution with a high eccentricity. With a sufficiently large dispersion along a straight line and a small dispersion in the transverse direction, the properties of the constructed distribution do not differ much from the “noisy segment”.
')
The algorithm for generating test distributions can be described by the following three steps:

• “center” and slope are randomly selected (a straight line is modeled);
• Generates a specified number of points with the specified distribution (and selected center);
• homogeneous discharge noise is added.

The standard deviation of the normal distribution along a straight line was one-fourth the length of the simulated segment (with this choice, approximately 95% of the points fall inside), and the length of the segment was taken equal to half the linear size of the square image (constituting 512 pixels). The ratio of the variances was 10.0, and the number of distribution points and the proportion of outlier noise varied. An example of this kind of distribution is shown in Figure 1.

In order to compare different algorithms, one must be able to evaluate how well a segment was found in each case. The subtlety is that the algorithms in question are not looking for a segment, but for a straight line. Therefore, we will take the “ideal” segment (A, B) and find the maximum of two distances from its ends to the experimentally found straight line. If we denote by Q (L, AB) the error in the parameters of the experimental straight line L, then this definition can be written as: Q (L, AB) = max (r (L, A), r (L, B)).

Fig. 1. Sample distribution with additive and outgoing noise. The marks indicate the ends and center of the simulated segment.

The dependence of the error of the BPH method on the size of the smoothing window

As mentioned above, regression using BPH involves smoothing. Obviously, the size of the smoothing window should have a significant impact on the quality of the algorithm. We investigate the dependence of the error of finding a straight line on the size of the window. For each size from a set, a series of one hundred images was generated, then a straight line was calculated for each one and an error was fixed. The result obtained is shown in Fig. 2, where the abscissa axis specifies the ratio of the smoothing parameter s _H to the standard deviation of the normal ("transverse") component of the coordinate noise s _L. The dots in the figure denote the average errors, and the standard deviations are laid up and down from them. It can be noted that the result is the best in the case when s _{H is} close to s _L , i.e. when the window size is not much different from the “thickness” of the segment.

Fig. 2. Dependence of the error of the Hough method on the size of the smoothing window.

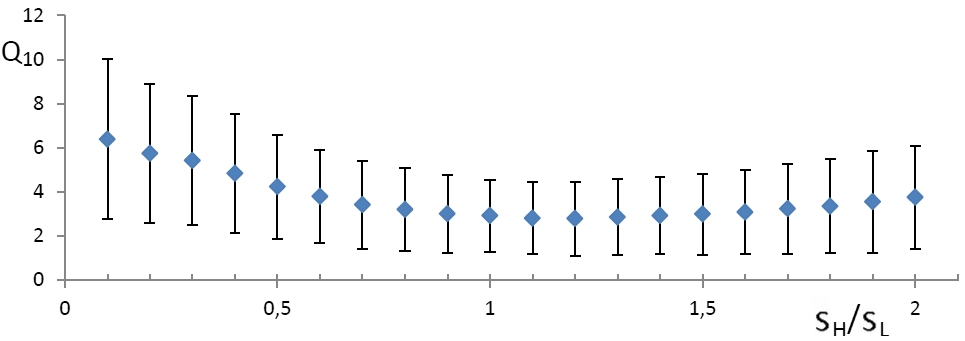Comparison with OLS and its robust modifications

The most obvious, though incorrect (in our case) linear regression method is, of course, the least squares method (OLS), which for orthogonal regression coincides with the principal component method (PCA). At one time, for the case of outlier noise, he was doped to “MNC with iterative recalculation of weights,” and all textbooks include variants with a Huber weight function and a biquadratic weight function [4].

Let's compare the BPH method with a simple OLS, as well as with OLS with recalculation of weights with both weight functions. We take the parameters of functions, as recommended by the theorists: k _H = 1.345 for Huber and k _B = 4.685 for the biquadratic function.

Figure 3 shows how the average error of each of the four methods depends on the density of outlier noise µ - the ratio of the number of outbound noise points to the total number of pixels in the image (the density of outlier noise is plotted on the x-axis, and the average method error is shown on the ordinate axis). Each measurement was carried out on a hundred different generated images. From the figure it is obvious that the method based on the application of BPH turned out to be the most resistant to adding outlier noise, although with a small number of outliers it is inferior to other methods in accuracy. In addition, this method turns out to be more stable, that is, it is less often mistaken catastrophically (a quarter of the standard deviation of the error is postponed up and down from each point in the figure).

Fig. 3. Dependence of the average error on the density of emissions of noise in BPC and OLS methods.

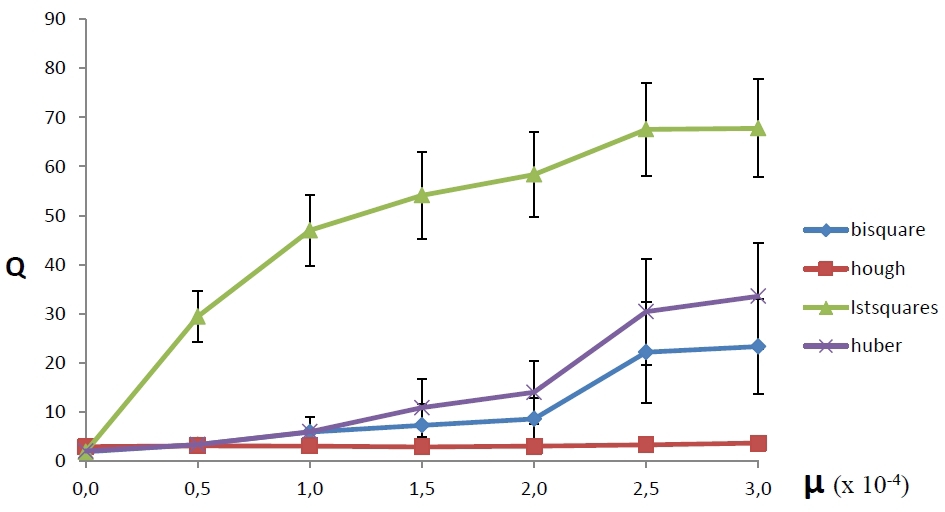Comparison with median methods

Surprisingly, the really good methods of robust regression are rarely talked about in universities. But we, dear reader, know about the magic method of Theil-Sen [5], and therefore it would be dishonorable to restrict ourselves to a comparison with the robust OLS. In the classical Theil-Sen algorithm, the slope of a straight line is calculated as the median among the slopes of straight lines drawn through all the pairs of sample points. In addition, a modified version is used in which the median of the slopes of all lines passing through this and some other distribution point was selected first for each distribution point, after which the median (“median median”) was selected from the obtained values. In both cases, to determine the straight shift parameter, the median is taken among the values ​​{y _i - mx _i }, where m is the slope of the straight line found by the methods described.

Figure 4 shows the comparison now with these methods. Within each series, one hundred experiments were still carried out, the designations also did not change. It can be seen that in the considered interval of the emission of noise, the average error of the BPC method is the smallest and does not grow, while the Theil-Cen methods have a proportional increase in the error. You can also see that the BPH method still has the smallest error spread.

Fig. 4. Dependence of the average error on the density of emissions of noise in the BPH and median methods.

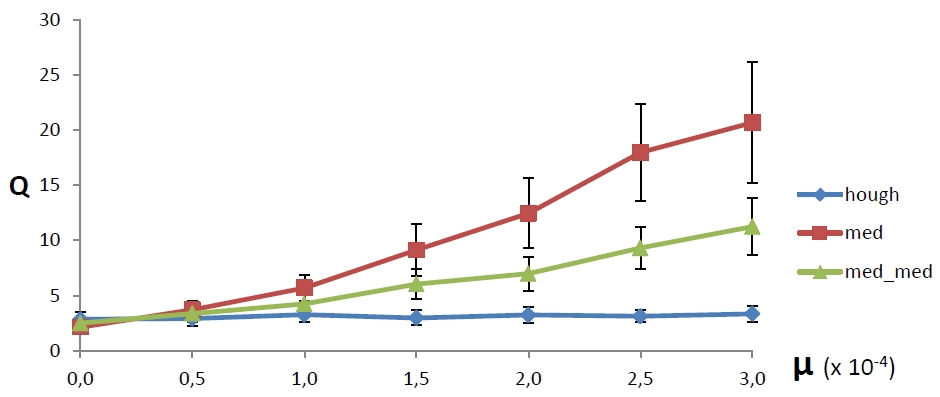Comparison of methods in the presence of structured noise

Of particular interest is the case when outlier noise has its own spatial structure. For example, add to the already considered types of noise uncorrelated with the signal noise component with a circular two-dimensional normal distribution. An example of a combination of all three types of noise is shown in Figure 5. The straight line shows the perfect answer.

Fig. 5. An example of a segment, noisy additive, as well as uniform and structured emission noise.

Let us now look at the dependence of the error on the density of “round” structured noise with fixed parameters of outlier and additive noise. Still for each value of the density generated a hundred images. The results are shown in Figure 6. It is noticeable that the methods were divided into three groups, and surprisingly the classical robust methods differ little from the OLS. It can be seen that all OLS-methods “break down” almost immediately, the median methods work stably with much larger data contamination, but also sooner or later stop working, while the BPH method does not have a sharp breakdown at all.

Fig. 6. Dependence of the average error on the density of structured noise.

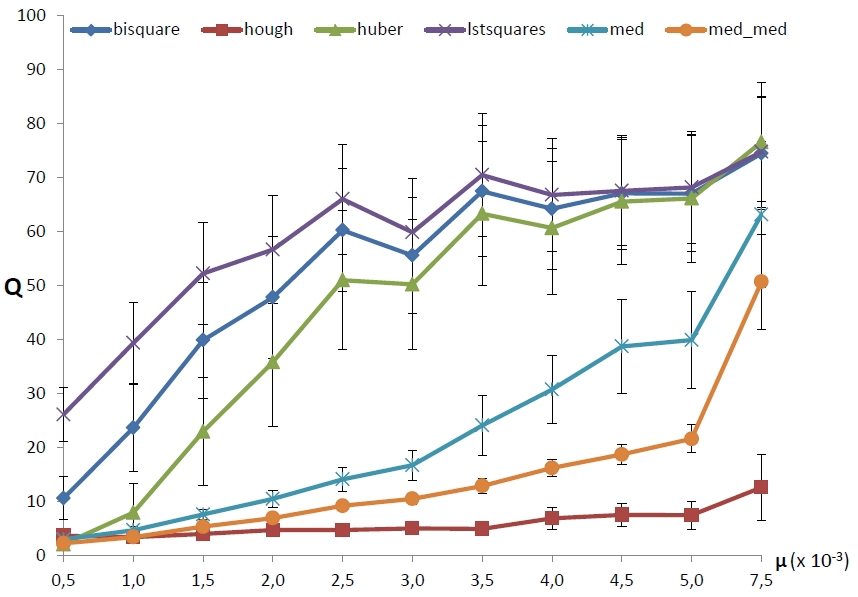Discussion

Solving the linear regression problem using a combination of Gaussian smoothing and Hough transform is resistant to the additive coordinate and emission noise that are simultaneously present. Comparison with other common robust methods showed that the proposed algorithm is more stable when the emission noise density is high enough. It should be noted, however, that the method is applicable only in the low-dimensional case (the BPC algorithm can be generalized to any dimension, but the amount of memory required for encoding a task as an image of a dimension higher than three is frightening). In addition, even in the two-dimensional case, the use of BPH will be disadvantageous if the points are small and the required relative coordinate accuracy is high. This is due to the fact that for the rest of the methods the computational complexity depends on the number of points, and for the BPC - on the number of discrete spaces. However, with a small number of points it is possible to calculate the Hough transform by “brute force”. It would seem that this will not work, because we want to smooth out the image beforehand, however, even Israel Moiseevich Gelfand knew that Gaussian smoothing is in a certain sense commuting with the Radon transform. Using this trick, the assymptotic method in the approximation of a small number of points can be improved to O (n ² ), however, n still denotes the linear size of the image, so it is almost certainly still too bad. But with a large number of points the BPH method covers all other methods like a bull - a sheep. So it goes.

Literature

[1] DP Nikolaev, PP Vision and Image Understanding. 2004, V.94 (Special issue for color indexing and retrieval), pp. 115-139
[2] L. Nolle. Application of computational intelligence for target tracking. In Proc. of 21st European Conference on Modeling and Simulation, 2007, pp. 289-293.
[3] DP Nikolaev, SM Karpenko, IP Nikolaev, PP Nikolaev. Hough transform: Underestimated Tool in Computer Vision Field. In Proc. of 22nd European Conference on Modeling and Simulation, 2008, pp. 238-243.
[4] PJ Rousseeuw, AM Leroy. Robust Regression and Outlier Detection. Wiley series in probability and statistics, 2003.
[5] Wilcox, R. Rand. Theil – Sen Estimator, Introduction to Robust Estimation and Hypothesis Testing, Academic Press, 2005, pp. 423–427.