How to win in the game stone-paper-scissors? (implementation of the optimal strategy in Wolfram Mathematica)

Translation of the post of John McLune (Jon Mcloone, Director of International Business and Strategic Development, Wolfram Research). Original post: How to Win at Rock-Paper-Scissors

Download the post in the form of a document Mathematica



From the point of view of mathematics, the rock-paper-scissors game (see Appendix 1 at the end) is not particularly interesting. The Nash equilibrium strategy is very simple: randomly and with equal probability choose from three options, and provided you have a large number of games, neither you nor your opponent can win. Although, when computing a strategy using a computer, it is still possible to win a person after a large number of games.



My nine-year-old daughter showed me a program that she created with Scratch, which won absolutely every time just by tracking what choices you made before you made yours! But I will introduce you to a simple solution that wins a man in stone-scissors-paper without cheating.

')





Since the one who always makes an absolutely random choice cannot be defeated, we will rely on the fact that people are not very random. If the computer can notice a certain pattern in which you act in your attempts to be random, it will be one step closer to predicting your future actions.



I thought about creating an algorithm as one of the topics of our course of statistics in the framework of the concept of Computer-Based Math . But the very first article I stumbled upon in search of predictive algorithms considered the solution using a complex construction based on copula-distributions. This decision was difficult for the student to understand (and perhaps for me), so I decided to develop a simpler solution, which I could explain in simple words. And even if it was already developed earlier, it is much more fun to create things in your own way than to find their ready implementation.



To start, we just need to be able to start the game. At that time, a demonstration was already developed and available that allows you to play stone-scissors-paper, but this was not exactly what I needed, so I wrote my version. This item does not require special explanation:



In [1]: =







Out [1] =







For the most part, this code describes the user interface and the rules of the game. The whole strategy of a computer player is contained in this function:



In [2]: =







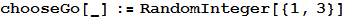
where 1 corresponds to stone, 2 to paper and 3 to scissors. This is the best solution. No matter how you play, you will win as many games as the computer, and your victory rate will fluctuate around zero.



So, now it would be interesting to rewrite the function chooseGo to predict your choice using the latest games data stored in the history variable. The first step will be an analysis of the choices made during the last few games and the search for all occurrences of any sequence. Watching what a person did in each next game, we can find a certain pattern of behavior.



In [3]: =







The first argument of the function is the history of past games. For example, in the data set below, a computer (the second column is the second element of each sublist) just played a paper (it corresponds to number 2) against a stone played by a person (number 1). This is evident in the last element of the list. It is also clear that this situation has already arisen twice, and both times the next move of the person was again a stone.



In [4]: ​​=







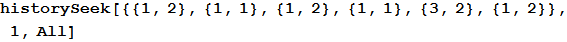
Out [4] =







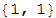
The second argument is the number of the last elements of the story that will be searched. In this case, the number 1 is passed as the function argument, which searches only the occurrence cases {1,2} in the data. If we select 2, the function will search for occurrences of the sequence {3,2}, {1,2} and return an empty list, since such a sequence has not previously been encountered.



The third argument, All , indicates that the sequences of the person and the computer must match in the desired sequences. The argument can be changed to 1 to look only at the history of a person’s moves (that is, assuming that human choice depends only on his previous moves), or 2, to pay attention only to the second column, that is, the history of computer moves (that is, assuming that the person responds to previous moves of the computer, regardless of which moves he made and, therefore, regardless of whether he won or lost).



For example, in this case we find that a person chose after a stone, regardless of the fact that in the same games he chose a computer.



In [5]: =







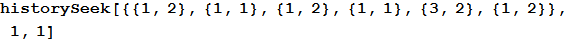
Out [5] =







Having a large amount of data, we can only manage with the argument All , and the program can decide for itself whose moves, computer or person, are more important. For example, if a computer’s move history is ignored by a person during a selection, then the data set obtained for a computer’s move history will have the same distribution as any other computer’s move history, provided that there is enough data about previous games. When searching through all pairs of games, we get the same result as if we first selected data on the history of computer moves, and then used this subset for the function shown above. The same will happen if only the history of the moves of the computer is important. But at the same time, performing a search when taking into account both of these assumptions separately can get more true matches in history, and most of all this is manifested in cases where the set of data about the games is initially small.



Thus, from these two checks we can find that the first one gives a 100% estimate, that the next choice of a person will be a stone, and the second shows that with 75% probability a person will choose a stone and with a 25% probability - scissors.



And here I am somewhat stalled in solving the problem.



In this case, the two predictions are at least more or less similar in result, although they differ in numerical values ​​of probabilities. But if you conduct a search on three “slices” of data with a number of different lengths of history, and the results of the predictions are contradictory - how to combine them?



I put a note about this issue in the “Write about it to the blog” folder and forgot about it until a few weeks ago there was a dispute about how to highlight the concept of “ statistical significance ” in the course of Computer-Based Math.



I realized that the question is not how to combine the obtained predictions, but how to determine which of the predictions is the most significant. One of the predictions could have been more significant than the others, since it reflects a more pronounced tendency or, perhaps, is based on a larger set of data. It was unimportant for me, and therefore I simply used the p-value of the significance test (with the null hypothesis that both players play randomly) in order to streamline the predictions.



I think I should listen to our first principle that the first step in solving any mathematical problem is “the right question”.



In [6]: =







Now, if we take the last result we obtained, it turns out that the best prediction is a stone with a p-value of 0.17. This means that only with a probability of 0.17, the data used for this prediction deviate from the discrete uniform distribution ( DiscreteUniformDistribution [{1,3}] ), and more so by chance rather than due to a systematic error produced by a human or another reason that could change the distribution.



In [7]: =







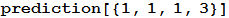
Out [7] =







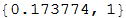
The smaller this p-value, the more confident we can be that we have found a real pattern of behavior. So we just carry out the predictions for different history lengths and data slices and choose the prediction with the lowest p-value.



In [8]: =







And we make a choice that will beat the choice of a person.



In [10]: =







Here you see the result. You can download and test it yourself from the Wolfram Demonstrations website.



In [11]: =







Out [11] =







When a program has too little data, it plays randomly, so you start on an equal footing. At first, when she begins to learn, she makes some stupid decisions, so you can get ahead. But after 30-40 games, it starts to receive really meaningful predictions, and you will see how your victory rate drops to a negative area, and so it will remain there.



Of course, such a decision is good only against primitive attempts to appear random. Its predictability makes it susceptible to possible loss against a well-calculated and intended strategy. It is extremely interesting to try to defeat this program with the help of intuition. This is possible, but if you stop thinking or you think too hard, you will soon be left behind. Of course, the program could easily do this by applying the same algorithm to predict the next move of this program.



Such an approach leads to the beginning of a certain “arms race”, a competition in writing algorithms that will win in a stone-scissors-paper from a rival algorithm, and the only way to stop it is to return to the Nash equilibrium strategy, choosing through RandomInteger [{1,3 }] .



Supplement 1

In the event that you do not know how to play this game, the rules are as follows: you choose a stone, scissors or paper using one of the three gestures shown by you and your opponent at the same time. The stone defeats the scissors (makes them dull), the scissors defeats the paper (they cut it), and the paper defeats the stone (it wraps it). The winner gets one point, in case of a draw both players do not get points.



I thank Sergey Shevchuk for the help rendered in the translation of this post.