Implementation of the secret visual information sharing scheme in MATLAB

Introduction

Good day to all!

I am sure that many of you were already interested in the methods of sharing secret visual information. If this is so, then you are certainly familiar with the work of Moni Naor and Adi Shamir on visual cryptography, as well as with the post of April 19, 2013. The scheme of sharing secret visual information . I studied the algorithm and function code written in MATLAB, proposed in this article, and came to the conclusion that it was not rationally written: it can be written much shorter, as well as improve its efficiency. How to do this, I will describe below. Also consider how to organize.

Code optimization

The disadvantage of this function is that the program repeatedly repeats the same type of code, which increases the size of the function, complicates its implementation, while the tools available in MATLAB allow you to write it shorter.

I propose to optimize the getShdwImg function code as follows:
')

function [S1,S2] =getShdwImgrac2x2(Img) %    S1  S2     (Img) % %     [m,n] = size(Img); %       :) S1= zeros(2*m,2*n); S2= zeros(2*m,2*n); r1=[1 0; 1 0]; r2=[0 1; 0 1]; r3=[0 0; 1 1]; r4=[1 1; 0 0]; r5=[1 0; 0 1]; r6=[0 1; 1 0]; r=cat(3, r1, r2, r3, r4, r5, r6); %      -   . 1 % : for i=1:m-1 for j=1:n-1 k = randi(6); if(Img(i,j)==1) S1(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k); S2(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k); else if (mod(k,2) == 0) S1(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k); S2(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k-1); else S1(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k); S2(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k+1); end end end end 

Let us consider in detail what the differences of this code are in comparison with the source code:

• Let's declare a set of variables r1-r6, 2 × 2 in dimension, filled in such a way that the combinations of states of the pixel are given, shown in Figure 1. The function will work with 6 possible combinations, unlike the source code.
  
  
  
  

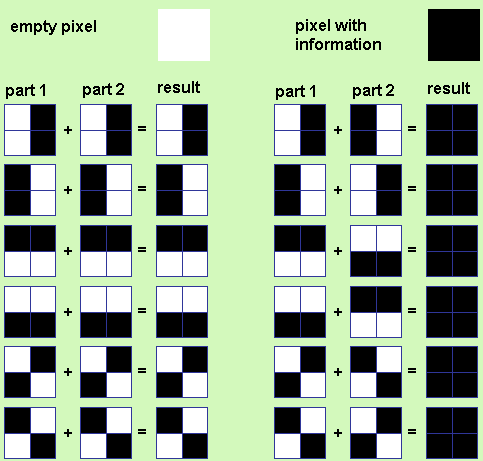
   r1=[1 0; 1 0]; r2=[0 1; 0 1]; r3=[0 0; 1 1]; r4=[1 1; 0 0]; r5=[1 0; 0 1]; r6=[0 1; 1 0]; 

  
  
• The entered variables are combined into a three-dimensional array using the cat command (3, a, b, c ...). The first attribute of the command indicates the dimension of the array into which the arrays listed after the first attribute will be combined.
  
  

   r=cat(3, r1, r2, r3, r4, r5, r6); 

  
  
  
• We connect the operator that generates an integer value of the variable k randomly from 1 to 6.
  

   k = randi(6); 

  
  
  
• Inside the conditional operator, in the case when the condition is satisfied, we write the variables S1, S2. The cells that will be assigned values ​​from the variable r. The value will depend on the randomly generated number k, since we will refer to k to the layer r (:,:, k).
  
  

   S1(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k); S2(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k); 

  
  
  
• If the condition is not fulfilled, then I connect another conditional if statement. His task is to change the index of the layer of the array r, which will be assigned to the variables S1, S2. So if the variable k is even, then the indices will be assigned as follows:
  
  

   S1(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k); S2(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k-1); 

  
  
  Otherwise, the layer index will be determined by the following formula:
  
  

   S1(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k); S2(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k+1); 

  
  
  
• It is not necessary to change the code of the Matlab-script that demonstrates the work of the secret visual information sharing algorithm.
  
  

   close all %   RGB-      biImg = imread('e_30.jpg'); biImg = rgb2gray(biImg); level = graythresh(biImg); %     (Otsu) biImg = im2bw(biImg,level); %     figure(1) imshow(biImg); title(['Original binary image']); %     [S1,S2] =getShdwImgrac2x2(biImg); %     figure(2) imshow(S1); title(['Shadow image S1']); % figure(3) imshow(S2); title(['Shadow image S2']); %          %   figure(4) %imshow(and(S1,S2)); imshow(~xor(S1, S2)); %  “~”(NOT) ,       ,    title(['Superimposed image']); 

  
  
  

Source image


Original image converted to binary


First shadow image


Second shadow image


Image obtained by combining two shadow images using the logical operator ~ xor

And now I bring to your attention the function code for Shamir's secret sharing scheme (3.3) for the binary image.

Development of the function code for the Shamir secret secret separation scheme (3.3) for a binary image

This function is intended for dividing an image into three shadow ones. The original image can be restored only by matching all three shadow images. In general, its code is similar to the code outlined above, but it has a number of significant additions.

 function [S1,S2,S3] =getShdwImgrac3x3opt(Img) %        % S1, S2, S3     (Img) % %     [m,n] = size(Img); %  3        ) S1= zeros(2*m,2*n); S2= zeros(2*m,2*n); S3= zeros(2*m,2*n); %        c01=[0 0 1 1; 0 1 0 1; 0 1 1 0]; c02=[1 0 0 1; 1 0 1 0; 0 0 1 1]; c03=[1 1 0 0; 0 1 0 1; 1 0 0 1]; c04=[0 1 1 0; 1 0 1 0; 1 1 0 0]; c0=cat(3, c01, c02, c03, c04); c05=[1 1 0 0; 1 0 1 0; 1 0 0 1]; c06=[0 1 1 0; 0 1 0 1; 1 1 0 0]; c07=[0 0 1 1; 1 0 1 0; 0 1 1 0]; c08=[1 0 0 1; 0 1 0 1; 0 0 1 1]; c1=cat(3, c05, c06, c07, c08); %       3   %  for i=1:m-1 for j=1:n-1 d=randi(4); %     c k = randperm(3); %   if(Img(i,j)==1) S1(2*i-1:2*i, 2*j-1:2*j)=reshape(c0(k(1),1:4,d), 2, 2); S2(2*i-1:2*i, 2*j-1:2*j)=reshape(c0(k(2),1:4,d), 2, 2); S3(2*i-1:2*i, 2*j-1:2*j)=reshape(c0(k(3),1:4,d), 2, 2); else S1(2*i-1:2*i, 2*j-1:2*j)=reshape(c1(1,1:4, d), 2, 2); S2(2*i-1:2*i, 2*j-1:2*j)=reshape(c1(2,1:4, d), 2, 2); S3(2*i-1:2*i, 2*j-1:2*j)=reshape(c1(3,1:4, d), 2, 2); end end end 

Let us consider in more detail the differences between the getShdwImgrac3x3opt function and the getShdwImgrac2x2 function.

• In the variables m, n, the size of the original image is written, after which three zero matrices with dimensions of 2 * m, 2 * n are created.
  
  

   %     [m,n] = size(Img); %  3        ) S1= zeros(2*m,2*n); S2= zeros(2*m,2*n); S3= zeros(2*m,2*n); 

  
  
  
• Based on the article, Shamir developed 4 arrays of 4 columns and 3 rows for black and white pixels, respectively. Every 4 arrays are combined into the corresponding three-dimensional array of 4 layers.
  
  

   %        c01=[0 0 1 1; 0 1 0 1; 0 1 1 0]; c02=[1 0 0 1; 1 0 1 0; 0 0 1 1]; c03=[1 1 0 0; 0 1 0 1; 1 0 0 1]; c04=[0 1 1 0; 1 0 1 0; 1 1 0 0]; c0=cat(3, c01, c02, c03, c04); c05=[1 1 0 0; 1 0 1 0; 1 0 0 1]; c06=[0 1 1 0; 0 1 0 1; 1 1 0 0]; c07=[0 0 1 1; 1 0 1 0; 0 1 1 0]; c08=[1 0 0 1; 0 1 0 1; 0 0 1 1]; c1=cat(3, c05, c06, c07, c08); 

  
  
  
• Now for each of the pixels of the original image are created arrays of 4 cells according to a specific algorithm. To iterate over the cells of the original image, two cycles are applied, one toggles the cell values ​​vertically, and the second horizontally.
  Inside the loop, an integer pseudo-random number generator is applied, which generates the layer number of the three-dimensional array to which we refer. All sorts of permutations of numbers from 1 to 3 are written to another variable.
  
  

   for i=1:m-1 for j=1:n-1 d=randi(4); %     c k = randperm(3); %   

  
  
  
• By modeling, he established a formula by which it is necessary to refer to the necessary cells of new matrices. Each four cells are assigned corresponding values ​​from the matrices compiled in paragraph 2 of the algorithm. In order to properly assign a value, you must use the reshape command (c0 (k (1), 1: 4, d), 2, 2).
  
  This command allows you to transform an existing matrix into a matrix of a given size. So the first parameter is the name of the matrix that will be transformed, the second and third parameters are the size of the matrix to be obtained. In the parameters of the matrix c0, the variable k (1) is used to select the row. In this case, the line number is selected by performing random permutations, which are performed in paragraph 3. Variable d is responsible for selecting the layer of the three-dimensional matrix. Generated randomly in clause 4.
  
  Depending on the pixel color of the original image, values ​​are assigned either from the matrix c0 or from the matrix c1. The choice of the necessary matrix is ​​carried out by the conditional operator else.
  
  After the conditional statement is completed, it is necessary to register the end end commands.
  
  

   if(Img(i,j)==1) S1(2*i-1:2*i, 2*j-1:2*j)=reshape(c0(k(1),1:4,d), 2, 2); S2(2*i-1:2*i, 2*j-1:2*j)=reshape(c0(k(2),1:4,d), 2, 2); S3(2*i-1:2*i, 2*j-1:2*j)=reshape(c0(k(3),1:4,d), 2, 2); else S1(2*i-1:2*i, 2*j-1:2*j)=reshape(c1(1,1:4, d), 2, 2); S2(2*i-1:2*i, 2*j-1:2*j)=reshape(c1(2,1:4, d), 2, 2); S3(2*i-1:2*i, 2*j-1:2*j)=reshape(c1(3,1:4, d), 2, 2); end end end 

  
  
  
• 
  
  This time, the Matlab script calling the getShdwImgrac3x3opt function has also undergone a minor change.
  
  

   close all %   RGB-      biImg = imread('e_30.jpg'); biImg = rgb2gray(biImg); level = graythresh(biImg); %     (Otsu) biImg = im2bw(biImg,level); %       %   figure(1) imshow(biImg); title([' ']); %       getShdwImgrac3x3opt [S1,S2,S3] =getShdwImgrac3x3opt(biImg); %       figure(2) imshow(S1); title(['   ']); %       figure(3) imshow(S2); title(['   ']); %       figure(4) imshow(S3); title(['  ']); %          %   figure(5) S12=xor(S1, S2); S=imshow(~xor(S12, S3));%  “~”(NOT) ,    , %       title(['  ']); 

  
  
  The main difference of this script from its previous version is that an additional variable S12 is created, into which the overlay matrix of images S1, S2 is written. After that, the variable S is written the result of the imposition of matrices S12, S3, which is the final result.
  
  
• We will use the same source image and divide it into three shadow images.
  
• 
  
  
  
  Shadow images
  
• After overlaying three shadow images, the original image was obtained:
  
  
  

Thanks to everyone who read it. Good luck!