Quaternion Encryption Scheme (QES) on FPGA, XeonPhi, GPU

Hi, Habrahabr!

Quaternion data encryption was performed on FPGA DE5-NET, XeonPhi 7120P, Tesla k20 GPU.
All three have approximately the same peak performance, but there is a difference in power consumption.
')
In order not to pile up an article with unnecessary information, I suggest that you familiarize yourself with a brief information about what a quaternion and rotation matrix are in the corresponding wikipedia articles.

To determine the cryptographic strength of the QES algorithm, I ask you to use search engines for a detailed description of the algorithm, one of the authors of which is Nagase T., and one of the articles, for example, Secure signals using.

How can you encrypt and decrypt data using quaternions? Pretty simple!
To begin with, we take a quaternion: q = w + x * i + y * j + z * k and build on its basis a rotation matrix, which we call, for example, P (q).
Note The picture below is from Wikipedia and the matrix there is named Q.



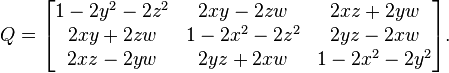
To encrypt data, you must perform the usual multiplication of matrices, for example: B ' = P (q) * B, where B is the data you need to encrypt, P (q) is the rotation matrix, B' is the encrypted data.

To decrypt the data, as you probably already guessed, you need to multiply the "encrypted" matrix B 'by the inverse matrix (P (q)) ^ - 1, so we get the original data: B = (P (q)) ^ - 1 * B ' .

The source data matrices are filled in based on files or, as shown at the beginning, in images.

Below is a variant of OpenCL code for FPGA, the need to transfer the encryption matrix in separate numbers is forced due to the characteristics of the board.

__kernel void quat(__global uchar* arrD, uchar m1x0, uchar m1x1, uchar m1x2, uchar m1x3, uchar m1x4, uchar m1x5, uchar m1x6, uchar m1x7, uchar m1x8) { uchar matrix1[9]; matrix1[0] = m1x0; matrix1[1] = m1x1; matrix1[2] = m1x2; matrix1[3] = m1x3; matrix1[4] = m1x4; matrix1[5] = m1x5; matrix1[6] = m1x6; matrix1[7] = m1x7; matrix1[8] = m1x8; int iGID = 3*get_global_id(0); uchar buf1[3]; uchar buf2[3]; buf2[0] = arrD[iGID]; buf2[1] = arrD[iGID + 1]; buf2[2] = arrD[iGID + 2]; buf1[0] = matrix1[0] * buf2[0] + matrix1[1] * buf2[1] + matrix1[2] * buf2[2]; buf1[1] = matrix1[3] * buf2[0] + matrix1[4] * buf2[1] + matrix1[5] * buf2[2]; buf1[2] = matrix1[6] * buf2[0] + matrix1[7] * buf2[1] + matrix1[8] * buf2[2]; arrD[iGID] = buf1[0]; arrD[iGID+1] = buf1[1]; arrD[iGID+2] = buf1[2]; } 

When using XeonPhi, the results were as follows (Y axis - time, ms; X axis - amount of data, MB):



As can be seen from the graph, XeonPhi responds well to the complexity of the task, that is, when using a conventional desktop processor, the time between 1 and 25 iterations differs approximately 25 times, while here it is approximately two times.
Unfortunately, these results are far from the best, because When programming, OpenMP technology and the possibility of automatic optimization of the Intel compiler were used. When programming at a lower level, i.e. for example intrinsic commands, the results may improve several times.

When using Tesla k20, the results were as follows (Y axis - time, ms; X axis - amount of data, MB):



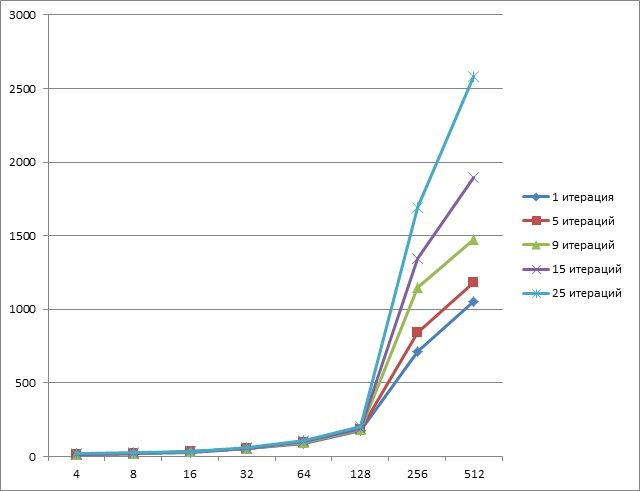
As you can see, pipelining with a small amount of data shows itself perfectly.

When using FPGA De5-Net, the results were as follows (Y axis - time, ms; X axis - amount of data, MB):



At first glance it seems that there is an error in the graphics, but in fact, due to its architecture, FPGA shows an excellent level of pipelining regardless of the size of the data.

Thank you for your attention to this article.

UPD.
Before reading all comments recommend reading
habrahabr.ru/post/226779/#comment_7699309

It will save you some time, thanks.