Waterfall and Agile: and yet, where does the effect come from?
Good day everyone! This short post is devoted to the consideration of models of the development processes of Waterfall and Agile (for example, Scrum and / or Kanban). And here's the thing: from the point of view of the customer, the process is not as important as the time and budget is satisfactory from the point of view of the functional result. And if it is known that (the changes are not taken into account) the costs of the Waterfall process follow the S-curve, and the costs of the Agile process accumulate linearly (since resources are used all at the same time), then how should they differ in efficiency. To explore this question, it is necessary to build models and compare them, and for this, simple mathematics will be used.
Management of the project, conditionally, can be divided into two components - the planning and control of the course.
')
From this point of view, everything is clear for waterfall - we compiled a step-by-step (analytics-development-testing) scheduling of tasks according to estimated deadlines, distributed tasks and implemented them forward.
With Scrum and Kanban it is slightly more difficult: the planning sequence is carried out through priorities in the backlog, development is controlled either through the burndown chart for the entire project (in Scrum), or using the lead time (in Kanban). Estimation of the complexity of the tasks entails an estimate of the dates - through the three iterations or tasks the speed becomes clear, on the basis of which it is possible to estimate the end date.
In this post, the course of the project will not be modeled (this is a completely separate task for itself), and the planned effectiveness will be compared.
Let's present the plan as two components:
Further, we denote as r - the time to implement one unit of task complexity by one specialist, c is the cost of one specialist per time unit, T is the total project time, S is its budget, p = p (t) is the amount of work done at time t .
Then for Agile we have that for a unit of time we will do as much work as N people perform at a time task units:
p ' A (t) = N / r => (knowing that there is no work at first) p A (t) = N * t / r .
Where, in fact, the following is clear:
T A = r * P / N; S A (t) = c * N * t; S A = c * r * P.
At this point, with Agile finished, fortunately, the model of his plan turned out to be (in my version) quite simple. Everything becomes more complicated with the Waterfall-plan, as it involves experts in the course of the project. In this case, however, remains the basic relationship:
p '(t) = n (t) / r .
It's all about the choice of the function n (t) . We know that at zero it is zero, and at the end of the project - zero. We know nothing more. Further, we will assume that it is symmetric, reaches the value of N in the middle, and grows quadratically (I chose the quadratic function from the considerations that this is the simplest variant under the given conditions).
n (t) = N * 4 * (T - t) * t / T 2 .
Knowing that p (0) = 0 , we can write out the integral p '(t) :
p (t) = 2 * N * t ^ 2 / (r * T) - 4 * N * t ^ 3 / (3 * r * T ^ 2) => T = 3 * P * r / (2 * N ) .
ABOUT! But this is already interesting! With the selected law of attracting the team to the project in time, the length of the project grows one and a half times! But the situation with the involvement of not all the staff at once is typical for Waterfall.
What do we have with the cost? It can also be found by integrating (by t ).
s' (t) = c * n (t) => s (t) = 2 * c * N * t ^ 2 * (3 * T - 2 * t) / (3 * T ^ 2) ,
from where
S W = 2 * c * N * T / 3 = c * P * r .
The budget is the same.
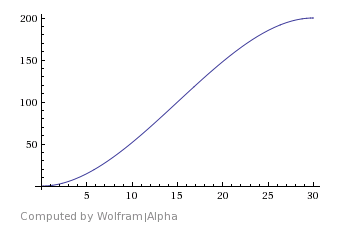
Make sure that we get the S-curve on the segment [0; T] . Substitute the values with = 1, r = 2, P = 100, N = 10 and get T = 30 .
Plot p = p (t) for Waterfall:

Graph s = s (t) for Waterfall:
Someone will consider this post captaincy, and will not be far from the truth. After all, of course, the models are slightly "cannibalistic", and do not take into account the changes (which, in essence, are updates of the plans). At the same time, if you collect a different number of people on Waterfall and Agile, the dates can be evened out, but the budgets will be different.
I will not say that Agile is optimal (despite the fact that this is an extreme time limit for such modeling) - there are too many simplifications in the models. But it is quite possible that the considered mechanics explain some difference between the effects with different approaches, and someone will adopt the considered principle to optimize their project plans: to involve as many people as possible to solve problems immediately - can reduce the time while maintaining the budget (although and it may seem like the budget will increase).
| Tip # 30: Count wherever possible. If the account is impossible - calculate. Use estimates derived from expert judgment alone, as a last resort. McConnell S. How much does a software project cost (2007). |
Prehistory
Management of the project, conditionally, can be divided into two components - the planning and control of the course.
')
From this point of view, everything is clear for waterfall - we compiled a step-by-step (analytics-development-testing) scheduling of tasks according to estimated deadlines, distributed tasks and implemented them forward.
With Scrum and Kanban it is slightly more difficult: the planning sequence is carried out through priorities in the backlog, development is controlled either through the burndown chart for the entire project (in Scrum), or using the lead time (in Kanban). Estimation of the complexity of the tasks entails an estimate of the dates - through the three iterations or tasks the speed becomes clear, on the basis of which it is possible to estimate the end date.
In this post, the course of the project will not be modeled (this is a completely separate task for itself), and the planned effectiveness will be compared.
"At the tip of the pen"
Let's present the plan as two components:
- The total number of units (analogue of storypoints) of the tasks for the entire product of the project ( P ),
- The number of personnel involved at the moment t n (t) <= N (equality in the case of Agile).
Further, we denote as r - the time to implement one unit of task complexity by one specialist, c is the cost of one specialist per time unit, T is the total project time, S is its budget, p = p (t) is the amount of work done at time t .
Then for Agile we have that for a unit of time we will do as much work as N people perform at a time task units:
p ' A (t) = N / r => (knowing that there is no work at first) p A (t) = N * t / r .
Where, in fact, the following is clear:
T A = r * P / N; S A (t) = c * N * t; S A = c * r * P.
it's all clear anyway
Obviously, how much a person will work, and to multiply by time, and by cost, the project will cost as much. At the same time, it costs as much as it costs to solve one task, multiplied by the number of tasks.
At this point, with Agile finished, fortunately, the model of his plan turned out to be (in my version) quite simple. Everything becomes more complicated with the Waterfall-plan, as it involves experts in the course of the project. In this case, however, remains the basic relationship:
p '(t) = n (t) / r .
It's all about the choice of the function n (t) . We know that at zero it is zero, and at the end of the project - zero. We know nothing more. Further, we will assume that it is symmetric, reaches the value of N in the middle, and grows quadratically (I chose the quadratic function from the considerations that this is the simplest variant under the given conditions).
n (t) = N * 4 * (T - t) * t / T 2 .
Knowing that p (0) = 0 , we can write out the integral p '(t) :
p (t) = 2 * N * t ^ 2 / (r * T) - 4 * N * t ^ 3 / (3 * r * T ^ 2) => T = 3 * P * r / (2 * N ) .
ABOUT! But this is already interesting! With the selected law of attracting the team to the project in time, the length of the project grows one and a half times! But the situation with the involvement of not all the staff at once is typical for Waterfall.
it's all intuitive again
It is clear that if people do the tasks right away, then this reduces the time. At the same time, if the maximum is involved all the time - N people - then this is the situation of a minimum for the project time.
What do we have with the cost? It can also be found by integrating (by t ).
s' (t) = c * n (t) => s (t) = 2 * c * N * t ^ 2 * (3 * T - 2 * t) / (3 * T ^ 2) ,
from where
S W = 2 * c * N * T / 3 = c * P * r .
The budget is the same.
not surprising
And why should he be different if the amount of work is the same?
Curves
Make sure that we get the S-curve on the segment [0; T] . Substitute the values with = 1, r = 2, P = 100, N = 10 and get T = 30 .
Plot p = p (t) for Waterfall:

Graph s = s (t) for Waterfall:

S-shaped curve
This is not a logistic curve , since our plan determines the amount of work done at a time, and not the number of people depends on how much work should be done at what time.
Few conclusions
Someone will consider this post captaincy, and will not be far from the truth. After all, of course, the models are slightly "cannibalistic", and do not take into account the changes (which, in essence, are updates of the plans). At the same time, if you collect a different number of people on Waterfall and Agile, the dates can be evened out, but the budgets will be different.
I will not say that Agile is optimal (despite the fact that this is an extreme time limit for such modeling) - there are too many simplifications in the models. But it is quite possible that the considered mechanics explain some difference between the effects with different approaches, and someone will adopt the considered principle to optimize their project plans: to involve as many people as possible to solve problems immediately - can reduce the time while maintaining the budget (although and it may seem like the budget will increase).
Source: https://habr.com/ru/post/226323/
All Articles