Geekly Articles each Day
📜 ⬆️ ⬇️

Axiom - raise the degree!

The old gray donkey Eeyore stood alone in the thistle-covered corner of the Forest, his front legs wide apart and his head hanging to the side, and thinking about Serious Things.

A. Milne "Winnie the Pooh and all-all-all"

- See the donkey? - I ask the policeman. - Over there is a little gray donkey ... Article 2908. Price thirty-two pennies. He has a great future.
- At donkeys it happens - the policeman agrees. - They sometimes have a very big future.
')
Heinrich Altov "Donkey and Axiom"


What is the most difficult in the development of board games? Obviously, no animation of moving figures on the board. It is difficult to come up with reasonable and interesting game rules. It can be very difficult to ensure a game balance. If we are engaged in computer development, it is often incredibly difficult to implement high-quality AI (for games like Go or Shogi, this problem has not been solved until now). And even if we managed to implement a working AI, we have to do a very large amount of work in order to evaluate the quality of its work and choose the best one from several possible options.

I want to talk about a tool that can significantly simplify the solution of all these issues. The Axiom Development Kit was conceived by developers as a way to improve Zillions of Games . In particular, it is focused on the implementation of games related to the capture of territory (such as Go), with which AI ZoG copes very poorly. In addition, the Axiom significantly expands the capabilities of ZoG developers, providing a lot of opportunities that are practically not implemented in the traditional ZRF (rule description language). With all this, the Axiom can work completely independently, even if ZoG has never been installed and purchased on a computer. But first things first…

In the image and likeness


I already wrote that ZoG has many flaws. Fortunately, the developers have provided a mechanism to cope with some of them. The extension module (engine) is a dynamically loaded library (DLL), taking control of all aspects of the game, except for its visualization. Here you can see an example of such an extension.

Developing your own extension yourself can be very time consuming. We'll have to develop AI (most likely in C ++), because when the engine is connected, the regular AI ZoG is disabled. Axiom is a programmable engine that implements such complex developer things as AI algorithms and provides an opportunity to focus on the game logic.

Let's try to implement the "Royal Game of Ur." A minimum ZRF file is required for operation:

Connecting engine
(version "2.0") (game (title "Ur") (engine "../Axiom/Ur/axiom.dll") (option "animate captures" false) (option "animate drops" false) (option "show moves list" false) (option "pass turn" forced) (option "highlight goals" false) (option "prevent flipping" true) (option "recycle captures" true) (drop-sound "Audio/Dice_cup.wav") (move-sound "Audio/Clack.wav") (capture-sound "") (players Black White ?Dice) (turn-order White ?Dice ?Dice ?Dice ?Dice Black ?Dice ?Dice ?Dice ?Dice) (board (image "Images\Ur\board.bmp") (grid (start-rectangle -503 -13 -442 79) (dimensions ("a/b/c/d/e/f/g/h/i/j/k/l/m/n/o/p/q" (67 0)) ; files ("5/4/3/2/1" (0 66)) ; ranks ) ) ) (board-setup (?Dice (wdice q4) (bdice q3 q2) (lock q1) ) (Black (init i5 j5 k5 l5 m5 n5 o5) ) (White (init i1 j1 k1 l1 m1 n1 o1) ) ) (piece (name lock) (image ?Dice "Images\Ur\invisible.bmp" Black "Images\Ur\invisible.bmp" White "Images\Ur\invisible.bmp") ) (piece (name init) (image Black "Images\Ur\binit.bmp" White "Images\Ur\winit.bmp") ) (piece (name prom) (image Black "Images\Ur\bprom.bmp" White "Images\Ur\wprom.bmp") ) (piece (name wdice) (image ?Dice "Images\Ur\wdice.bmp") ) (piece (name bdice) (image ?Dice "Images\Ur\bdice.bmp") ) ; The following dummy piece is required in order to placate the Zillions engine. ; It appears as though Zillions must find at least one "moves" keyword somewhere ; in the zrf in order for it to be happy and thus allow "moves" to work correctly. (piece (name Dummy) (dummy) (moves (from))) )


There remains a description of the players, a sequence of moves, pieces, but there is no description of the rules by which the pieces walk. Also there are no definitions of directions on the board, game zones, conditions for the completion of the game, and everything else associated with the game rules. All this will be contained in the scripts of the Axiom. The sad point is that the ZoG interface with the engine does not provide for the transfer of information contained in the ZRF file. This means that all these descriptions will have to be duplicated in Axiom scripts.

Fortunately, the Axiom Development Kit comes with a utility to automate this process. ZRF Converter is quite capricious at work. If he didn’t like something in the ZRF file (for example, the description of the board made in a macro), the conversion process is interrupted with a mysterious diagnosis, which makes me break my head. If everything went well, we get the following description at the output:

Ur.4th
 {board {position} a5 {position} b5 {position} c5 {position} d5 {position} e5 {position} f5 {position} g5 {position} h5 {position} i5 {position} j5 {position} k5 {position} l5 {position} m5 {position} n5 {position} o5 {position} p5 {position} q5 {position} a4 {position} b4 {position} c4 {position} d4 {position} e4 {position} f4 {position} g4 {position} h4 {position} i4 {position} j4 {position} k4 {position} l4 {position} m4 {position} n4 {position} o4 {position} p4 {position} q4 {position} a3 {position} b3 {position} c3 {position} d3 {position} e3 {position} f3 {position} g3 {position} h3 {position} i3 {position} j3 {position} k3 {position} l3 {position} m3 {position} n3 {position} o3 {position} p3 {position} q3 {position} a2 {position} b2 {position} c2 {position} d2 {position} e2 {position} f2 {position} g2 {position} h2 {position} i2 {position} j2 {position} k2 {position} l2 {position} m2 {position} n2 {position} o2 {position} p2 {position} q2 {position} a1 {position} b1 {position} c1 {position} d1 {position} e1 {position} f1 {position} g1 {position} h1 {position} i1 {position} j1 {position} k1 {position} l1 {position} m1 {position} n1 {position} o1 {position} p1 {position} q1 board} {players {player} Black {player} White {player} ?Dice {random} players} {pieces {piece} lock {piece} init {piece} prom {piece} wdice {piece} bdice {piece} Dummy pieces} {turn-order {repeat} {turn} White {turn} ?Dice {turn} ?Dice {turn} ?Dice {turn} ?Dice {turn} Black {turn} ?Dice {turn} ?Dice {turn} ?Dice {turn} ?Dice turn-order} {board-setup {setup} ?Dice wdice q4 {setup} ?Dice bdice q3 {setup} ?Dice bdice q2 {setup} ?Dice lock q1 {setup} Black init i5 {setup} Black init j5 {setup} Black init k5 {setup} Black init l5 {setup} Black init m5 {setup} Black init n5 {setup} Black init o5 {setup} White init i1 {setup} White init j1 {setup} White init k1 {setup} White init l1 {setup} White init m1 {setup} White init n1 {setup} White init o1 board-setup}


Here we are waiting for the first surprises. Axiom allows you to describe the board more compact, but with serious limitations. The grid design allows to describe only rectangular boards with the “standard” naming of cells (besides, only one grid can be used in the description of the board). If it is necessary to describe boards of a more complex form (for example, three-dimensional), you will have to explicitly describe each position in the way that ZRF Converter did. Since, in our case, all restrictions are observed (I had to rename the columns and rows of the board, compared to the ZRF implementation), we use a more compact entry:

 {board 5 17 {grid} board}

Further, it is necessary to determine the directions in which the figures can move. In games like Chess or Checkers, we could use a compact notation that defines directions in terms of coordinate increments:

 {directions -1 0 {direction} North 1 0 {direction} South 0 1 {direction} East 0 -1 {direction} West -1 1 {direction} Northeast 1 1 {direction} Southeast -1 -1 {direction} Northwest 1 -1 {direction} Southwest directions}

Alas, in our case, this method does not fit. Since the trajectory of the movement of chips on the board, in the game Ur, is rather bizarre, you will have to explicitly determine the connections between the positions:

Directions
 {directions ( Anext ) {link} Anext i1 l2 {link} Anext j1 l2 {link} Anext k1 l2 {link} Anext l1 l2 {link} Anext m1 l2 {link} Anext n1 l2 {link} Anext o1 l2 {link} Anext l2 k2 {link} Anext k2 j2 {link} Anext j2 i2 {link} Anext i2 i3 {link} Anext i3 j3 {link} Anext j3 k3 {link} Anext k3 l3 {link} Anext l3 m3 {link} Anext m3 n3 {link} Anext n3 o3 {link} Anext o3 o2 {link} Anext o2 p2 {link} Anext p2 p3 {link} Anext p3 p4 {link} Anext p4 o4 {link} Anext o4 o3 ( Bnext ) {link} Bnext i5 l4 {link} Bnext j5 l4 {link} Bnext k5 l4 {link} Bnext l5 l4 {link} Bnext m5 l4 {link} Bnext n5 l4 {link} Bnext o5 l4 {link} Bnext l4 k4 {link} Bnext k4 j4 {link} Bnext j4 i4 {link} Bnext i4 i3 {link} Bnext i3 j3 {link} Bnext j3 k3 {link} Bnext k3 l3 {link} Bnext l3 m3 {link} Bnext m3 n3 {link} Bnext n3 o3 {link} Bnext o3 o4 {link} Bnext o4 p4 {link} Bnext p4 p3 {link} Bnext p3 p2 {link} Bnext p2 o2 {link} Bnext o2 o3 ( Cnext ) {link} Cnext p3 p4 {link} Cnext p4 o4 {link} Cnext o4 o3 {link} Cnext o3 n3 {link} Cnext n3 m3 {link} Cnext m3 l3 {link} Cnext l3 k3 {link} Cnext k3 j3 {link} Cnext j3 i3 {link} Cnext i3 h3 ( Dnext ) {link} Dnext p3 p2 {link} Dnext p2 o2 {link} Dnext o2 o3 {link} Dnext o3 n3 {link} Dnext n3 m3 {link} Dnext m3 l3 {link} Dnext l3 k3 {link} Dnext k3 j3 {link} Dnext j3 i3 {link} Dnext i3 h3 directions}


Black and white pieces move in different ways, so I had to determine the direction Anext for white and Bnext for black pieces. In addition, for chips that have passed through the transformation field, it is necessary to define the directions Cnext and Dnext . If this is not done, a fork in the o3 field will form and all the chips will spin in a small block, choosing the first of the available routes.

 {symmetries Black {symmetry} Anext Bnext Black {symmetry} Cnext Dnext symmetries}

This design allows you to define "symmetry." A good illustration is the movement of pawns in Chess. Pawns always move “forward”, but for white it is a move up the board, and for black it is in the opposite direction. There are more complex forms of symmetry. For example, in four-sided versions of Chess, the movement “forward”, depending on the color, can occur in the direction of any of the four “cardinal points”. Having defined “symmetry”, we can always use the same direction (for example, Anext ), without paying attention to the color of the figure. For blacks, it will be automatically converted to symmetric ( Bnext ).

Fortification


My acquaintance with the Fort was early, but for a very long time remained very nodding. For the first time I saw a fort in the times of GK-nis and Mikrosh. My friend had Vector 06C , which we managed to pull away only behind the ears, with the joint efforts of all parents. To the Vector, periodically, cassettes with games were bought in addition, and from time to time a “unaccounted for” was found on them. Among such unaccounted for, we found the implementation of the Fort. Having played enough with the stack, my friend and I said “aha”, and established the base of the number system to zero (there is such a funny possibility in the Fort). The fort naturally could not transfer this and we forgot about it for a while.

Subsequently, already at the institute, the Fort repeatedly surfaced to the surface of my attention, but they could not be seriously dealt with. In fact, I never had a chance to come across any microcontroller programming with any other useful application of the Fort. And now, thanks to the developers of Axiom, I have the opportunity! The fact is that the word Forth appears in their ForthScript for a reason. In fact, both Axiom itself and part of ForthScript are implemented on Forte, and axiom.dll has an interpreter that allows them to be used. If necessary, in axiom.4th and CORE.4TH you can see the details of the implementation, and perhaps something to correct.

So, the entire game logic will have to be programmed at Forte. But where to start development? For a start, it would be nice to achieve a simple movement of the pieces on the board. Each figure must be able to move 1, 2, 3 or 4 cells along its path of movement (until we are distracted by throwing random points on the “bones”):

Movement of figures
 : common-move ( 'dir n -- ) SWAP BEGIN DUP EXECUTE verify SWAP 1- DUP 0= IF DROP TRUE ELSE SWAP FALSE ENDIF UNTIL empty? IF from here move add-move ENDIF ; : i-move-1 ( -- ) ['] Anext 1 common-move ; : i-move-2 ( -- ) ['] Anext 2 common-move ; : i-move-3 ( -- ) ['] Anext 3 common-move ; : i-move-4 ( -- ) ['] Anext 4 common-move ; : p-move-1 ( -- ) ['] Cnext 1 common-move ; : p-move-2 ( -- ) ['] Cnext 2 common-move ; : p-move-3 ( -- ) ['] Cnext 3 common-move ; : p-move-4 ( -- ) ['] Cnext 4 common-move ; {moves i-moves {move} i-move-1 {move} i-move-2 {move} i-move-3 {move} i-move-4 moves} {moves p-moves {move} p-move-1 {move} p-move-2 {move} p-move-3 {move} p-move-4 moves} {pieces {piece} init {moves} i-moves {piece} prom {moves} p-moves pieces}


By running ZRF-ku on execution, you can make sure that now the figures can be moved. How does all this work? Let's look at the implementation of common-move . A comment (in the style of the Fort), located immediately after the name, shows that it takes two parameters on the stack — the compiled command for moving in the direction and the number of moving steps. The implementation itself consists of two parts. First, in the cycle, a specified number of times, a transition in direction is performed, then, after verifying that the target field is empty, a sequence of Axiom commands are executed that form a move (moving a chip). The most important thing during all this balancing act is not to destroy the stack!

A description of each of the executed commands can be found in the ForthScript and Axiom manuals supplied with the Axiom Development Kit, I want to draw your attention to a couple of important differences between this code and what could be written using ZRF:


Having played with this version for some time, you can see that the chips, having reached a small block, begin to walk in a circle. In order for the chip to break out of this “circle of sansara”, it must be turned over (for inverted chips, the directions Cnext and Dnext are set , leading to the finish line). Let me remind you that turning the chips in the game Ur, tricky. The chip turns over without getting up on the transformation field, but passing through it. In addition, since the chips can now go all the way to the end, let's not forget about removing the chips that have reached the finish line from the board:

Chip Turning
 VARIABLE isPromouted : common-move ( 'dir n -- ) FALSE isPromouted ! SWAP BEGIN current-player White = IF here p2 ELSE here p4 ENDIF = IF TRUE isPromouted ! ENDIF DUP EXECUTE verify SWAP 1- DUP 0= IF DROP TRUE ELSE SWAP FALSE ENDIF UNTIL empty? IF from here move here h3 = IF capture ENDIF isPromouted @ IF current-piece-type 1+ change-type ENDIF add-move ENDIF ;


Here it is worth saying a few words about the variables in the Fort. We define the isPromouted variable using the VARIABLE keyword. After a variable is defined, any mention of it in the code pushes the address of this variable onto the stack. To retrieve the value located at the specified address, use the @ command, the command ! overwrites the value of a variable.

Some complexity, in Axiom, are manipulations with types of shapes. The fact is that the definitions of figures are located after the code that controls their movement (as they use it). For this reason, we cannot use the names of the types of shapes in the code (since they are not yet defined in this place). As a rule, you can get out of this unpleasant situation. For example, in our code, to turn the chips, we simply increment the type of the figure that performs the move.

An important part of the gameplay is the ability to skip the course of the players. The player is obliged to make a move if there is such an opportunity and skip the move, otherwise. If you do not take care of this on purpose, the game will be automatically ended in a draw at the first impossibility of the move by any of the players. Also, by skipping the opponent's turn, it is logical to realize the player’s repeated turn after the move to the “socket”. Let's do it:

Skip stroke
 : is-rosette? ( -- ? ) here i2 = here i4 = OR here l3 = OR here o2 = OR here o4 = OR ; : common-move ( 'dir n -- ) q5 enemy-at? NOT IF FALSE isPromouted ! SWAP BEGIN current-player White = IF here p2 ELSE here p4 ENDIF = IF TRUE isPromouted ! ENDIF DUP EXECUTE verify SWAP 1- DUP 0= IF DROP TRUE ELSE SWAP FALSE ENDIF UNTIL empty? IF from here move here h3 = IF capture ENDIF isPromouted @ IF current-piece-type 1+ change-type ENDIF is-rosette? IF q1 piece-type-at q5 create-piece-type-at ELSE q5 capture-at ENDIF add-move ENDIF ENDIF ; : pass-move ( -- ) q5 capture-at Pass add-move ; {moves i-moves {move} i-move-1 {move-type} normal-type {move} i-move-2 {move-type} normal-type {move} i-move-3 {move-type} normal-type {move} i-move-4 {move-type} normal-type {move} pass-move {move-type} pass-type moves} {moves p-moves {move} p-move-1 {move-type} normal-type {move} p-move-2 {move-type} normal-type {move} p-move-3 {move-type} normal-type {move} p-move-4 {move-type} normal-type {move} pass-move {move-type} pass-type moves} {move-priorities {move-priority} normal-type {move-priority} pass-type move-priorities}


First is the intricate definition of is-rosette? . Unfortunately, in Axiom, unlike ZRF, there is no possibility of defining gaming zones. All fields have to be checked individually.

Implementing a skip move is also different from the approach used in ZRF. The setting of the " pass turn " option is ignored by the Axiom. Instead, a pass must be formed explicitly with the Pass command. This is one example of more fully exploiting the notation of recording ZSG moves (used to transfer a move from the engine to the ZoG). Another such example is the possibility of using drop commands ( partial moves ) in partial moves (not implemented in ZRF).

Note
Understanding the ZSG notation is very important when developing your own extension modules ( engines ). The ability to perform any move in ZoG is completely determined by whether it can be written in ZSG notation. ZoG does not document this format, but the Axiom documentation has a section describing it (Appendix B). Familiarity with this section can save the developer from lengthy experiments in order to clarify the features of ZSG-notation.

In order to pass a move only if there is no possibility of any other move, it is necessary to use priorities. A move having a lower priority can only be executed if there is no possibility of a move with a higher priority. Unfortunately, the omission of the move in the Axiom style is functionally not fully equivalent to the behavior of ZoG, when setting the " pass turn " option to force . In the ZRF implementation, skipping a move is performed automatically; in the case of the Axiom, you have to press a button:



I have to say, this is pretty confusing.

To implement a pass after the move, an invisible lock figure is placed at the q5 position that is not used in the game. At the very beginning of the common-move , it checks for the presence of an enemy figure in this field. If the field is occupied by the enemy - the course is impossible.

Now, it's time to learn how to throw “bones”:

Bone roll
 {players {player} White {player} Black {player} ?Dice {random} players} {turn-order {turn} White {turn} ?Dice {of-type} clear-type {turn} ?Dice {turn} ?Dice {turn} ?Dice {turn} Black {turn} ?Dice {of-type} clear-type {turn} ?Dice {turn} ?Dice {turn} ?Dice turn-order} : drop-dices ( -- ) q2 here = q3 here = OR q4 here = OR empty? AND IF drop add-move ENDIF ; : count-dices ( -- n ) q2 piece-at piece-value q3 piece-at piece-value + q4 piece-at piece-value + DUP 0= IF DROP 4 ENDIF ; : clear-dices ( -- ) q1 here = verify q2 not-empty-at? q3 not-empty-at? q4 not-empty-at? AND AND IF drop q2 capture-at q3 capture-at q4 capture-at add-move ENDIF ; : i-move ( -- ) ['] Anext count-dices common-move ; : p-move ( -- ) ['] Cnext count-dices common-move ; {moves p-moves {move} p-move {move-type} normal-type {move} pass-move {move-type} pass-type moves} {moves drops {move} drop-dices {move-type} normal-type {move} pass-move {move-type} pass-type moves} {moves clears {move} clear-dices {move-type} clear-type moves} {pieces {piece} lock {moves} clears {piece} init {moves} i-moves {piece} prom {moves} p-moves {piece} wdice {drops} drops 1 {value} {piece} bdice {drops} drops 0 {value} pieces}


Throwing "bones" ( drop-dices ) is done elementary. Just check that the target field is intended to roll the dice, set the figure with the drop command and end the move with the add-move command. Clearing is somewhat more complicated ( clear-dices ). In ZoG, there is no possibility to form a move consisting only in removing a piece from the board. We associate the cleaning stroke with resetting an invisible piece to the q1 field that is not used in the game. Removing bones from the board is a side effect of this move. It remains to calculate the dropped points ( count-dices ) and pass this value to common-move .

In order to determine the condition of the completion of the game, it is necessary to count the chips that have left the board. The completion check itself is performed by the Axiom by calling the overridden word OnIsGameOver . To perform the initial actions, when starting the game (for example, initializing a pseudo-random number generator), you must override OnNewGame :

Termination condition
 {board 5 17 {grid} {variable} WhitePieces {variable} BlackPieces board} : WhitePieces++ WhitePieces ++ ; : BlackPieces++ BlackPieces ++ ; : common-move ( 'dir n -- ) q5 enemy-at? NOT IF FALSE isPromouted ! SWAP BEGIN current-player White = IF here p2 ELSE here p4 ENDIF = IF TRUE isPromouted ! ENDIF DUP EXECUTE verify SWAP 1- DUP 0= IF DROP TRUE ELSE SWAP FALSE ENDIF UNTIL empty? IF from here move here h3 = IF current-player White = IF COMPILE WhitePieces++ ELSE COMPILE BlackPieces++ ENDIF capture ENDIF isPromouted @ IF current-piece-type 1+ change-type ENDIF is-rosette? IF q1 piece-type-at q5 create-piece-type-at ELSE q5 capture-at ENDIF add-move ENDIF ENDIF ; : OnNewGame ( -- ) RANDOMIZE ; : OnIsGameOver ( -- gameResult ) repetition-reset #UnknownScore current-player White = IF BlackPieces @ 7 - 0= IF DROP #LossScore ENDIF ENDIF current-player Black = IF WhitePieces @ 7 - 0= IF DROP #LossScore ENDIF ENDIF ;


Note
The use of variables defined “on the board” is described in Section 3.9.4 “Updating Board Variables” of the Axiom documentation.

To get a full-fledged game, it remains to realize the battle of figures and the processing of special fields. I will not clutter the article with these details, since they do not carry anything fundamentally new. Those interested can see the full implementation of the “Royal Game of Ur” on GitHub .

The basic Instinct


The main highlight of ZoG is its versatility. ZRF allows you to create a new game (or describe an existing one) simply by declaring its rules. Yes, it plays noticeably worse than specialized programs, but the similar possibility of quickly creating a prototype for almost any game is worth a lot! The number of applications developed for ZoG speaks for itself.

Axiom is also versatile. It removes many of the unpleasant limitations of ZoG and allows you to describe such board games that ZoG cannot cope with. One possibility of using full-fledged arithmetic, instead of manipulating with boolean flags, brings this product to a qualitatively higher level, but this is not the main advantage of Axiom! ZoG plays good or bad, but for us its AI is a black box. We can not affect the quality of his game! Axiom gives us the opportunity (but does not require it) to participate in the development of algorithms for choosing the optimal course.

The most obvious possibility of interfering with the work of AI Axiom is the choice of a weight function, with the help of which each position is evaluated. We are only required to override OnEvaluate . Let's try to create a very simple evaluation function, taking as a basis the total advancement of the chips from start to finish. Placement of chips on the starting position will be weighted with a weight of 0, and chips that have passed the full path will be evaluated by some large number, for example 100. Obviously, if some chip is taken, the value of the assessment will decrease sharply (the more, the further the chip has move forward). Of course, for the enemy we will use the same estimate, taken with the opposite sign. The better the position of the enemy - the worse our:

Simple evaluation function
 VARIABLE whiteScored VARIABLE blackScored : Score ( value piece-type player pos -- score ) DUP not-empty-at? IF DUP player-at White = IF whiteScored -- ELSE blackScored -- ENDIF DUP ROT SWAP player-at = ROT ROT piece-type-at = AND NOT IF DROP 0 ENDIF ELSE DROP DROP DROP DROP 0 ENDIF ; : OnEvaluate ( -- score ) 7 whiteScored ! 7 blackScored ! 0 1 White i1 Score 0 1 White j1 Score + 0 1 White k1 Score + 0 1 White l1 Score + 0 1 White m1 Score + 0 1 White n1 Score + 0 1 White o1 Score + 0 1 Black i5 Score + 0 1 Black j5 Score + 0 1 Black k5 Score + 0 1 Black l5 Score + 0 1 Black m5 Score + 0 1 Black n5 Score + 0 1 Black o5 Score + 1 1 White l2 Score + -1 1 Black l4 Score + 2 1 White k2 Score + -2 1 Black k4 Score + 3 1 White j2 Score + -3 1 Black j4 Score + 4 1 White i2 Score + -4 1 Black i4 Score + 5 1 White i3 Score + -5 1 Black i3 Score + 6 1 White j3 Score + -6 1 Black j3 Score + 7 1 White k3 Score + -7 1 Black k3 Score + 8 1 White l3 Score + -8 1 Black l3 Score + 9 1 White m3 Score + -9 1 Black m3 Score + 10 1 White n3 Score + -10 1 Black n3 Score + 11 1 White o3 Score + -11 1 Black o3 Score + 12 1 White o2 Score + -12 1 Black o4 Score + 13 1 White p2 Score + -13 1 Black p4 Score + 14 2 White p3 Score + -14 2 Black p3 Score + 15 2 White p4 Score + -15 2 Black p2 Score + 16 2 White o4 Score + -16 2 Black o2 Score + 17 2 White o3 Score + -17 2 Black o3 Score + 18 2 White n3 Score + -18 2 Black n3 Score + 19 2 White m3 Score + -19 2 Black m3 Score + 20 2 White l3 Score + -20 2 Black l3 Score + 21 2 White k3 Score + -21 2 Black k3 Score + 22 2 White j3 Score + -22 2 Black j3 Score + 23 2 White i3 Score + -23 2 Black i3 Score + 1 1 White c2 Score + 1 1 White c3 Score + 1 1 White c4 Score + -1 1 Black d2 Score + -1 1 Black d3 Score + -1 1 Black d4 Score + 3 1 White a2 Score + 3 1 White a3 Score + 3 1 White a4 Score + -3 1 Black b2 Score + -3 1 Black b3 Score + -3 1 Black b4 Score + 7 1 White f2 Score + 7 1 White f3 Score + 7 1 White f4 Score + -7 1 Black f2 Score + -7 1 Black f3 Score + -7 1 Black f4 Score + 10 1 White g2 Score + 10 1 White g3 Score + 10 1 White g4 Score + -10 1 Black g2 Score + -10 1 Black g3 Score + -10 1 Black g4 Score + 11 1 White e2 Score + 11 1 White e3 Score + 11 1 White e4 Score + -11 1 Black e2 Score + -11 1 Black e3 Score + -11 1 Black e4 Score + 17 2 White e2 Score + 17 2 White e3 Score + 17 2 White e4 Score + -17 2 Black e2 Score + -17 2 Black e3 Score + -17 2 Black e4 Score + 18 2 White g2 Score + 18 2 White g3 Score + 18 2 White g4 Score + -18 2 Black g2 Score + -18 2 Black g3 Score + -18 2 Black g4 Score + 21 2 White f2 Score + 21 2 White f3 Score + 21 2 White f4 Score + -21 2 Black f2 Score + -21 2 Black f3 Score + -21 2 Black f4 Score + whiteScored @ 100 * + blackScored @ 100 * - current-player Black = IF NEGATE ENDIF ;


Of course, Axiom does not leave us alone with the Fort in developing the evaluation function. We are provided with convenient primitives for evaluating both material and positional components. For example, the following evaluation function (up to coefficients), taken from the official manual, will work well for most games, like Checkers and Chess:

 : Mobility ( -- mobilityScore ) move-count \ Number of moves available to us. current-player TRUE 0 $GenerateMoves \ Generate moves for opponent move-count \ Number of moves available to opponent. - \ #friendlyMoves - #unfriendlyMoves $DeallocateMoves \ Deallocate the opponent's move list ; : OnEvaluate ( -- score ) Mobility current-player material-balance 3 * + ;

Here the call move-count counts the number of possible moves from the current position, and material-balance calculates the sum of the weights assigned to the shapes using the {value} attribute (in our code, we use it to set numeric values ​​to the “bones”).

All this is fine, but what about when the use of the minimax algorithm itself is redundant? In the game that we are trying to implement, peeking more than one move forward will most likely lead only to a waste of computational resources. As i wrote, here we need not “Artificial Intelligence”, but rather “Artificial Instinct”! Axiom gives us the opportunity to intervene in the course selection algorithm at a deeper level:

Arbitrary stroke selection algorithm
 VARIABLE BestScore \ Keep track of the best score found so far by our search engine. VARIABLE Nodes \ The number of possibilities explored by our search engine. VARIABLE Eated VARIABLE Rosettes : enemy-value-at ( pos -- value ) DUP empty-at? IF DROP 0 ELSE 0 SWAP player-at current-player <> IF DROP 1 ENDIF ENDIF ; : friend-value-at ( pos -- value ) DUP empty-at? IF DROP 0 ELSE 1 SWAP player-at current-player <> IF DROP 0 ENDIF ENDIF ; : Make_enemy_p ( pos -- ) <BUILDS , DOES> @ enemy-value-at ; : Make_friend_p ( pos -- ) <BUILDS , DOES> @ enemy-value-at ; i1 Make_enemy_p e0 j1 Make_enemy_p e1 k1 Make_enemy_p e2 l1 Make_enemy_p e3 m1 Make_enemy_p e4 n1 Make_enemy_p e5 o1 Make_enemy_p e6 i5 Make_enemy_p e7 j5 Make_enemy_p e8 k5 Make_enemy_p e9 l5 Make_enemy_p e10 m5 Make_enemy_p e11 n5 Make_enemy_p e12 o5 Make_enemy_p e13 i2 Make_friend_p r0 i4 Make_friend_p r1 l3 Make_friend_p r2 o2 Make_friend_p r3 o4 Make_friend_p r4 : CountEated ( -- count ) e0 e1 + e2 + e3 + e4 + e5 + e6 + e7 + e8 + e9 + e10 + e11 + e12 + e13 + ; : CountRosettes ( -- count ) r0 r1 + r2 + r3 + r4 + ; : Score ( -- score ) Eated @ CountEated < IF 10 ELSE 0 ENDIF Rosettes @ CountRosettes < IF 5 ELSE 0 ENDIF + ; : Custom-Engine ( -- ) -1000 BestScore ! \ Keep track of the best score. 0 Nodes ! \ Count the number of possibilities explored. CountEated Eated ! CountRosettes Rosettes ! ( Notes: 1 - We do not need to invoke $GenerateMoves since they have already been generated for the current player { since ZoG has called DLL_GenerateMoves prior to calling DLL_Search}. 2 - ZoG does not invoke the search engine if there are no moves, so we can safely assume. that at least one move exists. Thus we can use BEGIN..UNTIL instead of BEGIN...WHILE..REPEAT for iterating moves. ) $FirstMove \ Obtain the address of the first move. BEGIN $CloneBoard \ Create a temporary copy of the current board. DUP $MoveString CurrentMove! \ Inform ZoG of the current move being examined. DUP .moveCFA EXECUTE \ Apply the move to the board by executing its code. Score \ Calculate the score for the new board. BestScore @ OVER < \ Have we found a better score? IF DUP BestScore ! \ Save the improved score. Score! \ Inform ZoG of the improved score. DUP $MoveString BestMove! ELSE DROP \ We didn't find a better move, drop the score. ENDIF $DeallocateBoard \ Done with the revised board. Nodes ++ \ Count one more node explored. Nodes @ Nodes! \ Inform ZoG of the node count. $Yield \ Allow ZoG to dispatch Windows messages. $NextMove \ Advance to the next move. DUP NOT \ No more moves? UNTIL DROP ; {players {player} White {search-engine} Custom-Engine {player} Black {search-engine} Custom-Engine {player} ?Dice {random} players}


Most of this code is taken from the documentation. As is clear from the comments, we iterate over all possible moves, and apply the evaluation function to the constructed temporary positions. As an evaluation function, we could take the same function that we wrote for OnEvaluate , but that would not be interesting. I tried to formulate some extremely aggressive strategy of the game. If there is an opportunity to take an enemy figure or stand on the "socket", this move is considered preferable, if there is no such possibility, the first available move is selected.

By the way, the primitive game strategies {first} and {random} predefined by Axiom are implemented in the same way. Here is how they are described in axiom.4th:

Primitive game strategies
 : $RandomMoveEngine $FirstMove 0 $movesList @ CELLSIZE + @ 1- $RAND-WITHIN BEGIN DUP 0> WHILE SWAP @ SWAP $Yield 1- REPEAT DROP ( move ) $MoveString DUP CurrentMove! BestMove! 1 Nodes! 0 Score! 0 Depth! ; : {random} ['] $RandomMoveEngine $CompileEngine ; : $FirstMoveEngine $FirstMove $MoveString DUP CurrentMove! BestMove! $Yield ; : {first} ['] $FirstMoveEngine $CompileEngine ;


As I said, open source (even if only partially) source code is great!

Lies, brazen lies and statistics


Well, we created a new game and can play it using ZoG. We have implemented several variants of the game with different turn-pick algorithms, but how do we determine which one is better? Of course, you can collect a dozen "experts" and ask each of them to play a hundred times with each of the options. As one of my friends said, "this can take years." There is a better way!

Axiom provides the AutoPlay utility that automates the testing process. The first thing we have to do, following the path of automation, is the creation of game variants :

 (variant (title "Ur [random]")) (variant (title "Ur [simple evaluation]")) (variant (title "Ur [aggressive]"))

Having added these lines to the end of the ZRF file, we will rerun ZRF Converter to get the presets for the 4th files of the game variants. These files need to be modified to influence the strategy used by the program. So, for example, one of the simplest options looks like:

 LOAD Ur.4th ( Load the base Ur game ) {players {player} White {random} {player} Black {random} {player} ?Dice {random} players}

As it is easy to see, we can redefine the individual sections of the description, putting all the shared code into loadable script files.

After the options are created, we can start the game in the game mode of one option against another. This is the main advantage of AutoPlay! You do not need to create variations in which players play using different strategies. It is enough to give the following command:

 AutoPlay Ur-[random] Ur-[random] 100

Everything is as simple as possible. We set options for the first and second players (in the current implementation of AutoPlay more players are not supported) and the number of games. Then the program works by itself. And she does it much faster than if these games were played using ZoG! At the output, a large text file is generated containing a description of all the games played in ZSG notation. At the very end, the final statistics is displayed, according to which one can see that provided that the moves are chosen randomly, the player making the first move has a slight advantage (even taking into account the fact that he always goes to the “one”):

 Final results: Player 1 "Ur-[random]", wins = 52. Player 2 "Ur-[random]", wins = 48. Draws = 0 100 game(s) played

Having a complete ZSG description allows us, after a little processing, to load any of the batches into ZoG and examine it step by step. By the way, it was in this way that these implementation errors were found and corrected (I don’t know what I thought when I decided to just drop the transition result instead of checking it).

Another advantage of having a full ZSG description is that, after processing the data, we can collect any necessary statistics if we are not satisfied with the simple ratio of the number of won / lost games. The following script displays the data on the duration of the games, the final score at the end of the game, the number of skips and the number of chips "felled" by each of the players:

Data processing script
 #!/usr/bin/perl -w my @S = (0, 0, 0, 0, 0, 0); my $ix = 0; my $T; while (<>) { if (/results/) { my $d = $S[0] - $S[1]; print "$T, $d, $S[3], $S[2], $S[4], $S[5]\n"; @S = (0, 0, 0, 0, 0, 0); $ix = 0; } else { if (/^(\d+)\.\s+[^?].*$/) { $T = $1; if (/x h3/) { $S[$ix]++; } if (/Pass|^(\d+)\.\s+x\s+q5\s*$/) { $S[$ix + 2]++; } if (/Black init [ijklmno]5/) { $S[4]++; } if (/White init [ijklmno]1/) { $S[5]++; } $ix++; if ($ix > 1) { $ix = 0; } } } }


Now we have everything you need to compare the quality of the game options developed by us. We will consider three options:


random vs random
( , , 150 ):



, ( — ):



«» :



, , , :

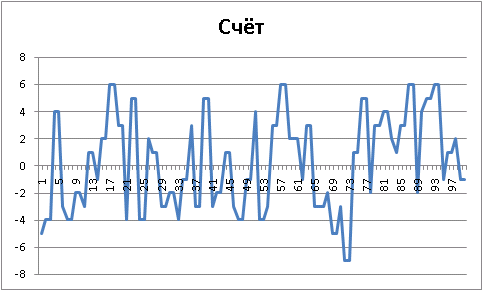
 Final results: Player 1 "Ur-[random]", wins = 52. Player 2 "Ur-[random]", wins = 48. Draws = 0 100 game(s) played


random vs simple
:



:

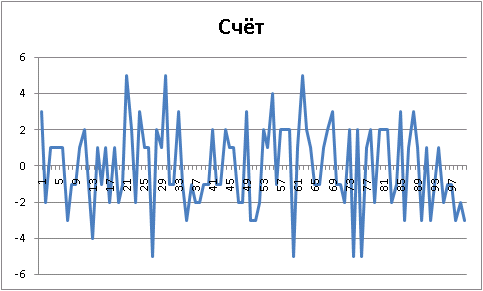
 Final results: Player 1 "Ur-[random]", wins = 50. Player 2 "Ur-[simple-evaluation]", wins = 50. Draws = 0 100 game(s) played


simple vs random
:



«» :



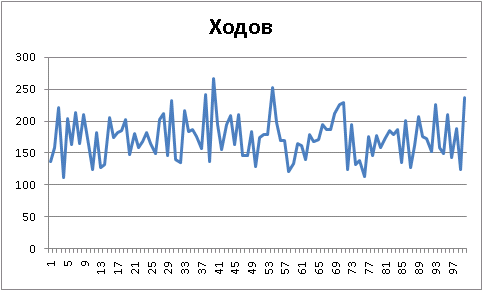
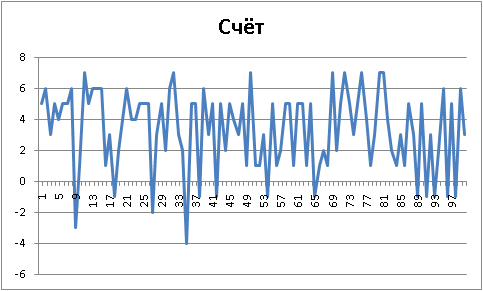
 Final results: Player 1 "Ur-[simple-evaluation]", wins = 87. Player 2 "Ur-[random]", wins = 13. Draws = 0 100 game(s) played


random vs agressive
:



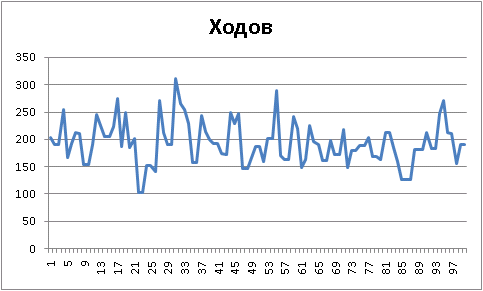
random ( ):



, , «» :



«» , !

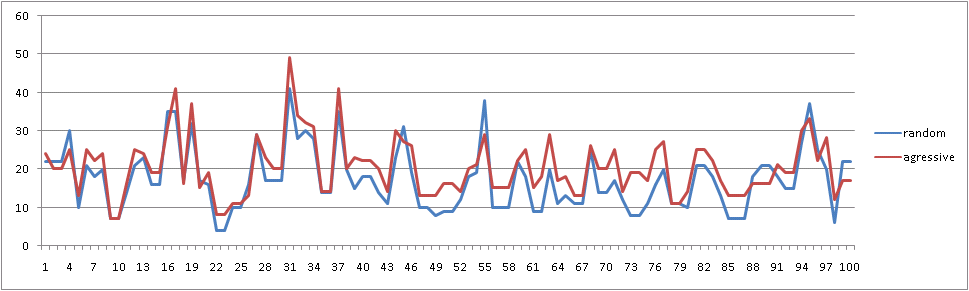
 Final results: Player 1 "Ur-[random]", wins = 25. Player 2 "Ur-[aggressive]", wins = 75. Draws = 0 100 game(s) played


agressive vs random
:



«» «» !



, «» , :



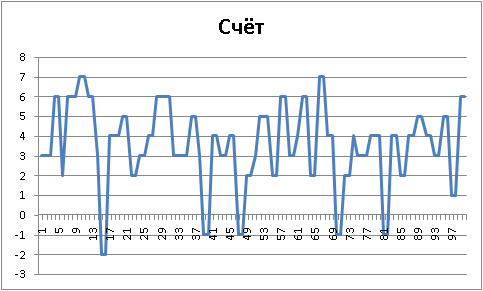
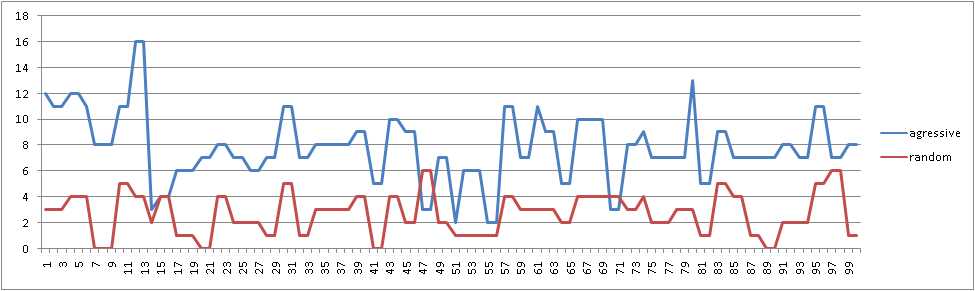
 Final results: Player 1 "Ur-[aggressive]", wins = 90. Player 2 "Ur-[random]", wins = 10. Draws = 0 100 game(s) played


simple vs agressive
, . , simple :



!



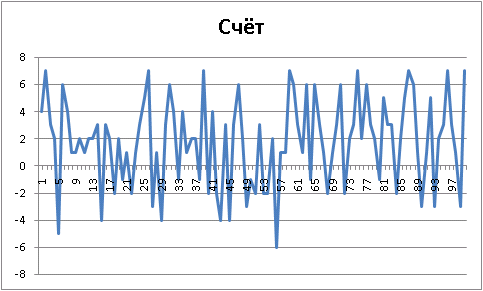
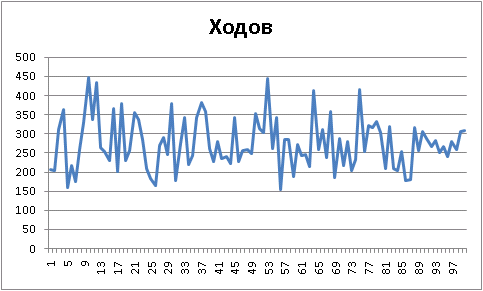
 Final results: Player 1 "Ur-[simple-evaluation]", wins = 73. Player 2 "Ur-[aggressive]", wins = 27. Draws = 0 100 game(s) played


agressive vs simple
, agressive :



«» , , «»:



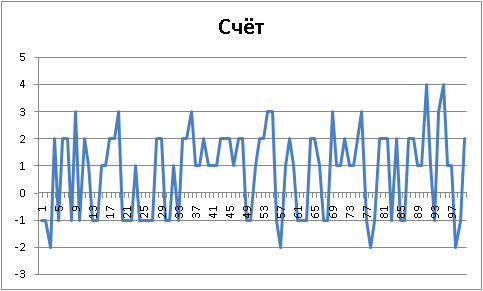
 Final results: Player 1 "Ur-[aggressive]", wins = 64. Player 2 "Ur-[simple-evaluation]", wins = 36. Draws = 0 100 game(s) played


By the way, pay attention to the following wonderful line:

 Draws = 0

The fact is that Axiom offers a way to combat 3-Time Repetition Draw! I carefully studied the relevant section of the documentation and took all the necessary actions. The problem is that in ZoG this situation still arises. This usually happens when long chains (3-4 chips in a row) of white and black chips block each other. In the "Royal Ur", thanks to the safe fields, there is always a way to disperse for them, but ZoG (even under the control of Axiom) does not wait until the chips disperse! But AutoPlay, play all the games until the end. In principle, as I have already said, it can be launched even without an installed and purchased ZoG, there will simply be no graphical interface.

... and a thousand elephants!


Of course, just in one article it is impossible to tell everything about such a complex and multifaceted product as the Axiom Development Kit. See what features are announced by the developers:

Axiom Engine Features
  • Contains a universal game engine designed to play a large variety of games. The search engine is not optimized for any particular class of games.
  • Allows (actually requires) the game programmer to specify a custom game AI. This is one of the main benefits of Axiom. Some 'built-in' AI helpers are provided. For example, one helper is simply the difference between the number of available moves for each player, another takes into consideration material advantage. The list is expected to grow over time.
  • «Minimax with Alpha-Beta pruning» search algorithm.
  • Iterative deepening with transposition table.
  • Zobrist hashing
  • Limited move reordering based on 'best move from previous iteration' stored in the transposition table.
  • Full width searching.
  • Support for 'partial' and 'pass' moves.
  • Supports 'teams'.
  • Time management.
  • Supports additional user-supplied custom engines.
  • Programmer controlled quiescence (currently experimental)

There is both time control support and team play support, which were so lacking in ZoG. Axiom provides a special data structure (Ring Buffer) for the development of “connection” and “territory capture” games. Somewhat frustrating is the fact that the attributes of figures are not supported (using which, for example, chess castling is implemented in ZoG), but Axiom provides enough opportunities to circumvent this unfortunate restriction.

Separate and very warm words deserve the quality of documentation and examples. Very complex material presented in such a way that its assimilation is not associated with any difficulties. And even if this material is not enough, the ZoG website has more than 60 of the most interesting applications developed using Axiom, available for analysis and study.

Source: https://habr.com/ru/post/226235/

More articles:


All Articles