Geekly Articles each Day
📜 ⬆️ ⬇️

Speech Recognition for Dummies


In this article I want to consider the basics of such an interesting area of ​​software development as Speech Recognition. Naturally, I am not an expert in this topic, so my story will be replete with inaccuracies, mistakes and disappointments. However, the main purpose of my “work”, as the name implies, is not a professional analysis of the problem, but a description of the basic concepts, problems and their solutions. In general, I ask all interested in welcome under the cut!



Prologue


')
To begin with, our speech is a sequence of sounds. Sound, in turn, is a superposition (superposition) of sound vibrations (waves) of various frequencies. The wave, as we know from physics, is characterized by two attributes - amplitude and frequency.



In order to save the audio signal on a digital medium, it must be divided into many gaps and take some "average" value on each of them.



In this way, mechanical vibrations are transformed into a set of numbers suitable for processing on modern computers.

It follows that the task of speech recognition is reduced to “matching” a set of numerical values ​​(digital signal) and words from a certain dictionary (Russian, for example).

Let's see how, in fact, this very "comparison" can be implemented.



Input data



Suppose we have some file / stream with audio data. First of all, we need to understand how it works and how to read it. Let's look at the simplest option - WAV file.



The format implies the presence of two blocks in the file. The first block is a header with information about the audio stream: bitrate, frequency, number of channels, file length, etc. The second block consists of “raw” data - that same digital signal, a set of amplitude values.

The logic of reading data in this case is quite simple. We read the header, check some restrictions (no compression, for example), save the data to a dedicated array.

An example .



Recognition



Purely theoretically, now we can compare (element by element) the sample we have with some other, the text of which we already know. That is, try to “recognize” the speech ... But it is better not to do it :)

Our approach should be sustainable (well, at least a little) to change the timbre of the voice (the person who utters the word), volume and speed of pronunciation. By element-wise comparison of two audio signals, this, naturally, cannot be achieved.

Therefore, we will go a little different way.



Frames



First of all, we divide our data by small time intervals - frames. And the frames should not go strictly one after another, but “overlapped”. Those. the end of one frame should intersect with the beginning of another.

Frames are a more suitable unit of data analysis than specific signal values, since it is much more convenient to analyze the waves at a certain interval than at specific points. The location of the overlapping frames makes it possible to smooth the results of frame analysis, turning the frame idea into a “window” moving along the original function (signal values).

It has been experimentally established that the optimal frame length should correspond to a gap of 10ms, an “overlap” of 50%. Taking into account the fact that the average word length (at least in my experiments) is 500ms - this step will give us approximately 500 / (10 * 0.5) = 100 frames per word.



Word splitting



The first task, which has to be solved in speech recognition, is the partitioning of this very speech into separate words. For simplicity, suppose that in our case it contains some pauses (intervals of silence), which can be considered as “delimiters” of words.

In this case, we need to find some value, the threshold - the values ​​above which are a word, below - silence. There may be several options:



As you have already guessed, we are now talking about the last point :) Let's start with the fact that entropy is a measure of confusion, “a measure of the uncertainty of any experience” (c). In our case, entropy means how strongly our signal oscillates within a given frame.

In order to calculate the entropy of a specific frame, perform the following actions:

calculate entropy as ;



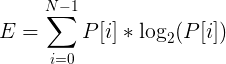An example .

And so, we got the value of entropy. But this is just one more characteristic of the frame, and in order to separate the sound from the silence, we still need to compare it with something. In some articles, it is recommended to take the entropy threshold equal to the average between its maximum and minimum values ​​(among all frames). However, in my case, this approach did not give any good results.
Fortunately, entropy (in contrast to the same mean square of values) is a relatively independent value. That allowed me to choose the value of its threshold in the form of a constant (0.1).

Nevertheless, the problems do not end there: (Entropy can sag in the middle of a word (on vowels), and can suddenly jump because of a small noise. In order to deal with the first problem, you have to introduce the concept of “minimum distance between words” and “glue” near recumbent framesets, separated due to sagging. The second problem is solved by using the “minimum word length” and cutting off all candidates that did not pass the selection (and not used in the first paragraph).

If, in principle, speech is not “articulate”, one can try to split the initial frame set into certain prepared subsequences, each of which will be subjected to a recognition procedure. But that's another story :)



Mfcc



And so, we have a set of frames corresponding to a certain word. We can take the path of least resistance and use the mean square of all its values ​​(Root Mean Square) as the numerical characteristic of a frame. However, such a metric carries very little information suitable for further analysis.

This is where the Mel-frequency cepstral coefficients come into play. According to Wikipedia (which, as you know, it does not lie), the MFCC is a unique representation of the energy of the signal spectrum. The advantages of its use are as follows:



Let's look at the process of calculating the MFCC coefficients for a frame.

Imagine our frame as a vector 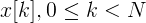where N is the frame size.



Fourier series expansion



First of all, we calculate the signal spectrum using the discrete Fourier transform (preferably with its “fast” FFT implementation).



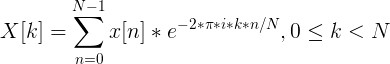
It is also recommended to apply the Hamming window function to the obtained values ​​in order to “smooth out” the values ​​at the frame boundaries.



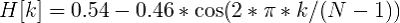
That is, the result will be a vector of the following form:



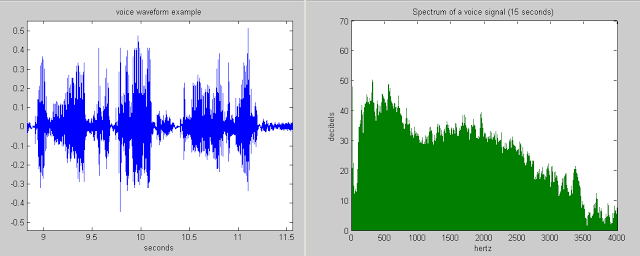
It is important to understand that after this transformation along the X axis we have the frequency (hz) of the signal, and along the Y axis - the magnitude (as a way to get away from the complex values):





Calculation of mel filters



Let's start with what mel. Again, according to Wikipedia, mel is a “psychophysical unit of pitch”, based on the subjective perception of the average people. It depends primarily on the frequency of the sound (as well as on the volume and tone). In other words, this value shows how much a sound of a certain frequency is “significant” for us.

You can convert the frequency into chalk using the following formula (let's remember it as “formula-1”):


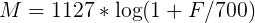
The inverse transform looks like this (remember it as “formula-2”):


Plot of mel / frequency:


But back to our problem. Suppose we have a frame size of 256 elements. We know (from the audio format data) that the frequency of the sound in this frame is 16000hz. Suppose that human speech is in the range of [300; 8000] hz. The number of the desired chalk coefficients put M = 10 (recommended value).

In order to decompose the spectrum obtained above on the mel scale, we will need to create a “comb” of filters. In fact, each mel-filter is a triangular window function that allows you to sum up the amount of energy at a certain frequency range and thereby get a mel-coefficient. Knowing the number of chalk coefficients and the analyzed frequency range, we can build a set of such filters:



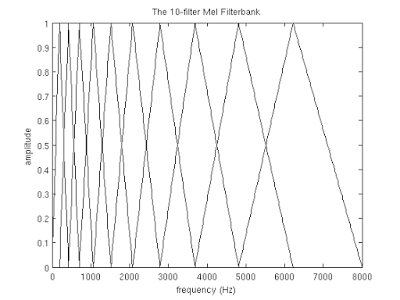
Note that the higher the number of the chalk factor, the wider the filter base. This is due to the fact that the division of the frequency range of interest to the ranges processed by the filters occurs on the chalk scale.

But we were distracted again. And so for our case, the range of frequencies of interest to us is equal to [300, 8000]. According to the formula-1 in on a chalk-scale, this range turns into [401.25; 2834.99].

Further, in order to build 10 triangular filters, we need 12 reference points:
m [i] = [401.25, 622.50, 843.75, 1065.00, 1286.25, 1507.50, 1728.74, 1949.99, 2171.24, 2392.49, 2613.74, 2834.99]


Notice that the points on the chalk scale are evenly spaced. Let's translate the scale back to hertz using formula-2:

h [i] = [300, 517.33, 781.90, 1103.97, 1496.04, 1973.32, 2554.33, 3261.62, 4122.63, 5170.76, 6446.70, 8000]


As you can see now the scale began to gradually stretch, thereby aligning the dynamics of growth of “significance” at low and high frequencies.

Now we need to impose the resulting scale on the spectrum of our frame. As we remember, along the X axis we have the frequency. The length of the spectrum of 256 - elements, while it fits 16000hz. Having solved a simple proportion, you can get the following formula:

f (i) = floor ((frameSize + 1) * h (i) / sampleRate)


which in our case is equivalent to

f (i) = 4, 8, 12, 17, 23, 31, 40, 52, 66, 82, 103, 128


That's all! Knowing the reference points on the X axis of our spectrum, it is easy to construct the filters we need using the following formula:





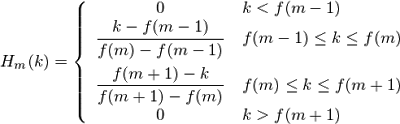
Apply filters, log energy spectrum



The application of the filter consists in pairwise multiplying its values ​​with the values ​​of the spectrum. The result of this operation is the mel coefficient. Since we have M filters, the coefficients will be the same.



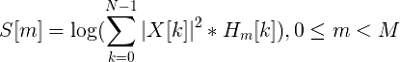
However, we need to apply mel-filters not to the values ​​of the spectrum, but to its energy. After that, the results obtained are prologized. It is believed that this reduces the sensitivity of the coefficients to noise.



Cosine transform



The discrete cosine transform (DCT) is used to get those same “cepstral” coefficients. Its meaning is to “compress” the results obtained, increasing the significance of the first coefficients and decreasing the significance of the latter.

In this case, DCTII is used without any multiplication by (scale factor).



Now for each frame we have a set of M mfcc coefficients that can be used for further analysis.

Examples of code for overlying methods can be found here .



Recognition algorithm



Here, dear reader, the main disappointment awaits you. I have seen on the Internet a lot of highly intelligent (and not so) debates about which method of recognition is better. Someone is in favor of Hidden Markov Models, some are for neural networks, whose thoughts are in principle impossible to understand :)

In any case, a lot of preferences are given to the SMM , and it is their implementation that I am going to add to my code ... in the future :)

At the moment, I propose to stop at a much less efficient, but at times more simple way.

And so, remember that our task is to recognize a word from a certain dictionary. For simplicity, we will recognize the naming of the first ten numbers: “one“, “two“, “three“, “four“, “five“, “six“, “seven“, “eight“, “nine“, “ten“.

Now we will take an iPhone / android in our hands and go through L colleagues asking them to dictate these words under the entry. Next, we assign (in some local database or a simple file) to each word L the sets of mfcc coefficients of the corresponding records.

We will call this correspondence “Model”, and the process itself - Machine Learning! In fact, the simple addition of new models to the database has an extremely weak connection with machine learning ... But the term is very painful :)

Now our task is to choose the most “close” model for a certain set of mfcc coefficients (recognizable word). At first glance, the problem can be solved quite simply:



However, the same word can be pronounced both by Andrey Malakhov and some of his Estonian colleagues. In other words, the size of the mfcc vector for the same word may be different.

Fortunately, the task of comparing sequences of different lengths has already been solved in the form of the Dynamic Time Warping algorithm. This dynamic programming algorithm is beautifully painted both in the bourgeois Wiki and in the Orthodox Habré .

The only change that should be made to it is the method of finding the distance. We have to remember that the mfcc-vector of the model is actually a sequence of mfcc- “subvectors” of dimension M, obtained from frames. So, the DTW algorithm should find the distance between the sequences of these same “subvectors” of dimension M. That is, the distances (Euclidean) between mfcc- “subvectors” of frames should be used as the values ​​of the distance matrix.

An example .



Experiments



I did not have the opportunity to test the work of this approach on a large “training” sample. The results of tests on a sample of 3 specimens for each word in non-synthetic conditions showed, to say the least, the best result - 65% of correct recognitions.

Nevertheless, my task was to create a maximum simple speech recognition application. So say “proof of concept” :)



Implementation



The attentive reader noted that the article contains many links to the GitHub project. It is worth noting here that this is my first C ++ project since university. This is also my first attempt to calculate something more complicated than the arithmetic mean since the same university ... In other words, it comes with absolutely no warranty (c) :)


Source: https://habr.com/ru/post/226143/

More articles:


All Articles