Algorithm for finding the smallest covering capacity of a finite set of its subsets
When examining old papers, I came across a fairly shabby notebook, in which I found sketches of a coating search algorithm. The author of the algorithm, Viktor Anatolyevich Shcherbanov, is my teacher, under whose guidance I worked in the nineties of the last century. My humble participation mainly consisted in the fact that I offered in most cases incorrect (and sometimes just delusional) options. What, in general, did not prevent the Chief (as we called him among themselves) did bring the work on the algorithm to its logical conclusion. Somewhere in the two thousand years, the algorithm was published in one of the institute editions of Tomsk. But I think that it will not be superfluous to remember him again. Actually, in memory of the Chef, I decided to write this post. Maybe the algorithm will seem interesting to someone or push for some new ideas on the implementation of the algorithm.
The algorithm itself is based on two statements and two theorems, the proofs of which are not given here, because of their rather large volume.
To begin with, let's define what we are actually looking for.
')
Let be a finite set and family
and family  its subsets
its subsets  .
.
Find subfamily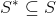 (if it exists) such that
(if it exists) such that  and the cardinality of the subfamily S * (cover of the set V) is the smallest of all possible.
and the cardinality of the subfamily S * (cover of the set V) is the smallest of all possible.
The following statements define the concepts of minimum and minimum coverage.
Statement 1.
In order for the subfamily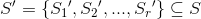 was a covering of a multitude
was a covering of a multitude  , it is necessary and sufficient that the condition be fulfilled
, it is necessary and sufficient that the condition be fulfilled
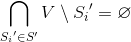
A covering S ′ is called minimal if there is no covering S ″ such that .
.
The coverage S * is called the smallest if for any minimal coverage S 'the condition
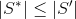
Statement 2.
Coating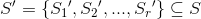 minimal if and only if for any
minimal if and only if for any  condition is met
condition is met
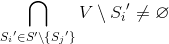
And the most basic.
Let be a finite set and family
and family  its subsets
its subsets  .
.
Construct a full loaded graph.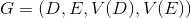 in which the set
in which the set 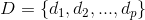 the vertices of the graph are one-to-one mapped family
the vertices of the graph are one-to-one mapped family 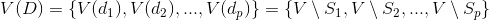 subsets
subsets  ,
,
and each edge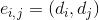 - subset
- subset  .
.
Denote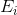 the set of all edges incident to the top
the set of all edges incident to the top 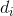 , but
, but 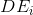 - the set of all vertices incident to the edges of the set
- the set of all vertices incident to the edges of the set 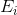 .
.
Theorem 1.
Minimum Power Subset edges incident to arbitrary vertex
edges incident to arbitrary vertex 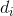 in column G, under the conditions
in column G, under the conditions
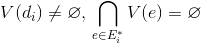
determines the minimum coverage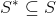 uniquely corresponding to the set
uniquely corresponding to the set 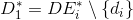 vertices if
vertices if 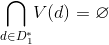 or set
or set 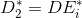 vertices if
vertices if 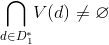 .
.
Theorem 2.
Minimum Power Subset edges incident to arbitrary vertex
edges incident to arbitrary vertex 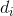 ribs
ribs 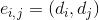 in column G, under the conditions
in column G, under the conditions
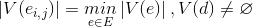 for all
for all 
determines the smallest coverage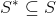 uniquely corresponding to the set
uniquely corresponding to the set 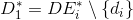 vertices if
vertices if 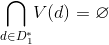 or set
or set 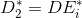 vertices if
vertices if 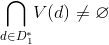 .
.
Based on the theorems, we propose the following algorithm for finding the smallest coverage.
1. Many and family
and family  its subsets
its subsets  match family
match family 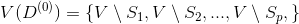 subsets
subsets 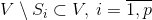 . If for some
. If for some 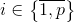 will turn out
will turn out 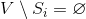 then there is a trivial covering
then there is a trivial covering 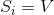 . The end of the algorithm.
. The end of the algorithm.
Otherwise, go to step 2.
2. Build a full loaded graph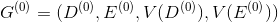 where
where 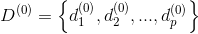 .
.
Top of load with set
load with set 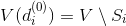
Edge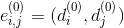 load with set
load with set 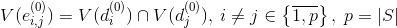 .
.
3. Check the existence of a coverage: for an arbitrary vertex define subset
define subset
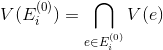 ,
,
Where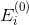 - the set of edges incident to the top
- the set of edges incident to the top  in the graph
in the graph 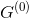 .
.
If a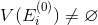 then the cover does not exist. The end of the algorithm.
then the cover does not exist. The end of the algorithm.
If a then the cover exists. Go to the procedure for finding the smallest coverage (p. 4).
then the cover exists. Go to the procedure for finding the smallest coverage (p. 4).
4. Put t: = 0.
5. In the full loaded graph find edge
find edge 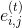 for which the condition is met
for which the condition is met 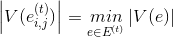 .
.
If a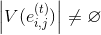 then go to step 6,
then go to step 6,
otherwise, the procedure for constructing the set D of vertices defining the smallest coverage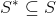 (paragraph 7).
(paragraph 7).
6. Build a full loaded graph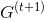 believing
believing  ,
, 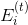 - the set of edges incident to the top
- the set of edges incident to the top 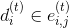 in the graph
in the graph  .
.
Put for all
for all  .
.
Put t: = t + 1 and go to step 5.
7. Start building a set of D vertices defining the smallest coverage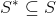 .
.
Put .
.
8. If t = 0, then go to step 11, otherwise, put t: = t-1.
9. In the column define subset
define subset 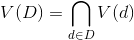
10. If in the column condition is met
condition is met 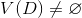 then put
then put 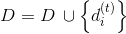 otherwise - D: = D. Go to paragraph 8.
otherwise - D: = D. Go to paragraph 8.
11. Family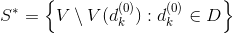 subsets
subsets 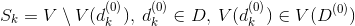 determines the smallest coverage of sets
determines the smallest coverage of sets  .
.
The end of the algorithm.
Let's try to estimate the complexity of the algorithm.
The whole, so to speak, essence of the algorithm (from the point of view of complexity estimation) lies in the phrase “we construct a complete loaded graph”.
We need to perform n actions to calculate the load at the n vertices of the graph and (n-1) n / 2 calculations (based on the number of edges of the full graph) for the load of the edges of the graph. And all this, if we consider the worst case, when the subsets do not intersect each other, is performed n-2 times. Thus, the rough estimate is O (n) = n 3 + n 2 .
In conclusion. I'm not sure that the post deserves an invite, because my involvement in the algorithm is more than dubious. But the publication, it seems to me, is worth it. I hope the moderators will understand.
How did the Greeks say? - Faisse que dois adviegne que peut (do what you must, and come what may).
(or were they Romans?)
The algorithm itself is based on two statements and two theorems, the proofs of which are not given here, because of their rather large volume.
To begin with, let's define what we are actually looking for.
')
Let be a finite set
 and family
and family  its subsets
its subsets  .
.Find subfamily
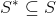 (if it exists) such that
(if it exists) such that  and the cardinality of the subfamily S * (cover of the set V) is the smallest of all possible.
and the cardinality of the subfamily S * (cover of the set V) is the smallest of all possible.The following statements define the concepts of minimum and minimum coverage.
Statement 1.
In order for the subfamily
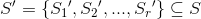 was a covering of a multitude
was a covering of a multitude  , it is necessary and sufficient that the condition be fulfilled
, it is necessary and sufficient that the condition be fulfilled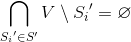
A covering S ′ is called minimal if there is no covering S ″ such that
 .
.The coverage S * is called the smallest if for any minimal coverage S 'the condition
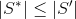
Statement 2.
Coating
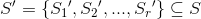 minimal if and only if for any
minimal if and only if for any  condition is met
condition is met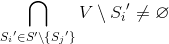
And the most basic.
Let be a finite set
 and family
and family  its subsets
its subsets  .
.Construct a full loaded graph.
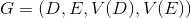 in which the set
in which the set 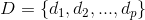 the vertices of the graph are one-to-one mapped family
the vertices of the graph are one-to-one mapped family 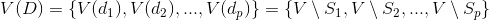 subsets
subsets  ,
,and each edge
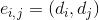 - subset
- subset  .
.Denote
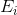 the set of all edges incident to the top
the set of all edges incident to the top 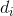 , but
, but 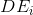 - the set of all vertices incident to the edges of the set
- the set of all vertices incident to the edges of the set 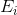 .
.Theorem 1.
Minimum Power Subset
 edges incident to arbitrary vertex
edges incident to arbitrary vertex 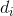 in column G, under the conditions
in column G, under the conditions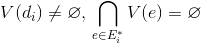
determines the minimum coverage
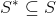 uniquely corresponding to the set
uniquely corresponding to the set 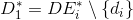 vertices if
vertices if 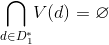 or set
or set 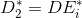 vertices if
vertices if 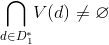 .
.Theorem 2.
Minimum Power Subset
 edges incident to arbitrary vertex
edges incident to arbitrary vertex 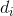 ribs
ribs 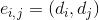 in column G, under the conditions
in column G, under the conditions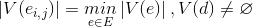 for all
for all 
determines the smallest coverage
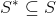 uniquely corresponding to the set
uniquely corresponding to the set 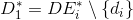 vertices if
vertices if 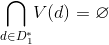 or set
or set 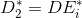 vertices if
vertices if 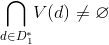 .
.Based on the theorems, we propose the following algorithm for finding the smallest coverage.
1. Many
 and family
and family  its subsets
its subsets  match family
match family 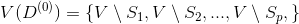 subsets
subsets 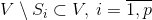 . If for some
. If for some 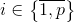 will turn out
will turn out 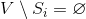 then there is a trivial covering
then there is a trivial covering 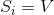 . The end of the algorithm.
. The end of the algorithm.Otherwise, go to step 2.
2. Build a full loaded graph
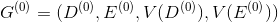 where
where 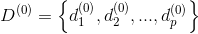 .
.Top of
 load with set
load with set 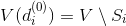
Edge
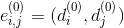 load with set
load with set 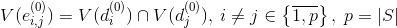 .
.3. Check the existence of a coverage: for an arbitrary vertex
 define subset
define subset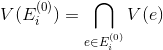 ,
,Where
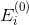 - the set of edges incident to the top
- the set of edges incident to the top  in the graph
in the graph 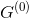 .
.If a
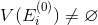 then the cover does not exist. The end of the algorithm.
then the cover does not exist. The end of the algorithm.If a
 then the cover exists. Go to the procedure for finding the smallest coverage (p. 4).
then the cover exists. Go to the procedure for finding the smallest coverage (p. 4).4. Put t: = 0.
5. In the full loaded graph
 find edge
find edge 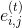 for which the condition is met
for which the condition is met 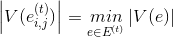 .
.If a
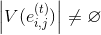 then go to step 6,
then go to step 6,otherwise, the procedure for constructing the set D of vertices defining the smallest coverage
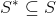 (paragraph 7).
(paragraph 7).6. Build a full loaded graph
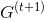 believing
believing  ,
, 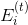 - the set of edges incident to the top
- the set of edges incident to the top 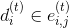 in the graph
in the graph  .
.Put
 for all
for all  .
.Put t: = t + 1 and go to step 5.
7. Start building a set of D vertices defining the smallest coverage
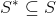 .
.Put
 .
.8. If t = 0, then go to step 11, otherwise, put t: = t-1.
9. In the column
 define subset
define subset 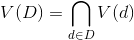
10. If in the column
 condition is met
condition is met 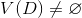 then put
then put 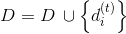 otherwise - D: = D. Go to paragraph 8.
otherwise - D: = D. Go to paragraph 8.11. Family
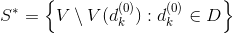 subsets
subsets 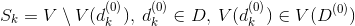 determines the smallest coverage of sets
determines the smallest coverage of sets  .
.The end of the algorithm.
Let's try to estimate the complexity of the algorithm.
The whole, so to speak, essence of the algorithm (from the point of view of complexity estimation) lies in the phrase “we construct a complete loaded graph”.
We need to perform n actions to calculate the load at the n vertices of the graph and (n-1) n / 2 calculations (based on the number of edges of the full graph) for the load of the edges of the graph. And all this, if we consider the worst case, when the subsets do not intersect each other, is performed n-2 times. Thus, the rough estimate is O (n) = n 3 + n 2 .
In conclusion. I'm not sure that the post deserves an invite, because my involvement in the algorithm is more than dubious. But the publication, it seems to me, is worth it. I hope the moderators will understand.
How did the Greeks say? - Faisse que dois adviegne que peut (do what you must, and come what may).
(or were they Romans?)
Source: https://habr.com/ru/post/225831/
All Articles