An experiment that forever changed our view of reality
The uncertainty principle says that we cannot know certain properties of a quantum system at the same moment in time. For example, we cannot simultaneously know the position of a particle and its velocity. But what does this tell us about the real world? If we could look behind the scenes of quantum theory, would we find out that objects really have a certain position and speed? Or the uncertainty principle means that at the fundamental level, objects simply do not have a clear coordinate and momentum at the same time . In other words, is our theory incomplete or reality “blurred” in reality?

The first perspective is that the use of quantum mechanics is like wearing muddy glasses. If we could somehow remove these glasses and look behind the scenes at the fundamental reality, then, of course, the particle must have some definite coordinate and momentum. After all, this is a thing in our Universe and the Universe must know where this thing is and in which direction it moves, even if we do not know it. According to this point of view, quantum mechanics is not a complete description of reality - we explore the whole subtlety of nature with a blunt instrument and therefore undoubtedly omit some details.
')
This corresponds to how everything else in our world works. When I take off my shoes and you see that I put on the red socks, you do not think that my socks were in a state of uncertain color, until we watched them, with the chance that they could be blue, yellow or pink. Instead, you (correctly) assume that my socks were always red. So why should particles work differently? Obviously, the properties of things in nature should exist regardless of whether we measure them, right?

On the other hand, it may turn out that our glasses are completely clear, but the reality is blurred. According to this view, quantum mechanics is a complete description of reality at this level and all objects in the Universe simply do not have a certain position and momentum. This is an opinion that most quantum physicists hold. These are not stupid tools, but reality is foggy in its essence. Unlike the case with my red socks, when you measure the position of a particle, it does not have a definite position until you measured it. The act of measuring the position forces the particle to have a specific position.
Now you might think that this is one of those "if-tree-falls-in-the-woods" metaphysical questions that may not have a definite answer. However, unlike most philosophical questions, there is an actual experiment that you can do to resolve this dispute. Moreover, this experiment has been done many times. In my opinion, this is one of the most undervalued ideas in our understanding of physics. The experiment is quite simple and extremely deep, because it explains something amazing about the nature of reality.
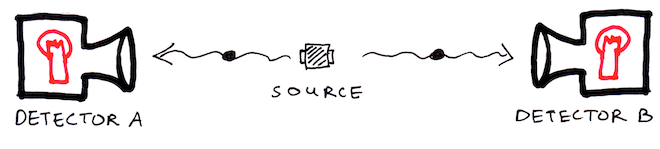
Here is the installation. There is a light source in the middle of the room. Every minute he sends two photons in opposite directions. These pairs of photons are created in a special state, known as quantum entanglement. This means that they are both connected in a quantum way - if you make measurements of one photon, you do not just change its quantum state, but immediately affect the quantum state of another photon.
On the left and right in this room are two identical boxes intended for receiving photons. Each box has an indicator light. Each time a photon enters the device, the indicator flashes in one of two colors - red or green. Each time the color of the light bulb turns out to be random - without any regularity. Apparently this box measures some property of the photon.
You can only guess what color will light up next. But the really strange thing is that whenever one box flashes in a certain color, the other box flashes the same. No matter how far you try to move the boxes away from the detector, even if they were at opposite ends of our solar system, they will blink in the same color without crashing.
It is as if these boxes were conspiring to give the same result. How is this possible? (If you have your own theory of how these boxes work, hold onto it and you will soon be able to compare your idea with experiment.)

“Aha! - the quantum enthusiast will say. - I can explain what is happening here. Each time a photon hits one of the boxes, the device measures its quantum state, which is indicated by flashing red or green. But two photons are quantum coupled, so when we measure that one photon is, say, in the “red state”, we force the other photon to be in the same state! That is why two boxes always blink in the same color. ”

“Wait a minute,” says the classical physicist. - Particles are billiard balls, not voodoo dolls. It is absurd that measuring in one place space can instantly affect something in a completely different place. When I notice that one of my socks is red, it does not change the condition of my other sock, causing it to be red too. The simple explanation is that the photons in this experiment, like socks, are created in pairs. Sometimes they are both in the red state, in other cases - in the green. These boxes simply measure the hidden parameters of the photons.
The experiment and the arguments presented here are a version of a mental experiment, first formulated by Einstein, Podolsky and Rosen, and is known as the EPR paradox . The crucial point of their argument is that it seems absurd that the measurement in one place can instantly affect the measurement in a completely different place. A more logical explanation is that the boxes detect some hidden properties that both photons possess. From the moment of their creation, these photons have some kind of hidden stamp, like a passport, which relates them to a red or green state. Boxes must define this stamp. Einstein, Podolsky and Rosen argued that the randomness that we observe in these experiments is our gap in the theory of nature. According to them - our glasses are muddy. In the terminology of field theories, this idea is known as The Theory of Hidden Parameters .

It would seem that classical physics won this round, with the explanation that it is simpler and more meaningful.
The next day, a new pair of boxes comes in the mail. The new version of the box has three built-in doors. You can only open one door at a time. Behind each door an indicator that, as before, can glow red or green.

Both physics are played with these new devices, catching photons and watching what happens when they open the doors. After a few hours of fuss, they find out:
1. If they open the same door on both boxes, the bulbs always light in the same color.
2. If they open the doors of two boxes at random, the same color appears exactly half the time.
After some thought, the classical physicist comes up with a simple explanation for this experiment. “In principle, this is not very different from yesterday’s boxes. This can be explained as follows. Suppose that instead of a single stamp, each photon from a pair now has three stamps, like the presence of several passports. Each door of the box corresponds to one of these stamps. For example, three stamps can be red, green, red. This will mean that the indicator behind the first door will flash red, the second green and the third red too. ”
“This idea explains that when we open the same door on both boxes, we get the same color, because both boxes read the same stamp. But when we open different doors, the devices read different stamps, so they can produce different results. ”
And again the explanation of classical physics is simple and does not concern any fashionable concepts, like quantum entanglement or uncertainty principle.
“Not so fast,” says a quantum physicist, who has just finished writing a calculation in his notebook. “When we open doors at random, we find that the lights blink half the same time in the same color. This number - 0.5 - exactly coincides with the predictions of quantum mechanics. But according to your “theory of hidden parameters,” the lights should flash more than half the same color! ”
“According to the idea of hidden parameters, there are 8 possible combinations of stamps that photons can have. Let's call them by the first letters of the colors for short, so RRG = red, red, green. ”
“Now, if we choose doors randomly, then in a third of cases we will choose the same door and see the same color.”
“The remaining two thirds of the time, we choose different doors. Let's say we deal with photons with the following configuration of stamps ":
“In this configuration, if we chose door 1 on one box and door 2 on the other, the indicators glow in the same colors (red and red). But if we chose doors 1 and 3 or doors 2 and 3, the colors are different (red and green). Thus, in one third of such cases, the boxes give the same color. ”
"Summarizing. In a third of the cases, the boxes have the same color, because we chose the same doors. Two thirds of the time we choose different doors, and in one third of these cases we will get the same color. ”
"Calculate":
⅓ + ⅔ ⅓ = 3/9 + 2/9 = 5/9 = 55.55%
“55.55% is the probability that the boxes will light up in the same color when we choose two doors at random, in accordance with the theory of hidden parameters.”
“But wait! We dismantled only one combination - RRG. But what about the rest? Looking quickly, you will notice that mathematics remains exactly the same in all the following cases ”:
"There are two options":
“In these situations we will get the same colors no matter which door we choose.” Thus, the chances of choosing the same color only increase . ”
“The culmination is that, according to the idea of hidden parameters, the chances of the boxes to flash in the same color when we open the doors at random are at least 55.55%. But according to quantum mechanics, the answer is 50%. Experimental data are consistent with quantum mechanics, and this excludes the theory of hidden parameters. ”
You can pause and think what we just showed.
We looked at a pioneering argument in quantum mechanics, known as Bell's Theorem . The black boxes do not actually blink with red and green lights, but the key details coincide with actual experiments that measure the polarization of tangled photons.
Bell's theorem draws a line in the sand between the strange quantum world and the classical world that we know and love. This proves that theories of hidden parameters and similar theories that Einstein and his friends invented do not reflect the real world. Instead, quantum mechanics appears with its particles, which can be linked at large distances. When you perturb the quantum state of one of these entangled particles, you instantly perturb the state of another, no matter where it is in the Universe.
It is gratifying to think that we could explain the strangeness of quantum mechanics if we imagined everyday particles with small invisible mechanisms inside or invisible stamps, or hidden notebooks, or something else — some hidden variables that we do not have access to and which "Real" coordinates and momentum, and other details about the particle. It is comfortable to think that at a fundamental level, reality behaves classically and that our clumsy theory does not allow us to look into this hidden register. But Bell's Theorem deprives us of this comfort. The reality is blurred , and we just have to get used to this fact.


Option 1: Muddy glasses, clear reality
The first perspective is that the use of quantum mechanics is like wearing muddy glasses. If we could somehow remove these glasses and look behind the scenes at the fundamental reality, then, of course, the particle must have some definite coordinate and momentum. After all, this is a thing in our Universe and the Universe must know where this thing is and in which direction it moves, even if we do not know it. According to this point of view, quantum mechanics is not a complete description of reality - we explore the whole subtlety of nature with a blunt instrument and therefore undoubtedly omit some details.
')
This corresponds to how everything else in our world works. When I take off my shoes and you see that I put on the red socks, you do not think that my socks were in a state of uncertain color, until we watched them, with the chance that they could be blue, yellow or pink. Instead, you (correctly) assume that my socks were always red. So why should particles work differently? Obviously, the properties of things in nature should exist regardless of whether we measure them, right?

Option 2: Clear points, muddy reality
On the other hand, it may turn out that our glasses are completely clear, but the reality is blurred. According to this view, quantum mechanics is a complete description of reality at this level and all objects in the Universe simply do not have a certain position and momentum. This is an opinion that most quantum physicists hold. These are not stupid tools, but reality is foggy in its essence. Unlike the case with my red socks, when you measure the position of a particle, it does not have a definite position until you measured it. The act of measuring the position forces the particle to have a specific position.
Now you might think that this is one of those "if-tree-falls-in-the-woods" metaphysical questions that may not have a definite answer. However, unlike most philosophical questions, there is an actual experiment that you can do to resolve this dispute. Moreover, this experiment has been done many times. In my opinion, this is one of the most undervalued ideas in our understanding of physics. The experiment is quite simple and extremely deep, because it explains something amazing about the nature of reality.

Here is the installation. There is a light source in the middle of the room. Every minute he sends two photons in opposite directions. These pairs of photons are created in a special state, known as quantum entanglement. This means that they are both connected in a quantum way - if you make measurements of one photon, you do not just change its quantum state, but immediately affect the quantum state of another photon.
On the left and right in this room are two identical boxes intended for receiving photons. Each box has an indicator light. Each time a photon enters the device, the indicator flashes in one of two colors - red or green. Each time the color of the light bulb turns out to be random - without any regularity. Apparently this box measures some property of the photon.
You can only guess what color will light up next. But the really strange thing is that whenever one box flashes in a certain color, the other box flashes the same. No matter how far you try to move the boxes away from the detector, even if they were at opposite ends of our solar system, they will blink in the same color without crashing.
It is as if these boxes were conspiring to give the same result. How is this possible? (If you have your own theory of how these boxes work, hold onto it and you will soon be able to compare your idea with experiment.)

“Aha! - the quantum enthusiast will say. - I can explain what is happening here. Each time a photon hits one of the boxes, the device measures its quantum state, which is indicated by flashing red or green. But two photons are quantum coupled, so when we measure that one photon is, say, in the “red state”, we force the other photon to be in the same state! That is why two boxes always blink in the same color. ”

“Wait a minute,” says the classical physicist. - Particles are billiard balls, not voodoo dolls. It is absurd that measuring in one place space can instantly affect something in a completely different place. When I notice that one of my socks is red, it does not change the condition of my other sock, causing it to be red too. The simple explanation is that the photons in this experiment, like socks, are created in pairs. Sometimes they are both in the red state, in other cases - in the green. These boxes simply measure the hidden parameters of the photons.
The experiment and the arguments presented here are a version of a mental experiment, first formulated by Einstein, Podolsky and Rosen, and is known as the EPR paradox . The crucial point of their argument is that it seems absurd that the measurement in one place can instantly affect the measurement in a completely different place. A more logical explanation is that the boxes detect some hidden properties that both photons possess. From the moment of their creation, these photons have some kind of hidden stamp, like a passport, which relates them to a red or green state. Boxes must define this stamp. Einstein, Podolsky and Rosen argued that the randomness that we observe in these experiments is our gap in the theory of nature. According to them - our glasses are muddy. In the terminology of field theories, this idea is known as The Theory of Hidden Parameters .

It would seem that classical physics won this round, with the explanation that it is simpler and more meaningful.
The next day, a new pair of boxes comes in the mail. The new version of the box has three built-in doors. You can only open one door at a time. Behind each door an indicator that, as before, can glow red or green.

Both physics are played with these new devices, catching photons and watching what happens when they open the doors. After a few hours of fuss, they find out:
1. If they open the same door on both boxes, the bulbs always light in the same color.
2. If they open the doors of two boxes at random, the same color appears exactly half the time.
After some thought, the classical physicist comes up with a simple explanation for this experiment. “In principle, this is not very different from yesterday’s boxes. This can be explained as follows. Suppose that instead of a single stamp, each photon from a pair now has three stamps, like the presence of several passports. Each door of the box corresponds to one of these stamps. For example, three stamps can be red, green, red. This will mean that the indicator behind the first door will flash red, the second green and the third red too. ”
“This idea explains that when we open the same door on both boxes, we get the same color, because both boxes read the same stamp. But when we open different doors, the devices read different stamps, so they can produce different results. ”
And again the explanation of classical physics is simple and does not concern any fashionable concepts, like quantum entanglement or uncertainty principle.
“Not so fast,” says a quantum physicist, who has just finished writing a calculation in his notebook. “When we open doors at random, we find that the lights blink half the same time in the same color. This number - 0.5 - exactly coincides with the predictions of quantum mechanics. But according to your “theory of hidden parameters,” the lights should flash more than half the same color! ”
“According to the idea of hidden parameters, there are 8 possible combinations of stamps that photons can have. Let's call them by the first letters of the colors for short, so RRG = red, red, green. ”
Rrg
Rgr
GRR
Ggr
GRG
Rgg
RRR
GGG
“Now, if we choose doors randomly, then in a third of cases we will choose the same door and see the same color.”
“The remaining two thirds of the time, we choose different doors. Let's say we deal with photons with the following configuration of stamps ":
Rrg
“In this configuration, if we chose door 1 on one box and door 2 on the other, the indicators glow in the same colors (red and red). But if we chose doors 1 and 3 or doors 2 and 3, the colors are different (red and green). Thus, in one third of such cases, the boxes give the same color. ”
"Summarizing. In a third of the cases, the boxes have the same color, because we chose the same doors. Two thirds of the time we choose different doors, and in one third of these cases we will get the same color. ”
"Calculate":
⅓ + ⅔ ⅓ = 3/9 + 2/9 = 5/9 = 55.55%
“55.55% is the probability that the boxes will light up in the same color when we choose two doors at random, in accordance with the theory of hidden parameters.”
“But wait! We dismantled only one combination - RRG. But what about the rest? Looking quickly, you will notice that mathematics remains exactly the same in all the following cases ”:
Rrg
Rgr
GRR
Ggr
GRG
Rgg
"There are two options":
RRR
GGG
“In these situations we will get the same colors no matter which door we choose.” Thus, the chances of choosing the same color only increase . ”
“The culmination is that, according to the idea of hidden parameters, the chances of the boxes to flash in the same color when we open the doors at random are at least 55.55%. But according to quantum mechanics, the answer is 50%. Experimental data are consistent with quantum mechanics, and this excludes the theory of hidden parameters. ”
You can pause and think what we just showed.
We looked at a pioneering argument in quantum mechanics, known as Bell's Theorem . The black boxes do not actually blink with red and green lights, but the key details coincide with actual experiments that measure the polarization of tangled photons.
Bell's theorem draws a line in the sand between the strange quantum world and the classical world that we know and love. This proves that theories of hidden parameters and similar theories that Einstein and his friends invented do not reflect the real world. Instead, quantum mechanics appears with its particles, which can be linked at large distances. When you perturb the quantum state of one of these entangled particles, you instantly perturb the state of another, no matter where it is in the Universe.
It is gratifying to think that we could explain the strangeness of quantum mechanics if we imagined everyday particles with small invisible mechanisms inside or invisible stamps, or hidden notebooks, or something else — some hidden variables that we do not have access to and which "Real" coordinates and momentum, and other details about the particle. It is comfortable to think that at a fundamental level, reality behaves classically and that our clumsy theory does not allow us to look into this hidden register. But Bell's Theorem deprives us of this comfort. The reality is blurred , and we just have to get used to this fact.

Source: https://habr.com/ru/post/225583/
All Articles