Cellular automata with komonad
One evening I came across an article on the implementation of a one-dimensional cellular automaton using komonads, but the material is incomplete and a bit outdated, and therefore decided to write a Russian-language adaptation (at the same time having considered two-dimensional cellular automata on the example of Game of Life):
Consider the data type
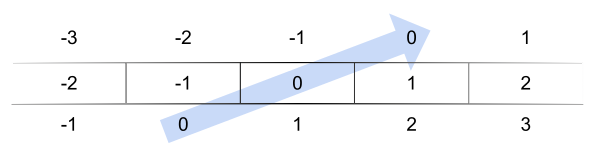
This is an endless list on both sides, but with a focus on a certain element that we can shift using functions:
')
In essence, this is a type of fastener ( zipper ), but we can regard it as a constant C-pointer to an infinite memory area: the increment and decrement operations apply to it. But how to dereference it? To do this, we define a function that has a focused value:
For example,

If we want to get all degrees 2, we need a way to apply the function
In the cellular automaton, the values of the cells depend on the values of all the other cells in the previous step. Therefore, we can create the
The convolution rule must be of the type
Applying the rule to the Universe of all shifts, we obtain the following state of the automaton:

We can notice that our functions are subject to the following laws:
Therefore, the
Now, we can equally well realize a two-dimensional cellular automaton. First, let's declare the type of two-dimensional
In Haskell, it is very easy to apply a function to nested containers using
An instance of a comonad is done in the same way as a regular Universe, and since Universe2 is only a wrapper, we can define methods in terms of those already available. For example,
This is almost everything! It remains only to define the rule and apply it with
Here is the rule itself:
There remains only a boring conclusion, which I will not consider separately.
Thus, we can implement any cellular automaton, just by defining the
The fact is that since we apply the rule to each element of the infinite list, it will be necessary to go through all the previous steps to compute the cells to which there has not yet been any appeal, which means they need to be stored in memory.
Source codes of both files:
Thanks int_index for help in preparing the article.
Universe
Consider the data type
Universe , defined as follows: data Universe a = Universe [a] a [a] This is an endless list on both sides, but with a focus on a certain element that we can shift using functions:
')
left, right :: Universe a -> Universe a left (Universe (a:as) x bs) = Universe as a (x:bs) right (Universe as x (b:bs)) = Universe (x:as) b bs In essence, this is a type of fastener ( zipper ), but we can regard it as a constant C-pointer to an infinite memory area: the increment and decrement operations apply to it. But how to dereference it? To do this, we define a function that has a focused value:
extract :: Universe a -> a extract (Universe _ x _) = x For example,
Universe [-1, -2..] 0 [1, 2..] is all integers. However, Universe [0, -1..] 1 [2, 3..] are the same integers, but with a slightly changed context (we point to another element).
If we want to get all degrees 2, we need a way to apply the function
(2**) to the Universe integers. It is easy to define an instance of the class Functor, which obeys all laws: instance Functor Universe where fmap f (Universe as x bs) = Universe (fmap f as) (fx) (fmap f bs) -- powersOf2 = fmap (2**) (Universe [-1, -2..] 0 [1, 2..]) -- ..0.25, 0.5, 1, 2, 4.. In the cellular automaton, the values of the cells depend on the values of all the other cells in the previous step. Therefore, we can create the
Universe all shifts and the rule of their convolution: duplicate :: Universe a -> Universe (Universe a) duplicate u = Universe (tail $ iterate left u) u (tail $ iterate right u) 
The convolution rule must be of the type
Universe a -> a , so for the Universe Bool an example of a rule might be: rule :: Universe Bool -> Bool rule u = lx /= cx where lx = extract $ left u cx = extract u Applying the rule to the Universe of all shifts, we obtain the following state of the automaton:
next :: Universe a -> (Universe a -> a) -> Universe a next ur = fmap r (duplicate u) -- un = Universe (repeat False) True (repeat False) `next` rule 
Komonad
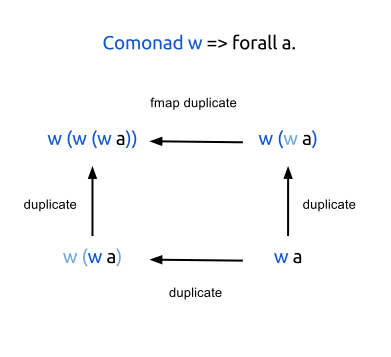
We can notice that our functions are subject to the following laws:
extract . duplicate = id fmap extract . duplicate = id duplicate . duplicate = fmap duplicate . duplicate Therefore, the
Universe forms a comonad , and the next function corresponds to the operator (=>>) . Komonada is a dual monad, in connection with which one can trace some analogies between their operations. For example, join combines nested contexts, and duplicate , on the contrary, doubles the context; return puts context, extract extracts from it, etc.
Two-dimensional cellular automaton
Now, we can equally well realize a two-dimensional cellular automaton. First, let's declare the type of two-dimensional
Universe : newtype Universe2 a = Universe2 { getUniverse2 :: Universe (Universe a) } In Haskell, it is very easy to apply a function to nested containers using
fmap composition, so writing an instance of the Functor class for Universe2 will be no problem: instance Functor Universe2 where fmap f = Universe2 . (fmap . fmap) f . getUniverse2 An instance of a comonad is done in the same way as a regular Universe, and since Universe2 is only a wrapper, we can define methods in terms of those already available. For example,
extract simply enough to run twice. In duplicate , however, we have to receive shifts of nested contexts, for which an auxiliary function is defined. instance Comonad Universe2 where extract = extract . extract . getUniverse2 duplicate = fmap Universe2 . Universe2 . shifted . shifted . getUniverse2 where shifted :: Universe (Universe a) -> Universe (Universe (Universe a)) shifted u = Universe (tail $ iterate (fmap left) u) u (tail $ iterate (fmap right) u) This is almost everything! It remains only to define the rule and apply it with
(=>>) . In Game of Life, a new state of a cell depends on the state of neighboring cells, so we define the function of their location: nearest3 :: Universe a -> [a] nearest3 u = fmap extract [left u, u, right u] neighbours :: (Universe2 a) -> [a] neighbours u = [ nearest3 . extract . left , pure . extract . left . extract , pure . extract . right . extract , nearest3 . extract . right ] >>= ($ getUniverse2 u) Here is the rule itself:
data Cell = Dead | Alive deriving (Eq, Show) rule :: Universe2 Cell -> Cell rule u | nc == 2 = extract u | nc == 3 = Alive | otherwise = Dead where nc = length $ filter (==Alive) (neighbours u) There remains only a boring conclusion, which I will not consider separately.
Conclusion
Thus, we can implement any cellular automaton, just by defining the
rule function. We get an infinite field as a gift, thanks to lazy calculations, although this creates such a problem as linear memory consumption.The fact is that since we apply the rule to each element of the infinite list, it will be necessary to go through all the previous steps to compute the cells to which there has not yet been any appeal, which means they need to be stored in memory.
Source codes of both files:
Universe.hs
module Universe where import Control.Comonad data Universe a = Universe [a] a [a] newtype Universe2 a = Universe2 { getUniverse2 :: Universe (Universe a) } left :: Universe a -> Universe a left (Universe (a:as) x bs) = Universe as a (x:bs) right :: Universe a -> Universe a right (Universe as x (b:bs)) = Universe (x:as) b bs makeUniverse fl fr x = Universe (tail $ iterate fl x) x (tail $ iterate fr x) instance Functor Universe where fmap f (Universe as x bs) = Universe (fmap f as) (fx) (fmap f bs) instance Comonad Universe where duplicate = makeUniverse left right extract (Universe _ x _) = x takeRange :: (Int, Int) -> Universe a -> [a] takeRange (a, b) u = take (b-a+1) x where Universe _ _ x | a < 0 = iterate left u !! (-a+1) | otherwise = iterate right u !! (a-1) instance Functor Universe2 where fmap f = Universe2 . (fmap . fmap) f . getUniverse2 instance Comonad Universe2 where extract = extract . extract . getUniverse2 duplicate = fmap Universe2 . Universe2 . shifted . shifted . getUniverse2 where shifted :: Universe (Universe a) -> Universe (Universe (Universe a)) shifted = makeUniverse (fmap left) (fmap right) takeRange2 :: (Int, Int) -> (Int, Int) -> Universe2 a -> [[a]] takeRange2 (x0, y0) (x1, y1) = takeRange (y0, y1) . fmap (takeRange (x0, x1)) . getUniverse2 Life.hs
import Control.Comonad import Control.Applicative import System.Process (rawSystem) import Universe data Cell = Dead | Alive deriving (Eq, Show) nearest3 :: Universe a -> [a] nearest3 u = fmap extract [left u, u, right u] neighbours :: (Universe2 a) -> [a] neighbours u = [ nearest3 . extract . left , pure . extract . left . extract , pure . extract . right . extract , nearest3 . extract . right ] >>= ($ getUniverse2 u) rule :: Universe2 Cell -> Cell rule u | nc == 2 = extract u | nc == 3 = Alive | otherwise = Dead where nc = length $ filter (==Alive) (neighbours u) renderLife :: Universe2 Cell -> String renderLife = unlines . map concat . map (map renderCell) . takeRange2 (-7, -7) (20, 20) where renderCell Alive = "██" renderCell Dead = " " fromList :: a -> [a] -> Universe a fromList d (x:xs) = Universe (repeat d) x (xs ++ repeat d) fromList2 :: a -> [[a]] -> Universe2 a fromList2 d = Universe2 . fromList ud . fmap (fromList d) where ud = Universe (repeat d) d (repeat d) cells = [ [ Dead, Alive, Dead] , [Alive, Dead, Dead] , [Alive, Alive, Alive] ] main = do gameLoop $ fromList2 Dead cells gameLoop :: Universe2 Cell -> IO a gameLoop u = do getLine rawSystem "clear" [] putStr $ renderLife u gameLoop (u =>> rule) Thanks int_index for help in preparing the article.
Source: https://habr.com/ru/post/225473/
All Articles