One combinatorial generation algorithm
Combinatorics in high school, as a rule, is limited to word problems, in which you need to apply one of three well-known formulas - for the number of combinations, permutations or placements. The institute courses in discrete mathematics also tell about more complex combinatorial objects - bracket sequences, trees, graphs ... In this case, as a rule, they set the task to calculate the number of objects of this type for some parameter n, for example the number of trees on n vertices. Having learned the number of objects for a fixed n, one can ask a more complicated question: how can we present all these objects in a reasonable time? Algorithms that solve this kind of problem are called combinatorial generation algorithms. For example, the first chapter of the fourth volume of Donald Knuth's The Art of Programming is devoted to such algorithms. Knut very thoroughly examines the algorithms for generating all tuples, partitions of numbers, trees, and other structures. It is easy to come up with any algorithm that works moderately quickly for each of these tasks, but with further optimization serious problems may arise.
In the process of writing a master's thesis, defended at the Academic University , I needed to study and apply one of the combinatorial generation algorithms suitable for a particular class of problems. This is the generation of structures on which some equivalence relation is additionally introduced. To make it clear what is at stake, I will give a simple example. Let's try to generate all the triangulations of a hexagon. It turns out something like this:

')
To write an algorithm that returns all such triangulations is pretty easy. For example, such a procedure would fit: fix some edge (let it be edge 1-6), after which we loop through vertices that are not its ends. At the current vertex and fixed edge, we construct a triangle, and the remaining two regions after that are triangulated by recursively. If you look at the triangulations resulting from the operation of this algorithm, you can see that many of them are almost the same and differ only in how the labels (numbers) of the vertices are arranged. Therefore, it would be useful to come up with an algorithm that will generate so-called unlabeled triangulations — those shown in the following figure:

More formally, let some equivalence relation act on our set of objects, dividing the whole set into classes of objects isomorphic to each other. It is required to generate one representative from each class. You have probably noticed that the two right triangulations in the second figure are also very similar to each other and only one of them can be left. In fact, it all depends on which equivalence relation we choose. If we consider only those triangulations that can be superimposed on each other after a turn is isomorphic, then there will be four of them, and if we still allow the possibility to turn the hexagon, then three.
It would seem that it is easy to generate one representative from each class: we generate all the objects, after which we test in pairs for isomorphism and throw out duplicates. Unfortunately, for some types of objects this will work terribly long even for small n. The task of checking isomorphism, for example, two graphs, is not able to solve for polynomial time, which means that it is desirable to call the subroutine that solves this problem as little as possible. Another disadvantage of the proposed naive approach is that all objects must be kept in memory at the same time. At the same time, if you wait for a slow program that gives the right answer, you can theoretically still, then getting memory overflow instead of an answer is completely unacceptable. So, to generate pairwise non-isomorphic objects, you need to use some more cunning method. Such a method was repeatedly rediscovered for many specific combinatorial objects (graphs, trees, partitions), and in general, was described in the article Isomorph-Free Exhaustive Generation .
I will talk about this method using the example of a task that is somewhat more general than the problem of triangulations: we will generate all the “cuts”, that is, the ways to split a polygon are not necessarily triangles, but polygons with a number of sides from the list that is input the program.
In order to describe this method we need several formal definitions.
Let X be some set of “structures”. Elements of the set X will be called labeled objects . In our task, the marked objects are cuts whose vertices are numbered counterclockwise. The data structure for tagged cuts is simple - these are adjacency lists:
Let G be some permutation group acting on a set X. This means that each labeled object x from X and each element g of group G are assigned another labeled object y = g * x, and the following properties are true:
It can be shown that the whole set X is divided into equivalence classes of the relative relation: x and y are equivalent if x = g * y. In our first example with triangulations, the elements of the group — turns by 0, 60, 120, 180, 240, and 300 degrees — divide the whole set into four equivalence classes, whose elements differ precisely in their structure, and not in the marks of the vertices. These equivalence classes were depicted in the second figure. We will call these classes unlabeled objects .
To each element of X, we associate a natural number, which we will call order. The order of all equivalent objects must be the same. This property allows you to further define the order for equivalence classes (unlabeled objects): it will be equal to the order of any representative of the corresponding class. For our example in the figure, the order is the number of vertices in the polygon. All unlabeled objects in the figure are six.
These were fairly general definitions. We now turn to definitions specific to the future algorithm. To each marked object x, we associate two sets — the set of lower objects L (x) and the set of upper objects U (x). The orders of the elements in these sets are by definition equal to the order of x. Before giving formal requirements for lower and upper objects, I will try to give an intuitive description. Each lower object must contain information about how to uniquely move from the current object to an object of a smaller order. For example, a lower dissection object is a dissection in which one of the "extreme" polygons is additionally highlighted (for example, colored red), which can be cut off from this dissection. The upper object is, on the contrary, the marked object plus information, allowing it to unambiguously “increase” it by increasing the order. The upper dissection, for example, is a dissection in which one of the sides of the polygon is additionally highlighted (for example, colored red) and a number is written on it. Looking at this cut, we can figure out which side to glue the new polygon to increase the order. The number of sides of the glued polygon will be determined by what number is written on the edge. This idea can be illustrated by the following figure, depicting two objects - the lower and the upper, corresponding to the same dissection.
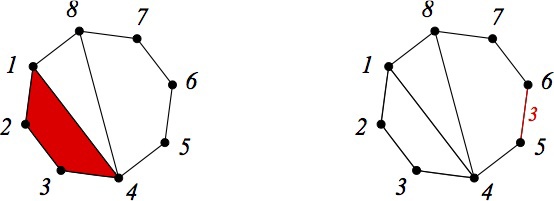
In the program, the lower and upper cuts are presented as follows:
For the lower dissection, we store only the number of the vertex from which the polygon begins, which we are going to delete. For the top cut, the number of the vertex is stored, after which it will be necessary to paste a new polygon, as well as the number of its sides.
You can see that some of the lower and upper objects are in the relation of "correspondence": the lower object corresponds to the upper one, which is obtained after we reduced the order in the manner encoded in the lower object.

Here the top object is mapped to the lower object, the result of deleting the selected quadrilateral. In the following picture - the opposite: a pentagon is glued to the top object, or rather, to its highlighted edge with the five written on it. This results in a lower object that stores information on how to roll back the operation performed.
Now, formally, what do you need to require from the mentioned structures:
To better understand this concept, I suggest you distract from reading for a moment and think about what the lower and upper objects will look like if you take graphs without triangles as X (that is, graphs in which no three vertices are connected by edges all at once ).
We continue. Let nothing can be “bitten off” from some unlabeled object. Thus, there are no lower objects corresponding to it (or rather, corresponding to its marked objects). Such an object is called irreducible . In our case, irreducible are dissections consisting of a single polygon. All others are reducible .
Our algorithm will generate all non-isomorphic cuts sequentially, starting with irreducible ones, gradually increasing their order. To do this, we will paste all possible polygons from all possible sides to the current section. The problem, however, is that one can come to the same dissection in several ways. For example, you can come to the cut of the octagon, which corresponded to the lower object in the two previous pictures, by gluing a quadrilateral to a triangle, and then a pentagon, or by gluing, on the contrary, a triangle and a quadrilateral to a pentagon. Thus, it is possible to generate the same dissection several times, and not even notice it. This is what you just want to avoid.
To get around this problem by generating a new dissection, we will check if it is true that the last addition of the polygon corresponds to some single canonical way of constructing this dissection. To do this, we need the function P, which associates with each marked object a set of lower objects for which it is a “descendant”. The function P must meet the following requirements:
It is worth paying special attention to the second requirement: it, in fact, means that the set P (x) must consist of several objects that are equivalent with respect to the symmetries of the object x. Suppose, for example, it turned out that the dissection of x is symmetrical about only turns to 0 and 180 degrees. Then P (x) must consist of exactly two lower objects, obtained from each other by means of such turns.
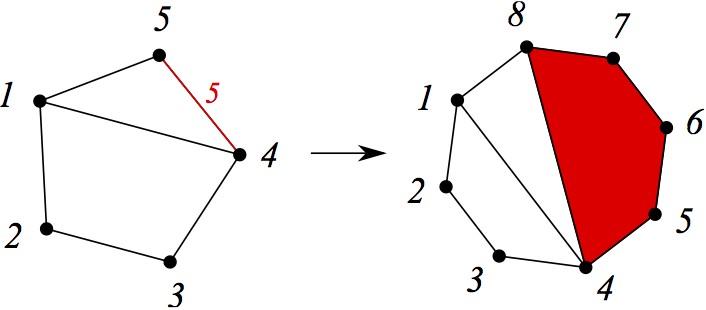
Let's try to satisfy the general requirement in our example. To do this, take some dissection x and scroll through it marks all n ways (n is the number of vertices). Every time when the “extreme” polygon starts from the vertices 1 and 2 (such that it can be cut off), we will remember this numbering. After that, from all the selected vertex numbering options, choose those that give a lexicographically minimal (any other reasonable order) the adjacency list entry. These numbering allocates us some polygons on the source object x - those that, with appropriate numbering, start with 1 and 2. P (x) just consists of lower objects for x, in which these polygons are colored red. You can't do without a picture:

So, we chose the cut x, shown on the left, and rearranged the marks in eight different ways. The methods a, c, e and g do not immediately suit us: on the vertices 1,2, ..., i, there is no polygon that can be cut off. It can be seen that methods b and f are essentially the same, as are methods d and h. Of these four methods, choose those that are in some sense "minimal." As we have already noticed, you can define at least as you like, but definitely. For example, a minimal lexicographically record of adjacency lists is appropriate. In this case, methods b and f win. This method gives us triangles 2,3,4 and 6,7,8 on the original tagged object x. As a result, we get the two lower objects shown in the figure on the right.
The P function is the most important for fast generation. To meet these requirements and maintain high speed, in fact, it is very difficult. As can be seen, the function P, in a certain sense, allows us to indicate which of the ways to “bite off” the extreme polygon is canonical, up to isomorphism. If the concept is clear, I suggest you figure out how the P (x) function should work for the already mentioned graphs without triangles.
The code that adds to the classes described above methods that implement all of these functions, it is better to look in the repository : it has too many technical details to discuss it in detail.
Now everything is ready to describe directly the generation algorithm. It will run for every irreducible cut. For the current dissection, we consider all non-isomorphic ways to create the top object, and then we increment each resulting top object to the bottom with increasing order. Further, using the P function, we check every lower object for the fact that it is indeed the parent of the corresponding marked object. If this check passes, then we consider that this tagged object is a representative of a new equivalence class; we run the algorithm for it recursively. You can, of course, prove the correctness of this algorithm, but I feel that I already overdid it a little with formalism, and in order to deal with the evidence, it is easier to refer to the original article .
Better let's look first at the code responsible for generating:
And now for the result of generating all non-isomorphic cuts into 3.4 and 5-gons, up to an order equal to eight. Arrows are directed from parents to descendants. It can be seen that all the dissections formed trees whose roots are irreducible objects.
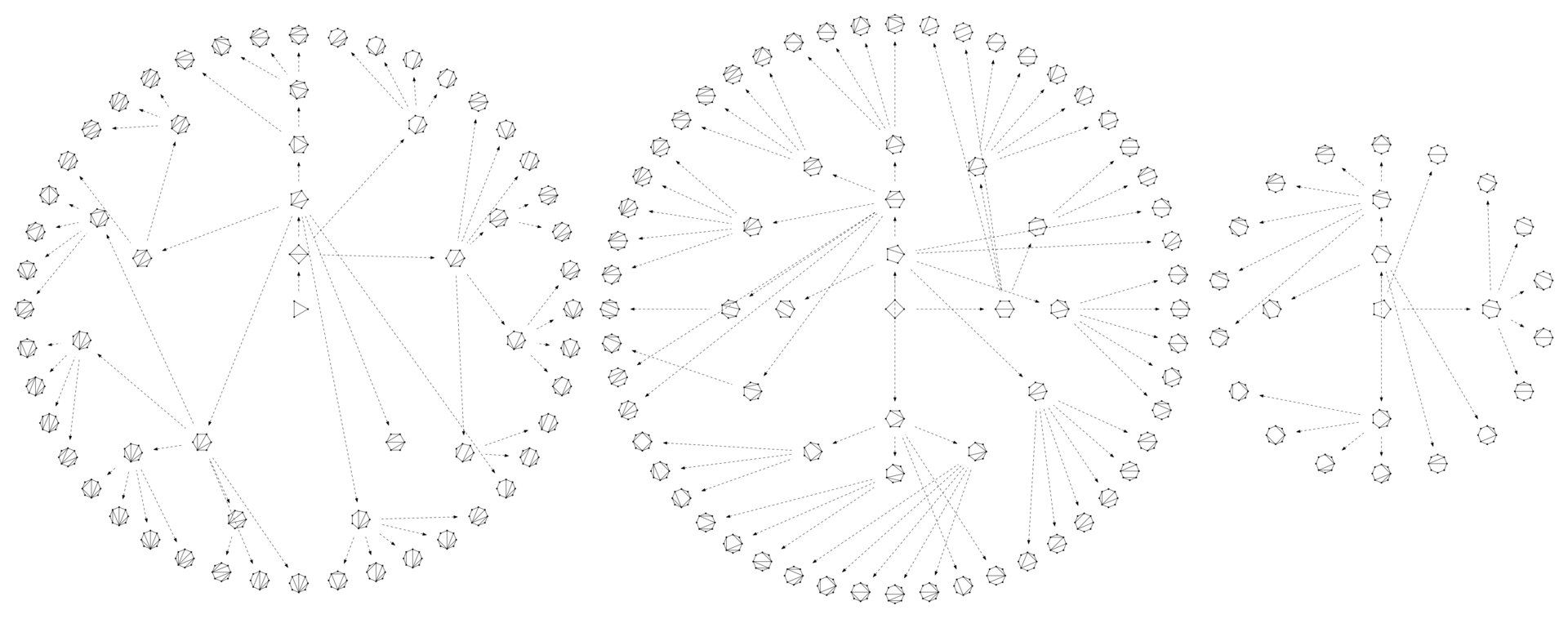
The source code of the program that generated this image is available in google code . The result of her work is a description in graphviz format.
In conclusion, I will add that for the considered problem, in principle, one can come up with a simpler and faster algorithm. However, the described procedure is applicable to almost all types of combinatorial objects that can be constructed in an inductive way, “building up” the structure. Moreover, for some types of graphs, at least, according to the author of the algorithm, this approach provides some of the best, if not the best, generation rates today.
In the process of writing a master's thesis, defended at the Academic University , I needed to study and apply one of the combinatorial generation algorithms suitable for a particular class of problems. This is the generation of structures on which some equivalence relation is additionally introduced. To make it clear what is at stake, I will give a simple example. Let's try to generate all the triangulations of a hexagon. It turns out something like this:

')
To write an algorithm that returns all such triangulations is pretty easy. For example, such a procedure would fit: fix some edge (let it be edge 1-6), after which we loop through vertices that are not its ends. At the current vertex and fixed edge, we construct a triangle, and the remaining two regions after that are triangulated by recursively. If you look at the triangulations resulting from the operation of this algorithm, you can see that many of them are almost the same and differ only in how the labels (numbers) of the vertices are arranged. Therefore, it would be useful to come up with an algorithm that will generate so-called unlabeled triangulations — those shown in the following figure:

More formally, let some equivalence relation act on our set of objects, dividing the whole set into classes of objects isomorphic to each other. It is required to generate one representative from each class. You have probably noticed that the two right triangulations in the second figure are also very similar to each other and only one of them can be left. In fact, it all depends on which equivalence relation we choose. If we consider only those triangulations that can be superimposed on each other after a turn is isomorphic, then there will be four of them, and if we still allow the possibility to turn the hexagon, then three.
It would seem that it is easy to generate one representative from each class: we generate all the objects, after which we test in pairs for isomorphism and throw out duplicates. Unfortunately, for some types of objects this will work terribly long even for small n. The task of checking isomorphism, for example, two graphs, is not able to solve for polynomial time, which means that it is desirable to call the subroutine that solves this problem as little as possible. Another disadvantage of the proposed naive approach is that all objects must be kept in memory at the same time. At the same time, if you wait for a slow program that gives the right answer, you can theoretically still, then getting memory overflow instead of an answer is completely unacceptable. So, to generate pairwise non-isomorphic objects, you need to use some more cunning method. Such a method was repeatedly rediscovered for many specific combinatorial objects (graphs, trees, partitions), and in general, was described in the article Isomorph-Free Exhaustive Generation .
I will talk about this method using the example of a task that is somewhat more general than the problem of triangulations: we will generate all the “cuts”, that is, the ways to split a polygon are not necessarily triangles, but polygons with a number of sides from the list that is input the program.
In order to describe this method we need several formal definitions.
Let X be some set of “structures”. Elements of the set X will be called labeled objects . In our task, the marked objects are cuts whose vertices are numbered counterclockwise. The data structure for tagged cuts is simple - these are adjacency lists:
public class Dissection { private int[][] adjacent; ... } Let G be some permutation group acting on a set X. This means that each labeled object x from X and each element g of group G are assigned another labeled object y = g * x, and the following properties are true:
- Multiplying any elements of the group h and g corresponds to the sequential application of actions to the object x: h * (g * x) = (hg) * x.
- The unit of the group e translates each tagged object x into itself: e * x = x.
It can be shown that the whole set X is divided into equivalence classes of the relative relation: x and y are equivalent if x = g * y. In our first example with triangulations, the elements of the group — turns by 0, 60, 120, 180, 240, and 300 degrees — divide the whole set into four equivalence classes, whose elements differ precisely in their structure, and not in the marks of the vertices. These equivalence classes were depicted in the second figure. We will call these classes unlabeled objects .
To each element of X, we associate a natural number, which we will call order. The order of all equivalent objects must be the same. This property allows you to further define the order for equivalence classes (unlabeled objects): it will be equal to the order of any representative of the corresponding class. For our example in the figure, the order is the number of vertices in the polygon. All unlabeled objects in the figure are six.
These were fairly general definitions. We now turn to definitions specific to the future algorithm. To each marked object x, we associate two sets — the set of lower objects L (x) and the set of upper objects U (x). The orders of the elements in these sets are by definition equal to the order of x. Before giving formal requirements for lower and upper objects, I will try to give an intuitive description. Each lower object must contain information about how to uniquely move from the current object to an object of a smaller order. For example, a lower dissection object is a dissection in which one of the "extreme" polygons is additionally highlighted (for example, colored red), which can be cut off from this dissection. The upper object is, on the contrary, the marked object plus information, allowing it to unambiguously “increase” it by increasing the order. The upper dissection, for example, is a dissection in which one of the sides of the polygon is additionally highlighted (for example, colored red) and a number is written on it. Looking at this cut, we can figure out which side to glue the new polygon to increase the order. The number of sides of the glued polygon will be determined by what number is written on the edge. This idea can be illustrated by the following figure, depicting two objects - the lower and the upper, corresponding to the same dissection.
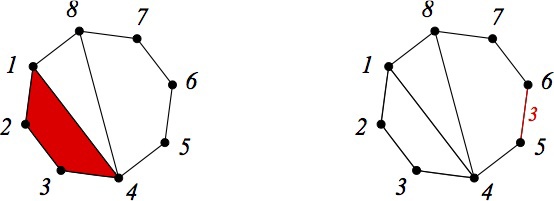
In the program, the lower and upper cuts are presented as follows:
public class LowerDissection { private Dissection dissection; private int after; ... } public class UpperDissection { private Dissection dissection; private int after, size; ... } For the lower dissection, we store only the number of the vertex from which the polygon begins, which we are going to delete. For the top cut, the number of the vertex is stored, after which it will be necessary to paste a new polygon, as well as the number of its sides.
You can see that some of the lower and upper objects are in the relation of "correspondence": the lower object corresponds to the upper one, which is obtained after we reduced the order in the manner encoded in the lower object.

Here the top object is mapped to the lower object, the result of deleting the selected quadrilateral. In the following picture - the opposite: a pentagon is glued to the top object, or rather, to its highlighted edge with the five written on it. This results in a lower object that stores information on how to roll back the operation performed.

Now, formally, what do you need to require from the mentioned structures:
- The group G acts on three types of objects: marked, upper and lower. Each of these three sets is closed with respect to the group action (this means that, for example, by acting on the lower object with an element of the group, we cannot get the upper one — a rather formal requirement).
- For each tagged object x and an element of the group g: L (g * x) = g * L (x); U (g * x) = g * U (x) (the notation g * L (x) means that we apply g to each element of the set L (x), similarly for g * U (x)).
- For each lower object y, the corresponding set of upper objects is not empty.
- If the two lower objects y and x are equivalent (that is, y = g * x), then any two corresponding upper objects are also equivalent.
- If the two upper objects y and x are equivalent, then any two corresponding lower objects are also equivalent.
- The order of the lower object is greater than the order of any corresponding upper one.
To better understand this concept, I suggest you distract from reading for a moment and think about what the lower and upper objects will look like if you take graphs without triangles as X (that is, graphs in which no three vertices are connected by edges all at once ).
Answer
Of course, this is not the only way, but it is quite natural to take graphs without triangles as lower objects, in which one of the vertices is colored red (this will mean that we are going to delete it), and as the upper ones - graphs without triangles, which several vertices are painted red (this will mean that we are going to add a vertex and connect it with all the red vertices). At the same time, it is necessary to require that the red vertices are not connected in pairs. In this case, after adding a new vertex, triangles are not formed.
We continue. Let nothing can be “bitten off” from some unlabeled object. Thus, there are no lower objects corresponding to it (or rather, corresponding to its marked objects). Such an object is called irreducible . In our case, irreducible are dissections consisting of a single polygon. All others are reducible .
Our algorithm will generate all non-isomorphic cuts sequentially, starting with irreducible ones, gradually increasing their order. To do this, we will paste all possible polygons from all possible sides to the current section. The problem, however, is that one can come to the same dissection in several ways. For example, you can come to the cut of the octagon, which corresponded to the lower object in the two previous pictures, by gluing a quadrilateral to a triangle, and then a pentagon, or by gluing, on the contrary, a triangle and a quadrilateral to a pentagon. Thus, it is possible to generate the same dissection several times, and not even notice it. This is what you just want to avoid.
To get around this problem by generating a new dissection, we will check if it is true that the last addition of the polygon corresponds to some single canonical way of constructing this dissection. To do this, we need the function P, which associates with each marked object a set of lower objects for which it is a “descendant”. The function P must meet the following requirements:
- If L (x) is empty, then P (x) is also empty.
- If L (x) is not empty, then P (x) consists of such and only those corresponding to the object x lower objects that any two of them are transformed into each other under the action of some element g for which g * x = x.
- For any unlabeled object x and element of the group g: g * P (x) = P (g * x).
It is worth paying special attention to the second requirement: it, in fact, means that the set P (x) must consist of several objects that are equivalent with respect to the symmetries of the object x. Suppose, for example, it turned out that the dissection of x is symmetrical about only turns to 0 and 180 degrees. Then P (x) must consist of exactly two lower objects, obtained from each other by means of such turns.
Let's try to satisfy the general requirement in our example. To do this, take some dissection x and scroll through it marks all n ways (n is the number of vertices). Every time when the “extreme” polygon starts from the vertices 1 and 2 (such that it can be cut off), we will remember this numbering. After that, from all the selected vertex numbering options, choose those that give a lexicographically minimal (any other reasonable order) the adjacency list entry. These numbering allocates us some polygons on the source object x - those that, with appropriate numbering, start with 1 and 2. P (x) just consists of lower objects for x, in which these polygons are colored red. You can't do without a picture:

So, we chose the cut x, shown on the left, and rearranged the marks in eight different ways. The methods a, c, e and g do not immediately suit us: on the vertices 1,2, ..., i, there is no polygon that can be cut off. It can be seen that methods b and f are essentially the same, as are methods d and h. Of these four methods, choose those that are in some sense "minimal." As we have already noticed, you can define at least as you like, but definitely. For example, a minimal lexicographically record of adjacency lists is appropriate. In this case, methods b and f win. This method gives us triangles 2,3,4 and 6,7,8 on the original tagged object x. As a result, we get the two lower objects shown in the figure on the right.
The P function is the most important for fast generation. To meet these requirements and maintain high speed, in fact, it is very difficult. As can be seen, the function P, in a certain sense, allows us to indicate which of the ways to “bite off” the extreme polygon is canonical, up to isomorphism. If the concept is clear, I suggest you figure out how the P (x) function should work for the already mentioned graphs without triangles.
Answer
The answer, of course, is not straightforward. One of the simple (but not very efficient) methods is as follows: for a graph without triangles, x will iterate over all ways to renumber the vertices, and then leave those that lexicographically minimally write adjacency lists. For each of these methods, choose the vertex v having the number 1 and compose the lower object - the graph x with the vertex v colored red. All such different lower objects form the result of the work P (x).
The code that adds to the classes described above methods that implement all of these functions, it is better to look in the repository : it has too many technical details to discuss it in detail.
Now everything is ready to describe directly the generation algorithm. It will run for every irreducible cut. For the current dissection, we consider all non-isomorphic ways to create the top object, and then we increment each resulting top object to the bottom with increasing order. Further, using the P function, we check every lower object for the fact that it is indeed the parent of the corresponding marked object. If this check passes, then we consider that this tagged object is a representative of a new equivalence class; we run the algorithm for it recursively. You can, of course, prove the correctness of this algorithm, but I feel that I already overdid it a little with formalism, and in order to deal with the evidence, it is easier to refer to the original article .
Better let's look first at the code responsible for generating:
public static void generateSubtreeFrom(Dissection root, int maxOrder) { for (UpperDissection upper : root.createAllUpper()) { LowerDissection lower = upper.createArbitraryLower(); if (lower != null) { Dissection probableChild = lower.getUnderlyingDissection(); if (probableChild.getOrder() <= maxOrder && lower.isParentFor(probableChild)) { root.addChild(probableChild); generateSubtreeFrom(probableChild, maxOrder); } } } } And now for the result of generating all non-isomorphic cuts into 3.4 and 5-gons, up to an order equal to eight. Arrows are directed from parents to descendants. It can be seen that all the dissections formed trees whose roots are irreducible objects.

The source code of the program that generated this image is available in google code . The result of her work is a description in graphviz format.
In conclusion, I will add that for the considered problem, in principle, one can come up with a simpler and faster algorithm. However, the described procedure is applicable to almost all types of combinatorial objects that can be constructed in an inductive way, “building up” the structure. Moreover, for some types of graphs, at least, according to the author of the algorithm, this approach provides some of the best, if not the best, generation rates today.
Source: https://habr.com/ru/post/225255/
All Articles