New invariant number. The study of the natural number series (NPS)
In the arithmetic of natural numbers, it is sometimes necessary to find the divisors of the composite number N. The simple operation, the inverse of the multiplication of numbers, is currently unknown. Its absence creates certain difficulties in solving some practical problems, especially if you have to manipulate with numbers of high and very high capacity (hundreds or even thousands of numbers representing numbers).
In the work “The Fundamental Structures of the Natural Series of Numbers” AE Vaulin, S.V. Pilkevich - Intellectual Systems. Proceedings of the Seventh International Symposium. Ed. K.A. Pupkova. - Moscow: RUSAKI, 2006. - p. 384-387. Provides information about the original concept of modeling a natural number of numbers and an individual number in order to establish properties that are weakly dependent or not at all dependent on the digit capacity of numbers. Further development and refinement of the details of this approach is the subject of this paper.
The independence of some properties of numbers from their digit capacity was one of the main ideological premises of the proposed analytical approach to the modeling of numbers. The presence of such properties in numbers confirms the existence of signs of divisibility of numbers. For example, no matter what value a given number is, if the convolution (sum) of its digits is divided by three, then the original number is divided by three. The divisibility by three is practically independent of the digit capacity. Similarly for other signs of divisibility. This is evidence that some properties of numbers may not depend on their digit capacity. The search for such properties and the development of the theory of their use in various directions, in particular, in the development of factorization algorithms, the establishment of simplicity of a number, and other equally difficult problems is an important and important problem of modern mathematics.
')
The paper describes a newly discovered feature-property of numbers. This feature is useful for developing algorithms for solving both new and traditional problems of theory and practice. Let us first give the qualitative informative arguments about the essence of the proposed work.
Natural series . We will further consider the natural series of numbers as a mathematical object that has a complex structure. NPS can be considered as a set of different series with different properties, for example, composed of two arithmetic progressions of even and odd numbers. These progressions have the same difference d , equal to d = 2 , but with different initial elements: a = 1 for a progression of odd numbers and a = 2 for a progression of even numbers. Load all the numbers of the NPS in the cells (bits) of the register and then the NPS can be represented by a register with an infinite number of cells. Pay attention to a series of odd numbers.
In the NPS, we consider three adjacent consecutive numbers 2n – 1 , 2n , 2n + 1 , the average of which is even. Square them up. Between the squares of the extreme odd numbers, there is always an even number of digits of the 8k register, which is divided by an even square into two consecutive (adjacent) odd numbers of the form 4k – 1 on the left and 4k + 1 on the right. The cell of the even-numbered square belongs to the right number.

Thus, any odd number of the form N = 4k ± 1 , k> 0 is an arbitrary positive integer, in the NPS always lies between the squares of the numbers N = x 1 2 –x 0 2 with different parity. In certain cells of the NGF squares of natural numbers are placed. This arrangement corresponds to a number of laws. Odd squares alternate with even squares. Moreover, if the larger square x 1 2 is even, then N = 4k – 1 and N≡3 (mod4) , and if the larger square x 1 2 is odd, then N = 4k + 1 and N≡1 (mod4) .
Imagine the register NRCH ruler with the engine as a logarithmic. For a given number N in the engine, we will create a window with the size of N + 1 positions (digits). By moving the slider along the NPSF ruler, we will find and fix its positions with a pair of numbers (x 0 2 , x 1 2 ) that are placed in the extreme positions of the window ( x 0 2 - left and x 1 2 - right) and both values will correspond to numeric squares. The difference between the squares in the extreme positions of the window will obviously coincide with the number N = x 1 2 –x 0 2 .
The contours of the NPS . The distance between the squares of two consecutive odd numbers is called the contour . The distance between cells with squares of non-adjacent numbers is called the interval in the NPS. If the sum of adjacent odd numbers is a multiple of 8 , then it forms the length of the interval, called the contour , and the value of k is the number of this contour. So the adjacent numbers 11 and 13 form a contour (11 + 13 = 24 = 3 • 8) with the number k = 3 and a length L (k) = 24 = k • 8 , and the adjacent odd numbers 13 and 15 do not form the contour (13+ 15 = 28 ≠ k • 8) .
The distances between the odd squares-boundaries of adjacent numbers always form outlines and contain the number of register cells equal to 8k . The contours in the NPS form a continuous sequence with the numbers k = 1 (1) ∞ , i.e. The NPS is formed by cells filled with numbers in a sequence of contours, whose lengths are multiples of 8 . The first circuit has the length L (1) = 3 2 –1 2 = 1 • 8 , the second circuit - L (2) = 5 2 –3 2 = 2 • 8 = 16 , and so on. The lengths of the contours form an arithmetic progression with the difference d = 8 and a = 8 .
Filling all window positions with numbers (intervals) in each of the fixed numbers (x 0 2 , x 1 2 ) positions has a regularity and is characterized by some numerical invariant established in the work. Since the pairs (x 0 2 , x 1 2 ) can be more than one, we will supply its numbers with the index i .
For N = 105 (window size - 1) there are 4 positions (4 pairs of squares of different parity), which are fixed. We will control the position of the left border of the window. Start moving the engine from 1 to the right. The first position (stop) occurs when the number x 0 2 = 4 appears on the left border of the window, but the right border is 109 - not a square, then on the left border of the window there is a square x 0 2 = 9 , but on the right the number 114 is not a square , after passing the position with the number 15 in the window on the left, the number x 0 2 = 16 appears - a square. We stop and check the number on the right border of the window. There we see the number x 1 2 = 121 - also a square. We fix this position with the control of the difference between the squares: x 11 2 –x 01 2 = 11 2 –4 2 = 105 .
We continue to move until the arrival of the left edge of the window at positions 25 , 36 , 49 and see that for them the right border does not fall on the square. But when the number 64 appears in the window to the left, on the right we see the number 169 - a square. We fix this position and perform the control x 12 2 –x 02 2 = 13 2 –8 2 = 105 .
The next fixed window position is: on the left, the number x 2 = 256 , and on the right, x 1 2 = 361 , both squares. We fix and control the difference between the squares x 13 2 –x 03 2 = 19 2 –16 2 = 105 .
And, finally, the fourth window position gives the difference of squares equal to x 14 2 –x 04 2 = 53 2 –52 2 = 105 .
Further movement stops, since there is no longer a pair of squares, the difference between which is equal to the number N = 105 , the difference of all pairs will be greater than 105 . The fourth pair x 14 2 , x 04 2 is called the limiting pair.

Semi-contours . The location of each even square of the form (2k) 2 in the inner cell of the k- th contour. This cell divides the length L (k) of the contour into two m (k) = 4k – 1 and M (k) = 4k + 1 adjacent odd numbers ( left and right ), called semi - contours . Note that contours and semi-contours are sets of cells filled with natural numbers, and m (k) and M (k) are the powers of these sets. The sets of cells of successively following half-contours form the NPS. The whole set of odd numbers form two classes: the left numbers N≡3 (mod4) and the right numbers N≡1 (mod4) . The lengths of the semi-contours of the first contour, the left odd number 4 • 1–1 = 3 and the right odd number 4 • 1 + 1 = 5 , together form the length L (k = 1) = 3 + 5 = 8 contours with the number k = 1 .
Border contour . For a given contour number k, it is completely determined, half-contours with length m (k) = 4k – 1 left and M (k) = 4k + 1 right, the boundaries of this contour left Gl (k) = (2k – 1) 2 and right (k) = (2k + 1) 2 . The contour length is L (k) = m (k) + M (k) = (k) – (k) = 8k . The even square (k) = (2k) 2 is the common border of semi-contours.
Indeed, the difference between the boundaries (k) – (k) = (2k + 1) 2 - (2k – 1) 2 =4k 2 + 2 • 2k + 1 - 4k 2 + 2 • 2k – 1 = 8k .
Limit contour . Any odd number N can be represented as a semi-contour in a certain contour with number k p . Such a contour is unique, since the contour to the left of the limiting one has semi-contours smaller N , and to the right - large N. The number N, left or right, is determined using the even square of the limiting contour. For the left N = x 1 2 –x 0 2 , and x 1 is even, for the right N = x 1 2 –x 0 2 and x 1 is odd. Here the role of the boundaries of the semi-contour is played by the values x 1 2 and x 0 2 . These boundaries are determined from the expressions x 1 = (N + 1) / 2 and x = (N – 1) / 2 . The length of the limit circuit with the number k p for the number N is determined by the formula
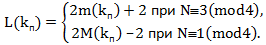
The number k n of the limit contour of the number N is calculated through the length of the limit contour k n = L (k n ) / 8 . Now is the time to clarify the concepts introduced by a numerical example. This is a specially selected example, very simple, contributing to a better understanding of the phenomenon under study.
Let a composite odd natural number (snnch)N = 105 = 3 • 5 • 7 be given . For this number, it is required to find the limit contour, its boundaries and determine its number k n . Specify all pairs of squares (x i1 2 , x i0 2 ) , i = 1 (1) ... of different parity, the difference between which is equal to the number N = 105 .
Decision. For better assimilation of the content of the example, it is recommended to use a pencil and paper. It is known that snnch lies between the squares of different parityN = x 1 2 –x 0 2 . We define the left or right number given by N = 105≡1 (mod4) . The number N is right, i.e. it is a larger semi-circuit in the marginal contour. We define the boundaries of the limit contour using the value N , x 1 = (N + 1) / 2 = (105 + 1) / 2 = 53 and x = (N – 1) / 2 = (105–1) / 2 = 52 . The squares of the numbers 52 and 53 are the boundaries of the semi-contour.
The length of the contour isL (kn) = 2 • 105–2 = 208 = 8 • kn , from which kn = 208/8 = 26 . The smaller (left) semi-contour has a length m (kn) = L (kn) –M (kn) = 208–105 = 103 , is a prime number.
We find through k p the boundaries of the limit contour: the leftG l (k p ) = (2k n –1) 2 = (2 • 26–1) 2 = 51 2 = 2601 and the right G n (k n ) = (2k n + 1) 2 = (2 • 26 + 1) 2 = 53 2 = 2809 . The length of the contour through its boundaries is determined by the expression L (k p ) = G p (k p ) –G l (k p ) = 2809–2601 = 208 = 8k p .
Since the given snnch N = 105 is a semi-contour in the limit circuit, we will assume that only half of the number of the limit contour corresponds to it, i.e.k p (N) / 2 = 26/2 = 13 .
Invariant number . The characteristic of the number N in the form of kn (N) / 2 is called the invariant of the number N , and then we will show why this name is chosen. The invariant can be an integer or a fractional number depending on the parity of the number k n of the limit contour.
NPSH intervals for the number N. Next, we consider the possibility of representing the sn = N = 105 difference of other pairs of squares of different parity. The number 105 , as well as any other odd number, can be represented as a sum of an odd number of smaller adjacent odd numbers. The usefulness of such a representation of N follows from the fact that the boundaries of all odd numbers in the NPST are squares, therefore, the continuous interval representing N = 105 of adjacent odd numbers will have squares on the boundaries. The number of items in the sum must be an odd number.
The considered example shows that for the number N = 105 there are four pairs of squares of different parity, the distance in the NPS between them is 105. Each of the pairs of squares found solves the problem of factorization sn = N = 105 , excluding the limiting pair - it gives a trivial factorization.
It remains an open very important question, where to take, how to get for an arbitrary number N of a pair(x o 2 , x 1 2 ) squares?
An analysis of the results of Example 2 shows that different pairs of squares(x i 2 , x 1i 2 ) , i = 1 (1) 4 , are obtained with different representations of the invariant kn (N) / 2 = 13 as a sum with a different number of terms. Such sums themselves can be considered as splittings of the number 13 of a special form. All terms of the sum are a segment of the NPS in which one of the extreme terms in the sum is included only in its half. The definition of such a term is dictated by the belonging of the number N to the class of left or right odd numbers.
If N is left, then half is taken from the larger term:
If N is right, then half is taken from the smaller term:
Thus, from the considered facts there follows an algorithm for solving the problem of factoring numbers:
The considered material allows to draw the following conclusions.
In the work “The Fundamental Structures of the Natural Series of Numbers” AE Vaulin, S.V. Pilkevich - Intellectual Systems. Proceedings of the Seventh International Symposium. Ed. K.A. Pupkova. - Moscow: RUSAKI, 2006. - p. 384-387. Provides information about the original concept of modeling a natural number of numbers and an individual number in order to establish properties that are weakly dependent or not at all dependent on the digit capacity of numbers. Further development and refinement of the details of this approach is the subject of this paper.
The independence of some properties of numbers from their digit capacity was one of the main ideological premises of the proposed analytical approach to the modeling of numbers. The presence of such properties in numbers confirms the existence of signs of divisibility of numbers. For example, no matter what value a given number is, if the convolution (sum) of its digits is divided by three, then the original number is divided by three. The divisibility by three is practically independent of the digit capacity. Similarly for other signs of divisibility. This is evidence that some properties of numbers may not depend on their digit capacity. The search for such properties and the development of the theory of their use in various directions, in particular, in the development of factorization algorithms, the establishment of simplicity of a number, and other equally difficult problems is an important and important problem of modern mathematics.
')
The paper describes a newly discovered feature-property of numbers. This feature is useful for developing algorithms for solving both new and traditional problems of theory and practice. Let us first give the qualitative informative arguments about the essence of the proposed work.
Natural series . We will further consider the natural series of numbers as a mathematical object that has a complex structure. NPS can be considered as a set of different series with different properties, for example, composed of two arithmetic progressions of even and odd numbers. These progressions have the same difference d , equal to d = 2 , but with different initial elements: a = 1 for a progression of odd numbers and a = 2 for a progression of even numbers. Load all the numbers of the NPS in the cells (bits) of the register and then the NPS can be represented by a register with an infinite number of cells. Pay attention to a series of odd numbers.
In the NPS, we consider three adjacent consecutive numbers 2n – 1 , 2n , 2n + 1 , the average of which is even. Square them up. Between the squares of the extreme odd numbers, there is always an even number of digits of the 8k register, which is divided by an even square into two consecutive (adjacent) odd numbers of the form 4k – 1 on the left and 4k + 1 on the right. The cell of the even-numbered square belongs to the right number.

Thus, any odd number of the form N = 4k ± 1 , k> 0 is an arbitrary positive integer, in the NPS always lies between the squares of the numbers N = x 1 2 –x 0 2 with different parity. In certain cells of the NGF squares of natural numbers are placed. This arrangement corresponds to a number of laws. Odd squares alternate with even squares. Moreover, if the larger square x 1 2 is even, then N = 4k – 1 and N≡3 (mod4) , and if the larger square x 1 2 is odd, then N = 4k + 1 and N≡1 (mod4) .
Imagine the register NRCH ruler with the engine as a logarithmic. For a given number N in the engine, we will create a window with the size of N + 1 positions (digits). By moving the slider along the NPSF ruler, we will find and fix its positions with a pair of numbers (x 0 2 , x 1 2 ) that are placed in the extreme positions of the window ( x 0 2 - left and x 1 2 - right) and both values will correspond to numeric squares. The difference between the squares in the extreme positions of the window will obviously coincide with the number N = x 1 2 –x 0 2 .
The contours of the NPS . The distance between the squares of two consecutive odd numbers is called the contour . The distance between cells with squares of non-adjacent numbers is called the interval in the NPS. If the sum of adjacent odd numbers is a multiple of 8 , then it forms the length of the interval, called the contour , and the value of k is the number of this contour. So the adjacent numbers 11 and 13 form a contour (11 + 13 = 24 = 3 • 8) with the number k = 3 and a length L (k) = 24 = k • 8 , and the adjacent odd numbers 13 and 15 do not form the contour (13+ 15 = 28 ≠ k • 8) .
The distances between the odd squares-boundaries of adjacent numbers always form outlines and contain the number of register cells equal to 8k . The contours in the NPS form a continuous sequence with the numbers k = 1 (1) ∞ , i.e. The NPS is formed by cells filled with numbers in a sequence of contours, whose lengths are multiples of 8 . The first circuit has the length L (1) = 3 2 –1 2 = 1 • 8 , the second circuit - L (2) = 5 2 –3 2 = 2 • 8 = 16 , and so on. The lengths of the contours form an arithmetic progression with the difference d = 8 and a = 8 .
Filling all window positions with numbers (intervals) in each of the fixed numbers (x 0 2 , x 1 2 ) positions has a regularity and is characterized by some numerical invariant established in the work. Since the pairs (x 0 2 , x 1 2 ) can be more than one, we will supply its numbers with the index i .
Example 1
For N = 105 (window size - 1) there are 4 positions (4 pairs of squares of different parity), which are fixed. We will control the position of the left border of the window. Start moving the engine from 1 to the right. The first position (stop) occurs when the number x 0 2 = 4 appears on the left border of the window, but the right border is 109 - not a square, then on the left border of the window there is a square x 0 2 = 9 , but on the right the number 114 is not a square , after passing the position with the number 15 in the window on the left, the number x 0 2 = 16 appears - a square. We stop and check the number on the right border of the window. There we see the number x 1 2 = 121 - also a square. We fix this position with the control of the difference between the squares: x 11 2 –x 01 2 = 11 2 –4 2 = 105 .
We continue to move until the arrival of the left edge of the window at positions 25 , 36 , 49 and see that for them the right border does not fall on the square. But when the number 64 appears in the window to the left, on the right we see the number 169 - a square. We fix this position and perform the control x 12 2 –x 02 2 = 13 2 –8 2 = 105 .
The next fixed window position is: on the left, the number x 2 = 256 , and on the right, x 1 2 = 361 , both squares. We fix and control the difference between the squares x 13 2 –x 03 2 = 19 2 –16 2 = 105 .
And, finally, the fourth window position gives the difference of squares equal to x 14 2 –x 04 2 = 53 2 –52 2 = 105 .
Further movement stops, since there is no longer a pair of squares, the difference between which is equal to the number N = 105 , the difference of all pairs will be greater than 105 . The fourth pair x 14 2 , x 04 2 is called the limiting pair.

Semi-contours . The location of each even square of the form (2k) 2 in the inner cell of the k- th contour. This cell divides the length L (k) of the contour into two m (k) = 4k – 1 and M (k) = 4k + 1 adjacent odd numbers ( left and right ), called semi - contours . Note that contours and semi-contours are sets of cells filled with natural numbers, and m (k) and M (k) are the powers of these sets. The sets of cells of successively following half-contours form the NPS. The whole set of odd numbers form two classes: the left numbers N≡3 (mod4) and the right numbers N≡1 (mod4) . The lengths of the semi-contours of the first contour, the left odd number 4 • 1–1 = 3 and the right odd number 4 • 1 + 1 = 5 , together form the length L (k = 1) = 3 + 5 = 8 contours with the number k = 1 .
Border contour . For a given contour number k, it is completely determined, half-contours with length m (k) = 4k – 1 left and M (k) = 4k + 1 right, the boundaries of this contour left Gl (k) = (2k – 1) 2 and right (k) = (2k + 1) 2 . The contour length is L (k) = m (k) + M (k) = (k) – (k) = 8k . The even square (k) = (2k) 2 is the common border of semi-contours.
Indeed, the difference between the boundaries (k) – (k) = (2k + 1) 2 - (2k – 1) 2 =
Limit contour . Any odd number N can be represented as a semi-contour in a certain contour with number k p . Such a contour is unique, since the contour to the left of the limiting one has semi-contours smaller N , and to the right - large N. The number N, left or right, is determined using the even square of the limiting contour. For the left N = x 1 2 –x 0 2 , and x 1 is even, for the right N = x 1 2 –x 0 2 and x 1 is odd. Here the role of the boundaries of the semi-contour is played by the values x 1 2 and x 0 2 . These boundaries are determined from the expressions x 1 = (N + 1) / 2 and x = (N – 1) / 2 . The length of the limit circuit with the number k p for the number N is determined by the formula
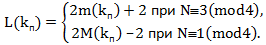
The number k n of the limit contour of the number N is calculated through the length of the limit contour k n = L (k n ) / 8 . Now is the time to clarify the concepts introduced by a numerical example. This is a specially selected example, very simple, contributing to a better understanding of the phenomenon under study.
Example 2
Let a composite odd natural number (snnch)
Decision. For better assimilation of the content of the example, it is recommended to use a pencil and paper. It is known that snnch lies between the squares of different parity
The length of the contour is
We find through k p the boundaries of the limit contour: the left
Since the given snnch N = 105 is a semi-contour in the limit circuit, we will assume that only half of the number of the limit contour corresponds to it, i.e.
Invariant number . The characteristic of the number N in the form of kn (N) / 2 is called the invariant of the number N , and then we will show why this name is chosen. The invariant can be an integer or a fractional number depending on the parity of the number k n of the limit contour.
NPSH intervals for the number N. Next, we consider the possibility of representing the sn = N = 105 difference of other pairs of squares of different parity. The number 105 , as well as any other odd number, can be represented as a sum of an odd number of smaller adjacent odd numbers. The usefulness of such a representation of N follows from the fact that the boundaries of all odd numbers in the NPST are squares, therefore, the continuous interval representing N = 105 of adjacent odd numbers will have squares on the boundaries. The number of items in the sum must be an odd number.
- Suppose that there are three such terms. Obviously, 105: 3 = 35 and the first term will be 35–2 = 33 , the second 35 , and the third 35 + 2 = 37 . Numbers 33 , 35 , 37 form a continuous sequence of odd adjacent numbers, and 35 and 37 are half-contours of one circuit, since their sum is 35 + 37 = 72 times 8 . This circuit has the number k = 72/8 = 9 . The number 33 belongs to another previous contour with the number k = 8 and is right in it, i.e. great. This number 33 corresponds to half the number of its contour, i.e. k / 2 = 8/2 = 4 . The interval of three odd numbers adjacent to each other with a length of 105 cells in the NFC corresponds to the sum of the contour numbers in the form of kn (N) / 2 = 8/2 + 9 = 4 + 9 = 13 .
For this interval, we define the boundaries. The large boundary of the interval coincides with the right boundary of the larger contour with the number k = 9 , i.e. (k) = (2 • k + 1) 2 = (2 • 9 + 1) 2 = 19 2 = x 1 2 = 361 . The smaller boundary of the interval coincides with the left boundary of the smaller of the three semi-circuits, i.e. the numbers 33 in the contour with the number k = 8 , its boundary is the even square of the double contour number (k) = (k) = (2k) 2 = (2 • 8) 2 = x 0 2 = 256 . Check: N = (9) – (8/2) = 361–256 = 105 .
Now for N = 105 we can write the factors N = x 1 2 –x 0 2 = (19 + 16) (19–16) = 35 • 3 = 105 . - Let the representation of N have half-contours in the sum of five odd terms. Obviously, 105: 5 = 21 and the first term will be 21–4 = 17 , the second 21–2 = 19 , the third 21 , the fourth 21 + 2 = 23 and, finally, the fifth 21 + 4 = 25 . Numbers 17 , 19 , 21 , 23 , 25 form a continuous sequence of odd adjacent numbers, and 19 , 21 and 23 , 25 of them are half-contours of two adjacent contours, since their sum is 19 + 21 = 40 = 5 • 8 and 23 + 25 = 48 = 6 • 8 is a multiple of 8 . These contours are numbered k = 40/8 = 5 and k = 48/8 = 6 .
The number 17 is the large (right) semi-contour of the preceding contour with the number k = (15 + 17) / 8 = 4 . This number corresponds to half the number of the smaller contour k / 2 = 4/2 = 2 . The interval of five odd numbers adjacent to each other with a length of 105 cells in the NPST corresponds to the sum of the contour numbers kn (N) / 2 = 4/2 + 5 + 6 = 2 + 5 + 6 = 13 .
For this interval, we define the boundaries. The large boundary of the interval coincides with the right boundary of the larger contour with the number k = 6 , i.e. (k) = (2 • k + 1) 2 = (2 • 6 + 1) 2 = 13 2 = x 1 2 = 169 . The smaller left border of the interval coincides with the left border of the smaller semi-circuit, i.e. the number 17 , located in the contour with the number k = 4 . The smaller boundary is the even square of the double contour number (k) = (k) = (2k) 2 = (2 • 4) 2 = x 0 2 = 64. Checking for the difference of squares: N = (6 ) –Gh (4) = 169–64 = 105 . Now for N = 105 we can write the factors N = x 1 2 –x 0 2 = (13 + 8) (13–8) = 21 • 5 = 105 . - Let the sum of the sum representing the number N be seven. Obviously, 105: 7 = 15 and the first term will be 15–6 = 9 , the second 15–4 = 11 , the third 15–2 = 13 , the fourth 15 , the fifth 15 + 2 = 17 , the sixth 15 + 4 = 19 and, finally, the seventh 15 + 6 = 21 . Numbers 9 , 11 , 13 , 15 , 17 , 19 , 21 form a continuous sequence of odd adjacent numbers, and 11, 13 ; 15, 17 and 19, 21 are half-contours of three adjacent contours, since their sums are 11 + 13 = 24 = 3 • 8 ; 15 + 17 = 32 = 4 • 8 and 19 + 21 = 40 = 5 • 8 multiples of 8 . These outlines have the numbers k = 24/8 = 3 , k = 32/8 = 4 and k = 40/8 = 5 .
The number 9 is the large (right) semi-contour of the preceding contour with the number k = (7 + 9) / 8 = 2 . This number corresponds to half the number of the smaller contour, i.e. k / 2 = 2/2 = 1 . The interval of seven odd numbers adjacent to each other with a length of 105 cells in the NPSF corresponds to the sum of the contour numbers kn (N) / 2 = 2/2 + 3 + 4 + 5 = 1 + 3 + 4 + 5 = 13 .
For this interval, we define the boundaries. The large boundary of the interval coincides with the right boundary of the larger contour with the number k = 5 , i.e. (k) = (2 • k + 1) 2 = (2 • 5 + 1) 2 = 11 2 = x 1 2 = 121 . The smaller border of the interval coincides with the left border of the smaller semi-circuit, i.e. the number 9 located in the contour with the number k = 2 is the even square of the double contour number (k) = (k) = (2k) 2 = (2 • 2) 2 = x 0 2 = 16. Check: N = (5) – h (2) = 121–16 = 105 .
Now for N = 105 we can write the factors N = x 1 2 –x 0 2 = (11 + 4) (11–4) = 15 • 7 = 105 .
The considered example shows that for the number N = 105 there are four pairs of squares of different parity, the distance in the NPS between them is 105. Each of the pairs of squares found solves the problem of factorization sn = N = 105 , excluding the limiting pair - it gives a trivial factorization.
It remains an open very important question, where to take, how to get for an arbitrary number N of a pair
An analysis of the results of Example 2 shows that different pairs of squares
If N is left, then half is taken from the larger term:
- N = 183 is the left odd, 183≡3 (mod4) , half is taken from the larger term in the invariant representation by the sum k n (183) / 2 = 23 = 15 + 16/2 ; invariant integer;
- N = 203 is the left odd, 203≡3 (mod4) , half is taken from the larger term in the invariant representation with the sum k n (203) /2=25.5=6+7+8+9/2 ; the invariant is not an integer;
If N is right, then half is taken from the smaller term:
- N = 213 - right odd, 213≡1 (mod4) , half is taken from the smaller term in the invariant representation with the sum k n (213) /2=26.5=17/2+18 ; the invariant is not an integer;
- N = 217 - right odd, 217≡1 (mod4) , half is taken from the smaller term in the invariant representation with the sum k n (217) / 2 = 27 = 6/2 + 7 + 8 + 9 ; invariant integer;
Thus, from the considered facts there follows an algorithm for solving the problem of factoring numbers:
- For a given snnch N find the invariant k n / 2 .
- The invariant is presented by splitting a special type k n / 2 = a + ( a +1) + ( a + 2) + ... + ( a + t-1) + k d / 2 , where k d is the additional number of the extreme contour, left or right.
- For the extreme terms, calculate the boundaries: left Tl = x 0 2 and right Tn = x 1 2 .
- The boundary difference is represented by the product of brackets N = x 1 2 –x 0 2 = (x 1 + x 0 ) (x 1 – x 0 ) = pq .
The considered material allows to draw the following conclusions.
- The model of a composite odd natural number represented in terms of contours — the semi-contours of an NFC allows us to establish an invariant of such a number as a function of the numbers representing the number of contours. The invariant kn (N) / 2 saves the value, regardless of which pair of squares (if there are several pairs of squares) is represented as Sn = N = x i1 2 –x i0 2 , i = 1 (1) t , where t is the number of representing pairs . N = 105 = x i1 2 –x i0 2 = 53 2 –52 2 = 19 2 –16 2 = 13 2 –8 2 = 11 2 –4 2
- The value of the invariant is set by the elementary processing of a given number N when determining the number of the limit contour. The invariant can be either integer or fractional. Regarding the limit contour, theorems are formulated and proved, which are not given in the post, but are used.
- The proposed model of NPS in terms and concepts of contours - semi-contours opens up the possibility of formulating and studying the problem of factorizing odd numbers in a reasonable time for practical applications.
Source: https://habr.com/ru/post/225175/
All Articles